
Muy buenas a todos y todas, me he atrevido a resolver otra M2 para ustedes, espero que les sirva, en esta resolución nuevamente incluyo el paso a paso de los ejercicios, sin embargo, suelo omitir algunas explicaciones que considero algo obvias, de tener cualquier duda o sugerencia no duden en escribirme en los comentarios. Espero de corazón que les sea de utilidad.
P1

Solución:
Para resolver tendremos claramente identificado el punto de inicio 255 al cual iremos restando según indique cada medicamento.
En primer lugar debemos determinar cuánto debemos bajar el nivel de colesterol hasta llegar al riesgo medio, es decir, la diferencia entre el colesterol inicial con el limite del rango de riesgo medio. Esto es
\[255-240=15\]
es decir, con el primer medicamento debemos reducir 15\(\frac{mg}{dL}\)
Para determinar el tiempo que tardará este medicamento en reducir esa cantidad podemos hacer una división:
\[\frac{15}{2.5}\]
Es así como el primer descenso hasta riesgo medio queda modelado como:
\[\frac{255-240}{2,5}\]
El proceso con el segundo medicamento es similar,
Hacemos la diferencia entre los rangos de riesgo medio y riesgo bajo
\[240-200=40\]
Y ahora dividimos entre el aporte del segundo medicamento, resultando la expresión
\[\frac{240-200}{0.8}\]
Si sumamos ambos tiempos la expresión será
\[\frac{255-240}{2.5}+\frac{240-200}{0.8}\]
Letra E.
P2

Solución:
Podemos descartar las alternativas rápidamente si encontramos los números que conviertan esta expresión en un número entero,
\[n=1\to P=\frac{1-1}{1+1}=\frac{0}{2}=0\]
\[n=0\to P=\frac{0-1}{0+1}=\frac{-1}{1}=-1\]
\[n=-2\to P=\frac{-2-1}{-2+1}=\frac{-3}{-1}=3\]
\[n=-3\to P=\frac{-3-1}{-3+1}=\frac{-4}{-2}=2\]
Hasta este punto llevamos 4 valores, veamos que ocurre con algunos otros datos
\[n=-4\to P=\frac{-4-1}{-4+1}=\frac{-5}{-3}\]
\[n=-5\to P=\frac{-5-1}{-5+1}=\frac{-6}{-4}\]
De aquí en adelante mantendremos dos unidades de distancia entre numerador y denominador no pudiendo dividir de forma entera los números. Si probamos con los positivos que siguen ocurre lo mismo
\[n=2\to P=\frac{2-1}{2+1}=\frac{1}{3}\]
En este caso siempre obtendremos fracciones propias.
Letra C.
P3

Solución:
Iniciemos comentando que la diagonal (d) de un cuadrado se obtiene como: «la medida de su lado multiplicada por raíz de 2», es decir,
\[d=p\sqrt{2}\]
La diagonal del cuadrado B sería igual a
\[d_B=p\sqrt{2}\cdot \sqrt{2}=2p\]
La suma de ambas diagonales sería:
\[p\sqrt{2}+2p\]
En esta expresión debemos reemplazar las alternativas, para no hacerlo más extenso reemplazaré directamente la correcta
\[p\sqrt{2}+2p=\]
\[(\sqrt{2}-2)\sqrt{2}+2(\sqrt{2}-2)=\]
\[2-2\sqrt{2}+2\sqrt{2}-4=\]
\[2-4=-2\]
Letra D.
P4

Solución:
La clave para resolver aquí es entender quién es el 100%, en este caso es el porcentaje correspondiente a CHON, debemos sumar todos estos porcentajes para tener nuestro 100%, es decir,
\[18+10+65+3=96\]
También podíamos restar 100 – 4, :p.
Ahora procedemos a calcular el porcentaje mediante una proporción
\[\frac{65}{x}=\frac{96}{100}\]
\[\frac{65\cdot 100}{96}=x\]
\[\frac{65}{96}\cdot 100\]
Letra C.
P5
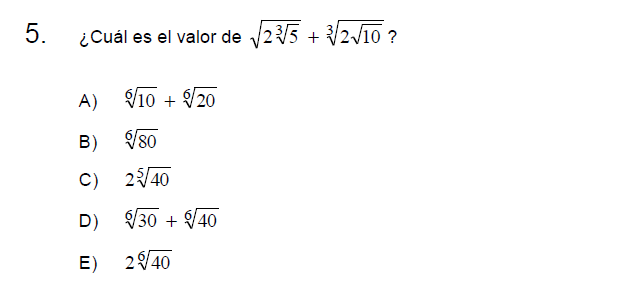
Solución:
Para resolver vamos a ingresar todos los términos en una sola raíz, es decir, ambos 2 serán ingresados y posteriormente aplicaremos raíz de una raíz:
\[\sqrt{2\sqrt[3]{5}}+\sqrt[3]{2\sqrt{10}}=\]
\[\sqrt{\sqrt[3]{2^35}}+\sqrt[3]{\sqrt{2^210}}=\]
\[\sqrt{\sqrt[3]{8\cdot5}}+\sqrt[3]{\sqrt{4\cdot10}}=\]
\[\sqrt{\sqrt[3]{40}}+\sqrt[3]{\sqrt{40}}=\]
\[\sqrt[6]{40}+\sqrt[6]{40}=\]
\[2\sqrt[6]{40}\]
Letra E.
P6

Solución:
Esta respuesta implica un contenido específico relacionado con valor absoluta en donde:
\[\sqrt{x^2}=|x|\]
con esto tenemos que
\[\sqrt{(a-b)^2}=|a-b|\]
Por lo tanto se nos pide que
\[|a-b|=a-b\]
Para que esto sea cierto necesariamente \(a>b\) de esta manera nos aseguramos que el resultado sea positivo en ambos lados de la ecuación, si \(b>a\) el resultado de la izquierda sería positivo y el de la derecha negativo. Es así que la alternativa correcta es C pues:
\[a-b>0\]
\[a>b\]
Letra C.
P7

Solución:
Para multiplicar raíces debemos tener necesariamente el mismo índice, por lo cual igualaremos ambos, transformando el índice 3 en 6, importante recordar que esto eleva también a la cantidad subradical (el 5):
\[\sqrt[6]{4}\cdot\sqrt[3]{5}=\]
\[\sqrt[6]{4}\cdot\sqrt[6]{5^2}=\]
\[\sqrt[6]{4}\cdot\sqrt[6]{25}=\]
\[\sqrt[6]{100}=\]
\[\sqrt[6]{10^2}=\]
Ahora simplificamos
\[\sqrt[3]{10}\]
Letra A.
P8

Solución:
En primer lugar vamos a separar la potencia de base 2
\[5^x \cdot 2^x \cdot 2^y\]
Ahora multiplicamos las potencias de igual exponente
\[10^x 2^y\]
Letra A.
P9

Solución:
Para determinar el punto correcto, debemos simplificar las expresiones de la segunda columna de la tabla, veamos uno por uno
Tras 1 hora:
\[2,5\cdot 10^2 \cdot (\frac{1}{2})^1=2,5 \cdot 5^2 \cdot 2^2 \cdot 2^{-1}\]
\[= 2,5 \cdot 5^2 \cdot 2\]
\[= 5 \cdot 5^2 \]
\[= 5^3 \]
Tras 2 horas:
\[2,5\cdot 10^2 \cdot (\frac{1}{2})^2=2,5 \cdot 5^2 \cdot 2^2 \cdot 2^{-2}\]
\[= 2,5 \cdot 5^2\]
Tras 3 horas:
\[2,5\cdot 10^2 \cdot (\frac{1}{2})^3=2,5 \cdot 5^2 \cdot 2^2 \cdot 2^{-3}\]
\[2,5 \cdot 5^2 \cdot 2^{-1} =\]
\[\frac{5}{2} \cdot 5^2 \cdot \frac{1}{2}\]
\[\frac{5^3}{4}\]
Tras 4 horas:
\[2,5\cdot 10^2 \cdot (\frac{1}{2})^4=2,5 \cdot 5^2 \cdot 2^2 \cdot 2^{-4}\]
\[\frac{5}{2}\cdot 5^2 \cdot \frac{1}{4} \]
\[\frac{5}{2}\cdot 5\cdot 5 \cdot \frac{1}{2} \cdot \frac{1}{2} \]
\[\frac{5}{2}\cdot \frac{5}{2}\cdot \frac{5}{2}\]
\[(\frac{5}{2})^3\]
\[2,5^3\]
Letra D.
P10

Solución:
Apliquemos la definición de log
\[log_3(0,\bar{1})=3^x=\frac{1}{9}\]
\[3^x=\frac{1}{3^2}\]
\[3^x=3^{-2}\]
\[x=-2\]
Letra E.
P11

Solución:
Para resolver este problema nos será de mucha utilidad recordar las fórmulas de altura y área de un triángulo equilátero:
altura:
\[\frac{lado \sqrt{3}}{2}\]
área:
\[\frac{lado^2 \sqrt{3}}{4}\]
y bueno, el área de este cuadrado será \(p^2\)
Usando la relación que nos otorga el enunciado podemos establecer que:
área del triángulo = un cuarto del área del cuadrado
\[\frac{q^2 \sqrt{3}}{4}=\frac{1}{4}p^2\]
\[\frac{q^2 \sqrt{3}}{4}=\frac{1}{4}p^2\]
\[4\cdot \frac{q^2 \sqrt{3}}{4}=p^2\]
\[q^2 \sqrt{3}=p^2\]
\[\sqrt{3}=\frac{p^2}{q^2}\]
Si aplicamos la raíz cuadrada nos quedará
\[\sqrt[4]{3}=\frac{p}{q}\]
\[3^{\frac{1}{4}}=\frac{p}{q}\]
Letra A.
P12

Solución:
Transformemos la expresión intentando utilizar los valores de la tabla
\[log35000=log 35\cdot 1000= log 7 \cdot 5\cdot 1000 =\]
\[log 7 \cdot 5\cdot 10^3=\]
\[log 7 + log 5 + log 10^3 =\]
\[log 7 + log 5 + 3log 10 =\]
\[0,845 + 0,699 + 3=\]
\[0,699 + 0,845 + 3\]
Letra C.
P13

Solución:
Para resolver utilizaremos la definición de logaritmo para expresar como potencias los log solicitados
\[log_p b = c \to p^c=b\]
y se nos pide determinar:
\[log_p \frac{1}{b}+ log_{\frac{1}{p}}b=\]
\[log_p \frac{1}{p^c}+ log_{\frac{1}{p}}p^c=\]
\[log_p p^{-c}+ log_{\frac{1}{p}}p^c=\]
\[log_p p^{-c}+ log_{\frac{1}{p}}(\frac{1}{p})^{-c}=\]
\[-c \cdot log_p p+ -c \cdot log_{\frac{1}{p}}\frac{1}{p}=\]
\[-c \cdot 1 + -c \cdot 1 =\]
\[-c + -c =\]
\[-2c\]
Letra A.
P14

Solución:
Debemos considerar que en el periodo de 50 días, la triplicación ocurrirá 5 veces, por este motivo la forma de modelar la situación debiera ser
\[\text{Cantidad inicial} \cdot 3^5=\]
\[8\cdot 10^5\cdot 3^5=\]
\[8\cdot 30^5\]
Letra A.
P15

Solución:
Podemos factorizar la expresión para comprenderla mejor
\[7^{46}-7^{44}=7^{44}(7^2-1)=\]
\[7^{44}\cdot 48\]
Podemos descartar la letra A, pues esta expresión es múltiplo de 2 \(\to 7^{44}\cdot 48 = 7^{44}\cdot 24 \cdot 2\)
Podemos descartar la letra B por la misma razón ya que puede ser dividida por 2.
Podemos afirmar que es múltiplo de 21, puesto que al descomponer el 48 obtenemos
\[7^{44}\cdot 3 \cdot 16 = 7^{43} \cdot 7\cdot 3 \cdot 16 =7^{43} \cdot 21 \cdot 16\]
Letra D.
P16

Solución:
Vamos reemplazando los datos en la fórmula
\[C=M(1+N)^n\]
\[C=2500000(1+N)^n\]
\[C=2500000(1+0,025)^n\]
En la expresión anterior el 2,5% se pasa a decimal dividiendo 2,5 en 100
\[C=2500000(1+0,025)^8\]
En la expresión anterior aparece un 8 ya que 1 año tiene 4 trimestres y luego 2 años tienen 8 trimestres.
\[C=2500000(1,025)^8\]
Letra B.
P17

Solución:
En primer lugar debemos entender que los descuentos se realizan sobre los 800.000 y luego de esto añadimos los 150.000, por lo cual descartamos A y B.
Ahora, la expresión con el 1 entre paréntesis debe indicar que multiplicamos los 800 mil por 1 obteniendo el total del cual vamos a descontar su porcentaje (17 + a)
Esto implica que la opción correcta es la letra C, la letra D incorpora el 1 dentro de los porcentajes (pues está dividido por 100)
Letra C.
P18

Solución:
La solución consiste en restar al área total (\(a^2\)) el área de ambos cuadrados (\(2p^2\)). Lo cual se puede escribir como una suma por su diferencia
\[a^2-2p^2=(a+\sqrt{2}p)(a-\sqrt{2}p)\]
Letra B.
P19

Solución:
Podríamos obtener la ecuación de la recta mediante dos puntos el (0,1) y el (90,10) utilizando la fórmula:
\[y-y_1=\frac{y_2-y_1}{x_2-x_1}(x-x_1)\]
\[y-1=\frac{10-1}{90-0}(x-0)\]
\[y-1=\frac{9}{90}(x)\]
\[y=\frac{1}{10}(x)+1\]
\[y=0,1x+1\]
Devolvemos las letras del problema
\[n(t)=0,1\cdot t +1\]
Letra D.
P20

Solución:
Dos variables son inversamente proporcionales cuando su producto es constante, según esta definición la primera tabla es la correcta, todas las multiplicaciones dan 40.
Letra A.
P21

Solución:
Las variables son directamente proporcionales, por lo tanto, su cociente es constante, podemos tomar un punto para establecer la proporción, por ejemplo, (300,171) (cada punto del eje X va de 50 en 50)
\[\frac{A}{S}=\frac{171}{300}\]
de aquí despejamos «S»
\[300A=171S\]
\[\frac{300A}{171}=S\]
\[\frac{100A}{57}=S\]
Letra C.
P22
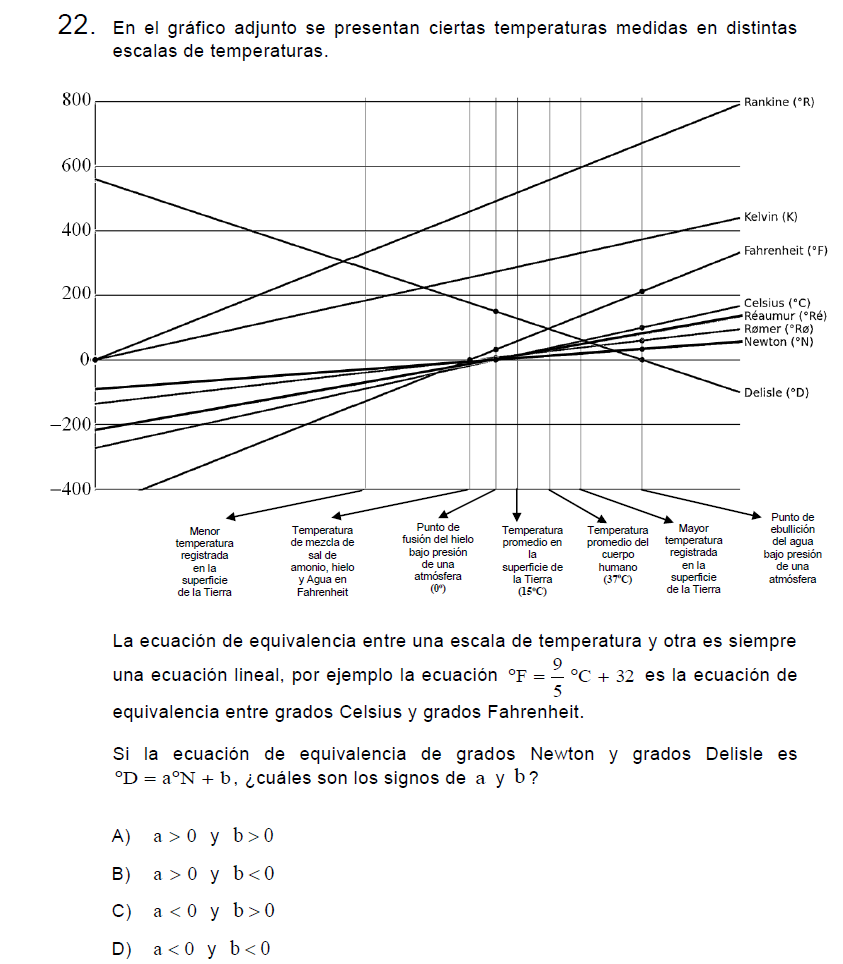
Solución:
La idea para transformar la escala Newton a Delisle radica en convertir su gráfica (la de Newton) en la de Delisle.
La grafica de Newton es creciente y corta al eje Y mucho más abajo que Delisle, quién además es decreciente.
Para poder transformar a Newton deberemos multiplicarla por un coeficiente «a» negativo, de este modo la volvemos decreciente y luego le añadimos un coeficiente «b» positivo, de esta manera cortará al eje Y más arriba, igualando así las condiciones de Delisle.
Letra C.
P23

Solución:
En primer lugar acomodemos un poco la expresión
\[\frac{4x}{5}-\frac{m}{6}<-\frac{1}{10}+\frac{2x}{3}\]
\[\frac{4x}{5}-\frac{2x}{3}<-\frac{1}{10}+\frac{m}{6}\]
\[\frac{12x}{15}-\frac{10x}{15}<-\frac{1}{10}+\frac{m}{6}\]
\[\frac{2x}{15}<-\frac{1}{10}+\frac{m}{6}\]
\[\frac{2x}{15}<-\frac{6}{60}+\frac{10m}{60}\]
\[\frac{2x}{15}<\frac{10m-6}{60}\]
\[4\cdot 2x<10m-6\]
\[8x<10m-6\]
\[x<\frac{10m-6}{8}\]
En esta expresión podemos probar las alternativas y verificar si se cumple el conjunto solución
\[m=-1\to x<-2\]
Letra A.
P24

Solución:
Veamos primero cuanto demora cada computador en realizar el algoritmo una vez
\[A=p\]
\[B=\frac{p}{2}\cdot \frac{1}{3}=\frac{p}{6}\]
Por lo tanto en realizarlo «n» veces se tardarán
\[A=np\]
\[B=\frac{np}{6}\]
Luego nos indican que al realizarlo «n» veces el más rápido, el más rápido (B) demora 60 segundos menos que el otro (A), por lo cual si le sumamos 60 segundos a B podríamos establecer una igualdad.
\[np=\frac{np}{6}+60\]
y de aquí despejamos «p»
\[np-\frac{np}{6}=60\]
\[\frac{6np-np}{6}=60\]
\[\frac{5np}{6}=60\]
\[5np=360\]
\[p=\frac{360}{5n}\]
\[p=\frac{72}{n}\]
Letra A.
P25

Solución:
Vamos traduciendo paso a paso,
La cantidad inicial de gente sería
\[x+y=q\]
la cantidad inicial de dinero recaudado sería
\[mx+ny=p\]
con las modificaciones la cantidad de personas quedaría
\[x+(y-3)=q-3\]
y la cantidad de dinero final será
\[0,70mx+n(y-3)=k\]
esto es
\[x+(y-3)=q-3\]
\[0,70mx+n(y-3)=k\]
Letra A.
P26

Solución:
Podemos factorizar la expresión e igualar trabajando como polinomios
\[px+qx-2p-3q=2x+1\]
\[x(p+q)-2p-3q=2x+1\]
De aquí podemos plantear las siguientes igualdades
\[p+q=2\]
\[-2p-3q=1\]
Y ahora procedemos a resolver el sistema de ecuaciones
Multiplico la primera por 2 y reduzco
\[2p+2q=4\]
\[-2p-3q=1\]
______________________________________
\[-q=5\]
\[q=-5\]
Reemplazo para obtener el valor de p
\[2p+2(-5)=4\]
\[2p-10=4\]
\[2p=14\]
\[p=7\]
Letra B.
P27

Solución:
Que el sistema no tenga solución, significa que ambas rectas son paralelas.
Letra A: todo se ha multiplicado por K de una ecuación a otra, por ende las rectas serán coincidentes.
Letra B: podemos probar rápidamente que no tiene solución igualando ambos miembros izquierdos ya que ambas son iguales a q, quedando
\[kx+ky=x+y\]
\[k(x+y)=x+y\]
\[k=1\]
y luego según el enunciado «k» es distinto de 1, por lo tanto, este sistema no tiene solución.
Letra B.
P28

Solución:
Para que el sistema tenga infinitas soluciones, ambas rectas deben ser coincidentes, esto se logra cuando obtenemos una ecuación a partir de la otra al multiplicarla por algún valor.
A: El primer sistema, con a = 0, nos deja solamente con
\[x+y=1\]
Esta ecuación tiene infinitas soluciones, por ejemplo: 3+(-2)=1, 5+(-4)=1 y así.
Sin embargo, no podemos cumplir la segunda condición ya que si a = 1 (distinto de 0), nos quedan don ecuaciones iguales, es decir, nuevamente infinitas soluciones.
B: Con a = 0, el sistema posee solución única. Pues x = 1.
C: Con a = 0, el tercer sistema se queda solo con la primera ecuación, 2x + y = 1 la cual posee infinitas soluciones.
Para \(a\neq 0\) posee solución única.
D: Para a = 0 no posee solución la primera ecuación.,
Letra C.
P29

Solución:
Comprendamos la situación
\[f(0)=4(f(1)-f(0))\]
\[f(0)=4(500-f(0))\]
\[f(0)=2000-4f(0)\]
\[5f(0)=2000\]
\[f(0)=400\]
Con esto podemos plantear la función modeladora
\[f(x)=100x+400\]
obtengamos \(f(5)\)
\[f(5)=100(5)+400\]
\[f(5)=500+400=900\]
Letra B.
P30

Solución:
Para resolver esta pregunta debemos recordar las propiedades de la suma y multiplicación de las soluciones de una ecuación cuadrática
\[x_1+x_2=\frac{-b}{a}\]
\[x_1\cdot x_2=\frac{c}{a}\]
siendo así
\[m+n=\frac{-1}{5}\]
\[mn=\frac{-5}{5}=-1\]
por lo tanto el ejercicio quedaría
\[(\frac{\frac{-1}{5}}{-1})^{-1}=(\frac{1}{5})^{-1}=5\]
Letra A.
P31

Solución:
Para resolver debemos hacer la diferencia entre
\[8^3x-7^3x=\]
\[512x-343x=\]
\[169x=\]
\[13^2x\]
Letra A.
P32

Solución:
Tenemos un triángulo isósceles donde el lado AC es la base, cuando trazamos la altura que cae a la base de un isósceles, esta divide a la base en partes iguales, por lo tanto, si la base es (x-3), podemos plantear el Teorema de Pitágoras utilizando la mitad de este lado, la altura y la hipotenusa (12), quedando:
\[(\frac{(x-3)}{2})^2+x^2=12^2\]
\[(\frac{(x-3)^2}{4})+x^2=144\]
\[(\frac{(x^2-6x+9)}{4})+x^2=144\]
\[(\frac{(x^2-6x+9)}{4})+\frac{4x^2}{4}=144\]
\[(\frac{(5x^2-6x+9)}{4})=144\]
\[5x^2-6x+9=144\cdot 4\]
\[5x^2-6x+9=576\]
\[5x^2-6x=576-9\]
\[5x^2-6x=567\]
Letra D.
P33

Solución:
Vamos paso a paso:
Si se refleja en torno al eje Y, solamente cambia su coordenada X, quedando su vértice en (1,-1), luego al aplicar el vector traslación quedamos en (1,0), cuya ecuación ya no tiene término libre:
\[(x-1)^2\]
Letra B.
P34

Solución:
Para resolver, debemos reemplazar el valor dado en p(t) y posteriormente despejar t:
\[p(t)=\frac{a}{b}t+b\]
\[\frac{2b}{3}=\frac{a}{b}t+b\]
\[\frac{2b}{3}-b=\frac{a}{b}t\]
\[\frac{2b}{3}-\frac{3b}{3}=\frac{a}{b}t\]
\[-\frac{b}{3}=\frac{a}{b}t\]
\[-\frac{b}{3}\cdot \frac{b}{a}=t\]
\[-\frac{b^2}{3a}=t\]
Letra B.
P35

Solución:
Veamos primero cuánta es la superficie total que debe pintar, para luego determinar la cantidad de galones, es decir, el área del triángulo 3 veces. Ojo que primero debemos transformar la medida a metros.
\[Á=\frac{5\cdot 7}{2}=\frac{35}{2}=17,5\]
Esto x 3
\[3Á=17,5\cdot 3 = 52,5\]
Para esta cantidad es claro que debemos comprar un tarro de galón y otro de medio galón.
Letra D.
P36

Solución:
Vamos viendo una por una
A: Esto no es correcto ya que la figura disminuye en tamaño, las rotaciones no afectan en este sentido, solo «giran» la figura.
B: Esto no es correcto ya que podemos inferir que el centro de homotecia es el origen del plano (A) y que la figura está al otro lado de este centro, por lo tanto, la razón k debe ser negativa.
C: Correcto!
D: De ser esto cierto, al multiplicar las coordenadas de B por k deberíamos obtener P, es decir,
\[k(3,0)=(-2,0)\]
\[\frac{-3}{2}(3,0)=(-2,0)\]
\[(\frac{-9}{2},0)\neq (-2,0)\]
Esto es falso, la razón, es \(\frac{-2}{3}\)
Letra C.
P37

Solución:
Debemos hallar el volumen de este cilindro
\[V=\pi \cdot r^2 \cdot h\]
\[V=\pi \cdot (0,3 cm)^2 \cdot 20 cm\]
\[V=\pi \cdot 0,09 cm^2 \cdot 20 cm\]
\[V=1,8\pi cm^3\]
Letra A.
P38

Solución:
Analicemos las condiciones iniciales:
Si \((a,b)\) está en el segundo cuadrante del plano significa que \(a<0\) y \((b>0)\)
A: Es falso pues podríamos tener el caso \(a=-1, b=6, c=-3\), con esto nos resulta el vector \((-4,3)\) que pertenece al segundo cuadrante.
B: Es falso pues podríamos tener el caso \(a=-1, b=6, c=-3\), con esto nos resulta el vector \(4,-18\) que pertenece al cuarto cuadrante.
C: Es falso pues podríamos tener el caso \(a=-1, b=6, c=-3\), con esto nos resulta el vector \(2,6\) que pertenece al primer cuadrante.
D:Es falso pues podríamos tener el caso \(a=-1, b=6, c=-3\), con esto nos resulta el vector \(-1,18\) que pertenece al segundo cuadrante.
E: Es VERDADERO pues b es positivo y \(0 > a + c\), por lo tanto el vector \((b,a+c)\) pertenece al cuarto cuadrante .
Letra E.
P39

Solución:
Veamos nuevamente paso a paso
\[(-1,7)+(-2,-3)=(-3,4)\]
A este punto le aplicamos la rotación positiva en 90°, es decir, hacemos (-y,x)
\[(-3,4)\to (-4,-3)\]
Letra D.
P40

Solución:
Determinemos en primer lugar, que vector sería necesario aplicar al punto A para obtener el punto B sin tener en cuenta la corriente del río
Deberíamos bajar 4 unidades y retroceder 4, es decir, el vector traslación sería \((-4,-4)\)
La corriente del río impulsa a la nutria solo horizontalmente, por lo tanto, debemos restar el componente «r» asociado a dicha corriente para neutralizarlo, al hacerlo se obtiene el vector
\[(-4-r,-4)\]
Letra C.
P41

Solución:
Obtengamos primeramente el vector w:
\[\vec{w}=(c,d)+(a,b)\]
\[\vec{w}=(c+a,d+b)\]
Para que esté en el primer cuadrante, ambas coordenadas deben ser positivas, es decir,
\[c+a > 0\]
\[d+b > 0\]
De estas relaciones podemos ir despejando las desigualdades para probar las alternativas, por ejemplo
A: Falsa ya que \(c>-a\)
B: Falsa ya que \(a > -c\)
C: Falsa ya que a y b pudieran ser ambos negativos y la multiplicación sería positiva
D: Correcta, ya que esta opción nos indica que todos los valores son positivos y por lo tanto sus sumas también.
E: Falsa ya que todas las coordenadas podrían ser negativas.
Letra D.
P42

Solución:
Para resolver lo importante es identificar la base y la altura de dicho triángulo, una opción para visualizarlo mejor es darle un valor a «P» y reemplazarlo en los puntos. Por ejemplo, con \(p=-1\)
\[A(-1,-2), B(-3,-2), C(-3,-1)\]

El triángulo anterior nos define que la base es claramente el segmento AB y que la Altura es BC
Entonces la altura es la distancia de «p» a «2p», es decir, «p»
Por su parte la base es la distancia de «p» a «p-2», es decir, 2 unidades.
El área será por tanto
\[Á=\frac{2p}{2}=p\to -p\]
Aclaro que el resultado es -p, pues p era un número negativo lo cuál en el contexto geométrico no aplica para medidas.
Letra C.
P43

Solución:
Veamos paso a paso
Paso 1: Error, puesto que Coseno relaciona el cateto adyacente al ángulo y no el opuesto, es decir, debería haber sido
\[cos(60°)=\frac{AO}{OB}\]
Letra A.
P44
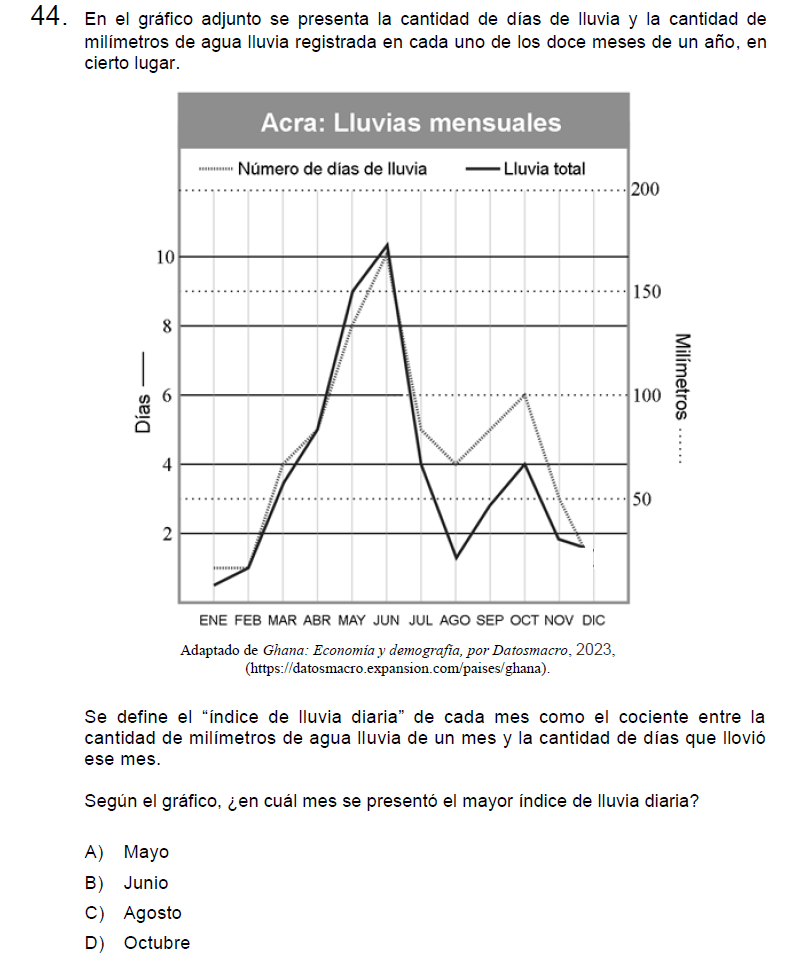
Solución:
Calculemos los índices para cada uno de los meses presentados, como los datos no se logran apreciar del todo, redondearé cada medida hacia arriba.
\[\text{Mayo}=\frac{150}{8}=18,75\]
\[\text{Junio}=\frac{170}{11}=15,45\]
\[\text{Agosto}=\frac{25}{4}=6,25\]
\[\text{Octubre}=\frac{70}{6}=11,7\]
Letra A.
P45

Solución:
Revisemos una a una
A: Falso, la mediana es efectivamente mayor pero en ningún lugar se nos habla acerca de los porcentajes de exigencia de las pruebas.
B: Falso, ya que el rango intercuartil se obtiene al restar el tercer cuartil con el primero.
C: Falso, no conocemos la cantidad de estudiantes que obtuvo el puntaje máximo solo con mirar el gráfico.
D: Correcto!
Letra D.
P46

Solución:
A: Falso. Claramente los promedios de edad son distintos, ya que las edades lo son.
B: Correcto. La variación en las edades para ambas tablas es de 1 año, y se mantiene la misma frecuencia en ambas tablas por lo tanto la desviación estándar es la misma. Sin embargo, como se dijo en A, los promedios son claramente distintos.
Letra B.
P47

Solución:
El promedio de las notas de los estudiantes sería equivalente a sumar todas las notas y dividirlas por la cantidad de estudiantes que rindieron, podemos expresar eso:
Horario 1:
\[\frac{\text{suma 1}}{x+2y}=p\]
Desde donde la suma de todas estás notas sería
\[\text{suma 1}=p(x+2y)\]
Podemos realizar lo mismo para el
Horario 2:
\[\frac{\text{suma 2}}{2x+y}=q\]
Desde donde la suma de todas estás notas sería
\[\text{suma 2}=q(2x+y)\]
Con esto, el promedio final de todos los estudiantes sería equivalente a
\[\frac{Suma 1 + Suma 2}{3x+3y}\]
Si reemplazamos lo obtenido previamente, nos queda
\[\bar{x}=\frac{p(x+2y)+q(2x+y)}{3x+3y}=\frac{p(x+2y)+q(2x+y)}{3(x+y)}\]
Letra A.
P48

Solución:
Para determinar esto necesitamos conocer cuantas cartas de símbolo rojo son también números primos
\[2,3,5,7\]
Estos mismos números se repetirán dos veces (uno para cada símbolo rojo), por lo tanto son 4 de un total de 40 cartas.
\[\frac{8}{40}=\frac{1}{5}\]
Letra A.
P49

Solución:
Que ocurran ambos sucesos simultaneamente siendo independientes nos habla del producto de ambos, es decir,
\[P(A)\cdot P(B) = 0,3\]
\[0,6\cdot P(B) = 0,3\]
\[P(B) = \frac{0,3}{0,6}\]
\[P(B) = 0,5\]
Letra C.
P50

Solución:
Veamos primero cuantos impares tenemos del 1 al 17: 1-3-5-7-9-11-13-15-17, son 9 posibilidades.
La probabilidad será:
\[\frac{9}{17}\cdot \frac{8}{16} \frac{7}{15} \frac{6}{14}\]
\[\frac{3}{17}\cdot \frac{1}{2} \frac{7}{5} \frac{3}{7}\]
\[\frac{3}{17}\cdot \frac{1}{2} \frac{1}{5} \frac{3}{1}\]
\[\frac{9}{170}\]
Letra E.
P51

Solución:
Que gane ambos eventos implica que debemos multiplicar las probabilidades, tenemos una frase como «que gane el primero Y el segundo». Esto sería
\[\frac{2}{30}\cdot \frac{1}{29}=\frac{2}{870}=\frac{1}{435}\]
Letra B.
P52

Solución:
Para que no interseque al eje X, debe cumplirse que su discriminante sea menor que 0, es decir,
\[Δ < 0\]
\[b^2-4ac<0\]
\[9-4ac<0\]
\[9<4ac\]
\[\frac{9}{4}<ac\]
Opción 1: si a = c, nos quedaría
\[\frac{9}{4}<a^2\]
\[\frac{3}{2}<a\]
(estoy ignorando el valor absoluto)
Con esta opción quedamos estancados en este punto, ya que no conocemos el valor de a.
Opción 2: con esta opción conocemos los posibles valores de a, sin embargo, no sabemos nada de c.
Ambas opciones, si combinamos ambas opciones podemos dar respuesta, ya que con 1 sabemos que a debe ser necesariamente mayor que \(\frac{3}{2}\) y la opción 2 lo ratifica.
Letra C.
P53

Solución:
La fórmula planteada para obtener el área de este cuadrilátero corresponde al área de un trapecio, figura que posee dos lados paralelos, p representa la altura en dicha fórmula, sin embargo no tenemos forma de saber si este segmento corresponde o no a dicha altura.
Con la opción 1 sabemos que es un trapecio, sin embargo, nos falta conocer la altura.
Con la opción 2 podemos escribir \(\frac{b_1+b_2}{2}=p\) esta expresión correspondería a la medida de la mediana del trapecio, sin embargo, nos seguiría faltando la medida de la altura.
Con ambas juntas no podemos avanzar mucho más pues sigue faltando la altura.
Letra E.
P54

Solución:
Opción 1: Podemos descartar rápidamente esta opción pensando en el caso de que todos los estudiantes tuvieran un 5,2, en esta situación cumplimos con el promedio dado y ningún estudiante estaría por sobre la nota pedida.
Opción 2: Esta opción si nos permite aseverar que al menos el 50% de los estudiantes está por sobre el 5,2 ya que la definición de mediana nos indica que el 50% de los estudiantes estaría ubicado en el 5,3 o más.
Letra B.
P55

Solución:
Para resolver podemos recurrir a una propiedad de la varianza la cual dice: «Si sumamos a todos los datos de una distribución un mismo número, la nueva varianza se mantiene sin cambios»,
La opción 1, hace alusión a esta propiedad ya que sumamos tres años a todas las personas, por ende su varianza no cambiaría y si ya la conocemos serían iguales.
La opción 2, con estos datos no podemos determinar la varianza, ya que la fórmula para determinarla requiere de conocer cada dato en específico,
\[\sigma ^2=\frac{(x_1-\bar{x})^2+(x_2-\bar{x})^2+…+(x_{n-1}-\bar{x})^2++(x_{n}-\bar{x})^2}{n}\].
Letra A.
