P1

Solución:
Si restamos la cuota fija nos queda un saldo de \(240.000-120.000=120.000\), estos $120.000 podemos dividirlos en 25.000, o bien pensar 25.000 por cuánto nos da cerca de 120.000
\[25.000\cdot 4 =100.000\]
por lo anterior podemos afirmar que es posible arrendar el juego por un máximo de 8 horas (con una más nos pasamos del presupuesto)
Letra B.
P2

Solución:
Para resolver debemos recordar que podemos calcular porcentajes multiplicando el número inicial por un decimal, por ejemplo, si multiplicamos 20 por 1,35 estamos aumentando a 20 en un 35% o si multiplicamos a 20 por 0,6 estamos disminuyendo a 20 en un 40%.
Si multiplicamos a p por 1,25 le aumentamos en un 25% y si la multiplicamos por 0,75 la disminuimos en un 25%.
Letra A.
P3
Solución:
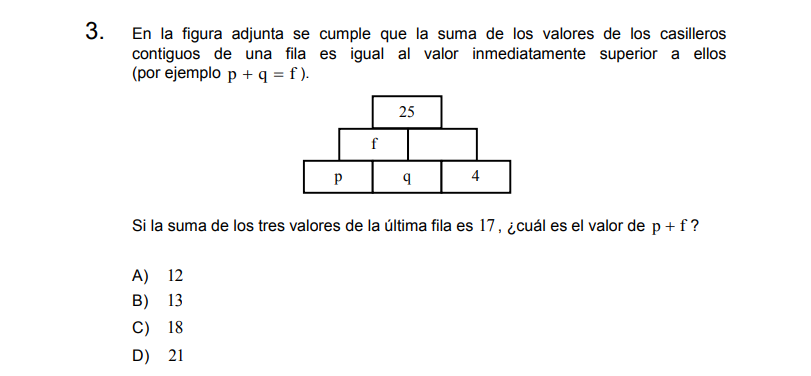
Si la última fila suma 17 significa que \(p+q+4=17\), por lo tanto
\[p+q=13\]
de lo anterior se desprende que \(f=13\), el espacio en blanco al lado de \(f\) debe ser 12 (junto a f suman 25). Esto implica que \(q+4=12\) y por lo tanto
\[q=8\]
de lo anterior tenemos que
\[p+8=13\]
\[p=5\]
finalmente
\[p+f=\]
\[5+13=18\]
Letra C.
P4

Solución:
Esta pregunta puede ser resuelta utilizando el «principio multiplicativo» (puedes revisarlo en mi página), este principio, en palabras sencillas, nos permite determinar la cantidad de posibilidades que tenemos de escoger algo por medio de multiplicar las opciones que se nos dan.
Para la primera automotora «Mi auto» sería:
\[5\cdot 3 \cdot 3 = 45\]
Para la segunda automotora «Viaje Feliz» sería:
\[4\cdot 3 \cdot 4 = 48\]
Letra A.
P5

Solución:
Para resolver podemos probar las alternativas o bien plantear ecuaciones, haré lo segundo
\[(\frac{160+x_1}{2},\frac{60+x_2}{2},\frac{120+x_3}{2})=(170,80,60)\]
- \(\frac{160+x_1}{2}=170\)
\[160+x_1=340\]
\[x_1=180\]
- \(\frac{60+x_2}{2}=80\)
\[60+x_2=160\]
\[x_2=100\]
- \(\frac{120+x_3}{2}=60\)
\[120+x_3=120\]
\[x_3=0\]
Letra C.
P6

Solución:
Podemos dar un ejemplo para clarificar la situación,
Si en Chile es la 01:00 en Nueva Zelanda son las 17:00 mientras que en México son las 00:00, con este ejemplo se ve claramente que desde México a Nueva Zelanda debemos sumar 17 hrs.
Letra D.
P7

Solución:
Para resolver este problema podemos pensar en la ganancia que obtiene por kilogramo vendido, si compró 3 kilogramos en $600 significa que compra a $200 cada kilogramo. Si vende 4 en $1000, significa que vende a $250 cada kilogramo, por lo tanto, recibe $50 de ganancia por cada kilogramo vendido.
Con esto claro para saber cuantos kilogramos debe vender para obtener una ganancia de $3000 basta con dividir 3000 en 50 lo que da 60.
Letra D.
P8
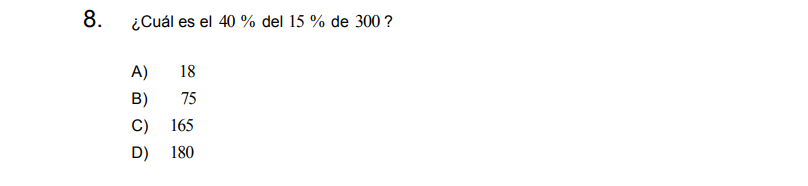
Solución:
Para resolver escribo los porcentajes sucesivos como multiplicaciones
\[\frac{40}{100} \cdot \frac{15}{100} \cdot 300=\]
\[\frac{4}{10} \cdot \frac{15}{1} \cdot 3=\]
\[\frac{4}{2} \cdot \frac{3}{1} \cdot 3=\]
\[2 \cdot 3 \cdot 3=\]
\[18\]
Letra A.
P9

Solución:
La equivalencia en decimales de 120% es 1,20. Solo falta traducir lo solicitado, el valor del helado aumentado en su 120%, significa que al valor original debemos sumarle el 120% del precio por lo tanto nos queda
\[500+1,20\cdot 500=\]
\[500(1+1,20)=\]
\[500\cdot (2,20)\]
Letra D.
P10

Solución:
El 25% de algo siempre es equivalente a un cuarto de ese algo, o bien dividir ese algo en 4, si tenemos inicialmente 8 su 25% equivale a 2 (8:4), por lo que al añadirle este 25% quedaría con 10 puntos (10 cuadrados).
Letra C.
P11

Solución:
Debemos probarlas todas considerando el total de 25 personas.
A. 80% de 25 es \(\frac{80}{100}\cdot 25\)
\[\frac{8}{10}\cdot 25=\]
\[\frac{8}{2}\cdot 5=\]
\[4\cdot 5=20\]
Almibar + Quitased = 12 + 8 = 20
Afortunadamente dimos con la respuesta correcta inmediatamente.
Letra A.
P12

Solución:
Trabajemos con una proporción
\[\frac{\text{%}}{cantidad}=\frac{x}{4740}=\frac{100}{15800}\]
\[\frac{x}{4740}=\frac{100}{15800}\]
\[x=\frac{100\cdot4740}{15800}\]
\[x=\frac{1\cdot4740}{158}\]
\[x=\frac{4740}{158}\]
\[x=\frac{2370}{79}\]
\[x=30\]
Letra D.
P13

Solución:
Probaremos lo que dice cada uno
Sebastián: Primero necesitamos la cantidad de personas que omitieron (25+35=60), por lo tanto, 60 de 200 han omitido, lo cual corresponde a un 30% del total.
Angélica: A primera lectura parece correcto, sin embargo, el punto de partida es diferente, es decir, se está considerando 10% del total de omisión de la primera encuesta y no del total de votantes de la primera encuesta.
Luisa: Está en lo correcto!
Manuel: No podemos deducir esto ya que no conocemos los datos de las preguntas.
Letra C.
P14
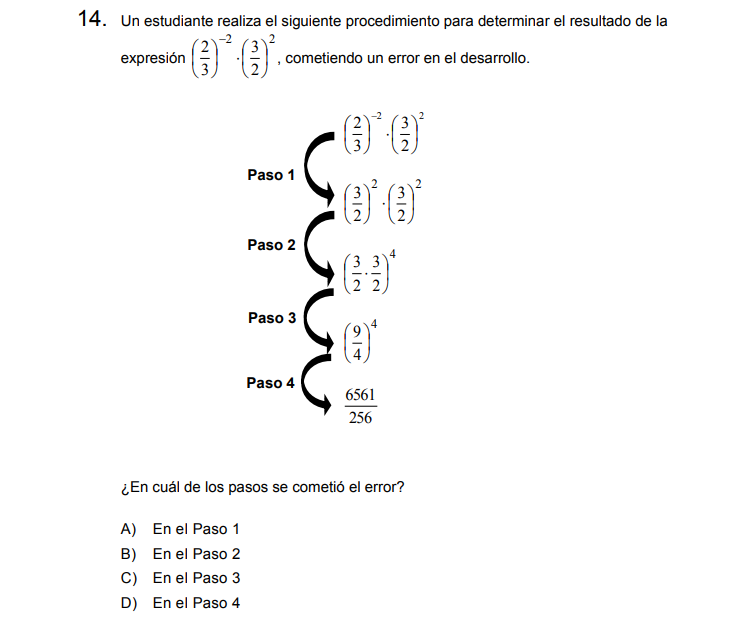
Solución:
El error se encuentra en el paso 2, al multiplicar potencias de igual base, conservamos la base (1 sola de ellas) y sumamos los exponentes \((\frac{3}{2})^4\).
Letra B.
P15
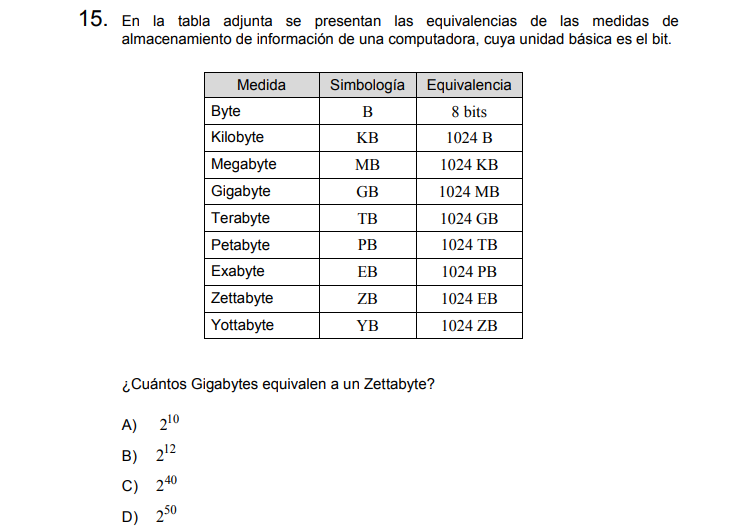
Solución:
Para resolver iré retrocediendo
\[1ZB=1024EB\]
\[1ZB=1024\cdot1024PB\]
\[1ZB=1024\cdot1024\cdot1024TB\]
\[1ZB=1024\cdot1024\cdot1024\cdot1024GB\]
Ahora convertiré todo en potencias de base 2
\[1ZB=2^{10}\cdot2^{10}\cdot2^{10}\cdot2^{10}GB\]
\[1ZB=2^{40}GB\]
Letra C.
P16
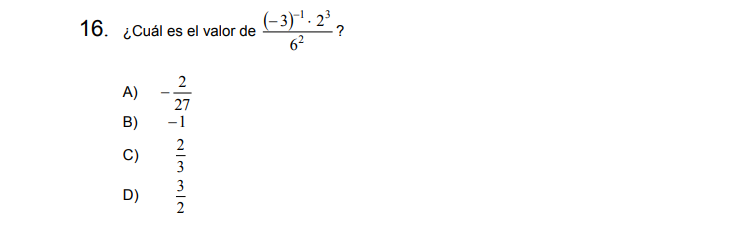
Solución:
Vamos paso a paso
\[\frac{(-3)^{-1}\cdot2^3}{6^2}=\]
El exponente negativo de -3 nos lleva a invertir la base
\[\frac{-\frac{1}{3}\cdot2^3}{6^2}=\]
Podríamos seguir aplicando propiedades pero creo que es más rápido calcular y resolver
\[\frac{-\frac{1}{3}\cdot8}{36}=\]
\[\frac{-\frac{8}{3}}{36}=\]
\[-\frac{8}{3}\cdot\frac{1}{36}=\]
\[-\frac{2}{3}\cdot\frac{1}{9}=\]
\[-\frac{2}{27}\]
Letra A.
P17
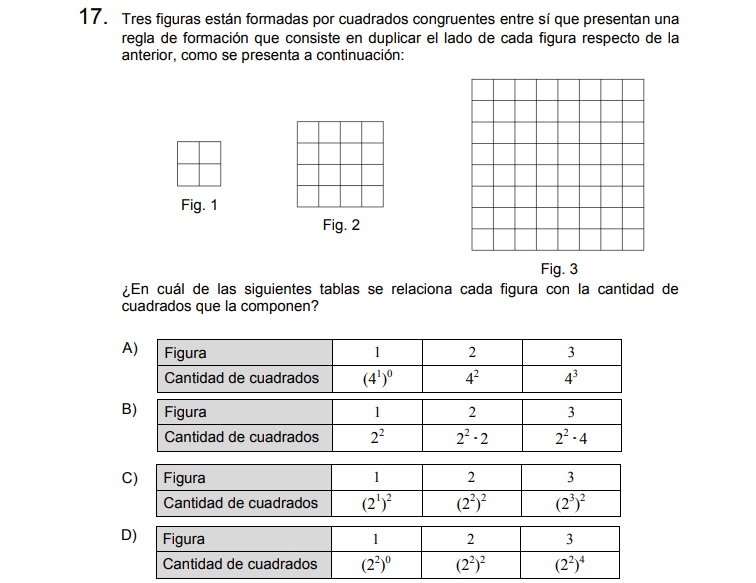
Solución:
Probemos en orden
A. en la figura 1 dice que hay \((4^1)^0\) cuadros, esto es erróneo ya que eso significaría que hay 1 solo cuadrado (la potencia 4 elevado a 0 da 1).
B. Basta probar con la figura 2, pues dice que tiene 8 cuadrados. Falso!
C. La cantidad de cuadrados respectivamente por figura sería 4, 16, 64. Correcto!
D. Falla nuevamente en la cantidad de la primera figura.
Letra C.
P18
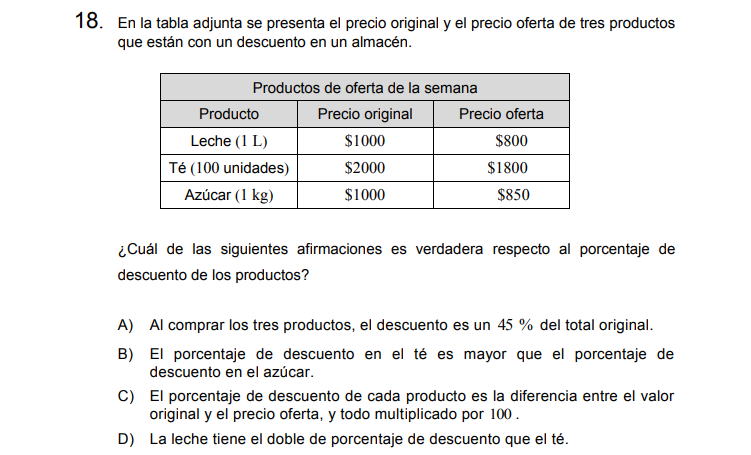
Solución:
Nos toca probar las alternativas, iremos 1 a 1
A. Compra total original: 4000, Compra total precio oferta: 3450.
Con una proporción entre estos precios podemos obtener el porcentaje \(\frac{\text{%}}{cantidad}=\frac{100}{4000}=\frac{x}{3450}\)
\[\frac{100}{4000}=\frac{x}{3450}\]
\[\frac{100\cdot3450}{4000}=x\]
\[\frac{1\cdot345}{4}=x\]
\[86,25=x\]
Por lo tanto el descuento es menor del 20%
B. El 10% de 2000 es 200, por lo tanto el descuento en el té es de un 10%. Por otro lado 150 es un 15% de 1000 por lo tanto el descuento en el azúcar es de un 15%, se descuenta más en el azúcar que en el té.
C. Esto implicaría que el descuento del té es 200 x 100, incorrecto!
D. El % de descuento de la leche es de un 20% ya que 200 es un 20% de 1000. El té solo tenía un 10% de descuento, ósea la mitad.
Letra D.
P19

Solución:
Este tipo de problemas se resuelve con una expresión exponencial (el periodo (n) en el exponente), la expresión base es
\[\text{cantidad inicial} \cdot \text{tasa de cambio}^{\text{periodo}} \]
\[320\cdot4^n\]
Letra B.
P20

Solución:
El área de un rectángulo se calcula multiplicando largo por ancho, por lo tanto
- \(\text{ancho}=3^k\)
- \(\text{largo}=3\cdot3^k\)
Área \(=3^k\cdot 3\cdot 3^k\)
\[Área =3\cdot3^{k+k}\]
\[Área =3\cdot3^{2k}\]
\[Área =3^{2k+1}\]
Letra C.
P21
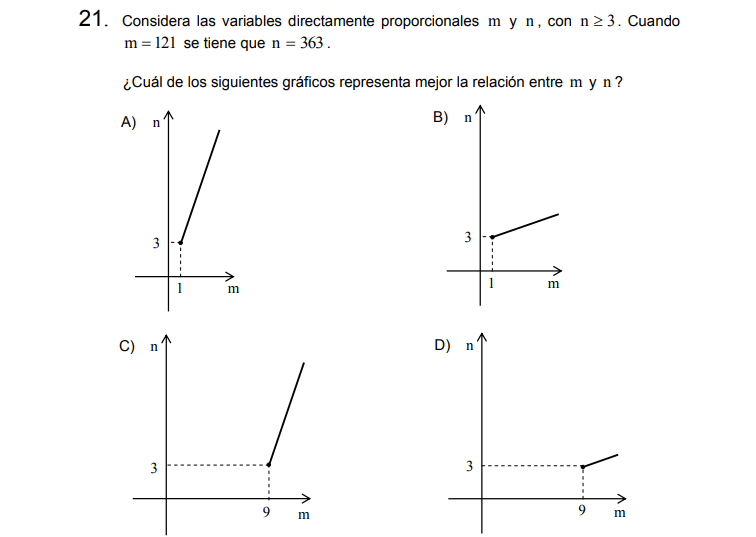
Solución:
Planteemos la razón para entender mejor la situación, tenemos que \(m:n\) como \(121:363\) lo que es equivalente a \(1:3\), esto traducido significa que por cada unidad que nos movamos en \(m\) nos moveremos 3 unidades en \(n\), esto está representado de mejor manera en el gráfico A, quién pudiera causar confusión es el gráfico B, sin embargo, su inclinación es «muy suave». Otra forma de resolver es que den dos puntos (1,3) y (2,6) por ejemplo y tracen la recta que pasa por esos puntos.
Letra A.
P22

Solución:
Para resolver podemos hacer uso de la propiedad asociativa y dejar la expresión de una manera más conveniente \((a+(b+c))\cdot(a+(b-c))=\)
\[((a+b)+c))\cdot((a+b)-c))=\]
esta expresión se pude resolver como una «suma por su diferencia«
\[((a+b)+c))\cdot((a+b)-c))=(a+b)^2-(c)^2\]
\[(a+b)^2-(c)^2=\]
\[a^2+2ab+b^2-c^2\]
Letra B.
P23
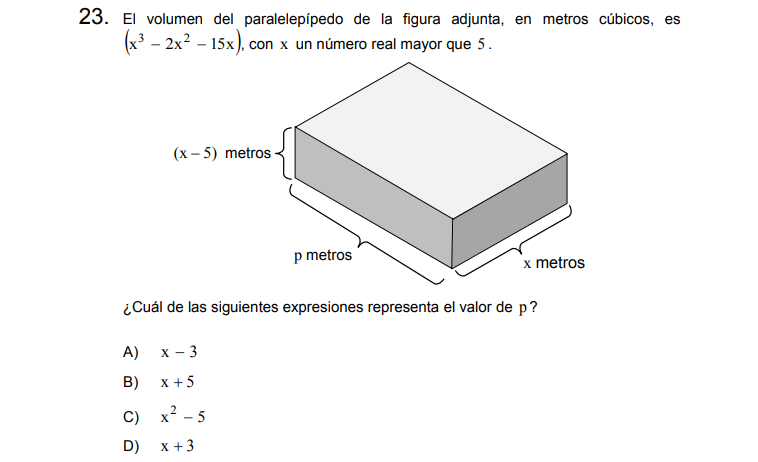
Solución:
Para resolver les recomiendo factorizar la expresión del volumen, quizá determinemos inmediatamente el valor de p.
\[x^3-2x^2-15x=\]
\[x(x^2-2x-15)=\]
\[x(x-5)(x+3)\]
El término faltante es \(x+3\)
Letra D.
P24

Solución:
Procedamos a factorizar
\[(a+1)^2+(a+1)(a-3)=\]
\[(a+1)[(a+1)+(a-3)]=\]
\[(a+1)[a+1+a-3]=\]
\[(a+1)[2a-2]\]
Letra D.
P25

Solución:
Para resolver debemos observar ingrediente por ingrediente, el azúcar le alcanza para repetir la receta 5 veces, la mantequilla para 4, la harina para 3 y los huevos para 4 veces, por lo tanto, nos quedamos con el número menor, es decir, la harina, podrá realizar tres veces la receta esto es \(3\cdot 12 = 36\) galletas.
Letra A.
P26
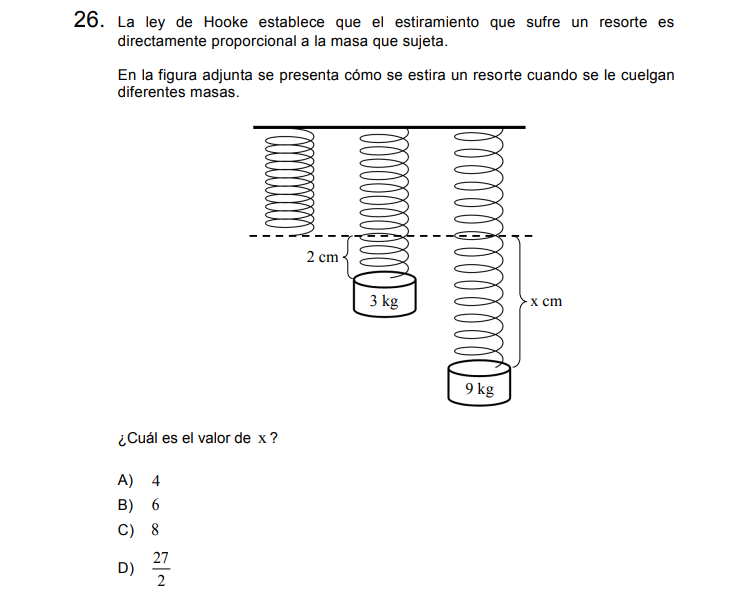
Solución:
Como se nos dice que la ley establece una relación directamente proporcional, podemos plantear una proporción para determinar \(x\)
\[\frac{\text{longitud}}{\text{masa}}=\frac{2}{3}=\frac{x}{9}\]
\[\frac{2}{3}=\frac{x}{9}\]
\[\frac{2\cdot 9}{3}=x\]
\[\frac{2\cdot 9}{3}=x\]
\[2\cdot 3=x\]
\[6=x\]
Letra B.
P27

Solución:
Para resolver plantearemos una proporción pues se nos indica que de ancho deben ser dos cabezas
\[\frac{\text{cm}}{\text{cabezas}}=\frac{15}{7\frac{1}{2}}=\frac{x}{2}\]
\[\frac{15}{7\frac{1}{2}}=\frac{x}{2}\]
\[\frac{15\cdot 2}{7\frac{1}{2}}=x\]
\[\frac{15\cdot 2}{7,5}=x\]
\[2\cdot 2=x\]
\[4=x\]
Letra C.
P28

Solución:
A. Si excede en 10 hubiera ido a 40 \(\frac{km}{h}\)
B. Falso, solo puede llegar a 100 \(\frac{km}{h}\)
C. Falso iba a 30 \(\frac{km}{h}\)
D. Correcto!
Letra D.
P29

Solución:
Resolveremos planteando una inecuación
\[100x+5000\leq 50000\]
\[100x\leq 45000\]
\[x\leq 450\]
Letra A.
P30
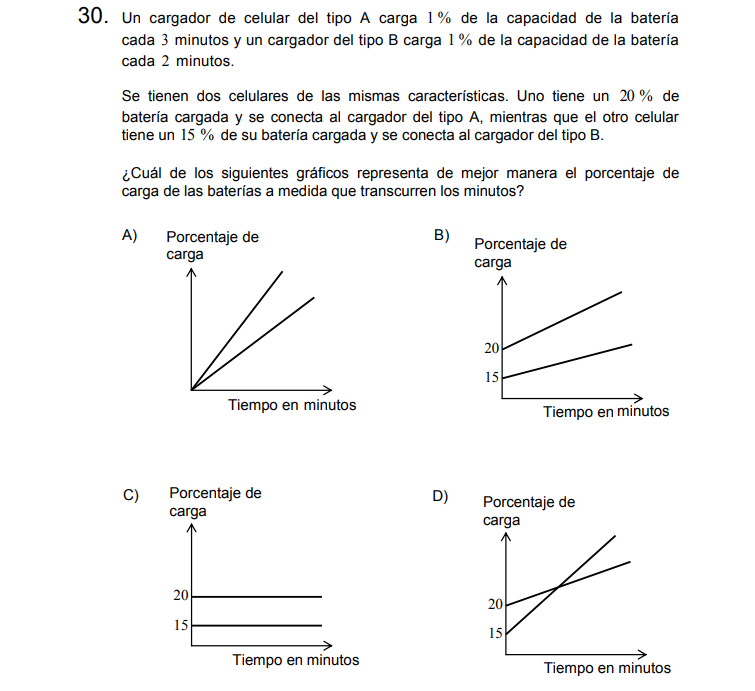
Solución:
La respuesta correcta es D, ya que:
Se muestra el punto de inicio de la batería al momento de ser conectado.
La pendiente del tipo B (15%) tiene una pendiente más pronunciada que la del tipo A, ya que requiere menos tiempo para subir un 1% de batería.
Letra D.
P31

Solución:
Precio durazno \(=480\)
Precio mango \(= 400\)
Cantidad de mangos \(+\) Cantidad de duraznos \(=16\)
Definimos que \(\text{durazno}=x\) por lo tanto tenemos que
\[x+\text{Cantidad mangos}=16\]
\[\text{Cantidad mangos}=16-x\]
Ahora con las cantidades definidas, multiplicamos por los respectivos precios e igualamos al total gastado.
\[480\cdot x +(16-x)\cdot 400 = 6800 \]
Letra A.
P32
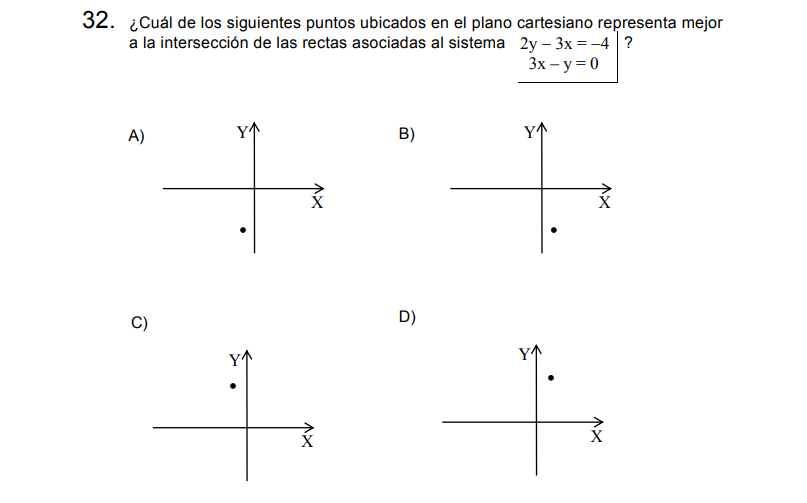
Solución:
Determinar la intersección de ambas rectas (ambas ecuaciones) significa resolver el Sistema de Ecuaciones, ustedes pueden utilizar el método que más les guste, yo acomodaré las ecuaciones y utilizaré reducción
\[-3x+2y=-4\]
\[3x-y=0\]
Sumamos hacia abajo ambas ecuaciones quedando
\[y=-4\]
Con esto podemos encontrar el valor de \(x\), reemplazando el valor encontrado en cualquiera de las dos ecuaciones
\[3x-y=0\]
\[3x-(-4)=0\]
\[3x+4=0\]
\[3x=-4\]
\[x=\frac{-4}{3}\]
El punto de intersección es
\[(\frac{-4}{3},-4)\]
Letra A.
P33

Solución:
Resolvemos la ecuación cuadrática, en este caso lo haré factorizando
\[x^2-12x+35=0\]
\[(x-7)(x-5)=0\]
\[x-7=0 \text{ } \text{ o } \text{ } x-5=0\]
\[x_1=7\]
\[x_2=5\]
Letra C.
P34
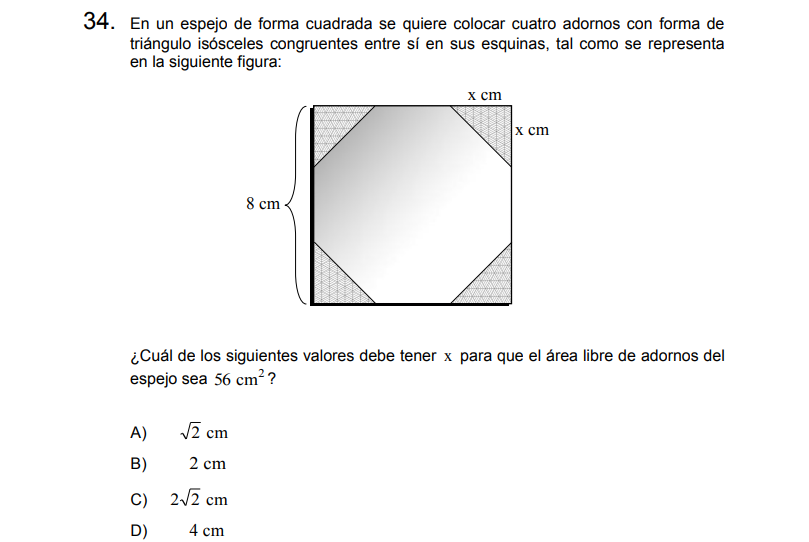
Solución:
Para resolver calcularemos primero el área total (el cuadrado) y le restaremos las áreas de los 4 triángulos
\[Á_{\text{cuadrado}}=8^2=64\]
\[Á_{\text{triángulos}}=4\cdot \frac{x\cdot x}{2}=4\cdot \frac{x^2}{2}=2x^2\]
Restamos ambas e igualamos a 56
\[64-2x^2=56\]
\[64-56=2x^2\]
\[8=2x^2\]
\[4=x^2\]
\[x_1=2, x_2=-2\]
Nos quedamos con el valor positivo
Letra B.
P35

Solución:
En primer lugar, el punto de inicio del «segmento» debe ser tocando al eje Y en 80, ya que horizontalmente se ha representado el tiempo y es en ese lugar donde el tiempo inicial es 0 segundos.
En segundo lugar calcularemos cuanto tiempo tardará en llegar al suelo
\[80:5=16\]
Por lo tanto, a los 16 segundos ha llegado al suelo
Letra C.
P36

Solución:
Vamos una a una
A. El costo fijo es de 2.500
B. Correcta ya que multiplica por el factor 1.5.
C. El costo fijo es de 2.500
D. El recargo es del 50%
Letra B.
P37

Solución:
Para resolver plantearemos un sistema
Sea «x» la cantidad de bidones de 3L y sea «y» la cantidad de bidones de 5L
\[x+y=100\]
\[3x+5y=360\]
utilizando el método de reducción (multiplicando la primera ecuación por -3) quedaría
\[-3x+-3y=-300\] \[3x+5y=360\]
sumando ambas ecuaciones
\[2y=60\] \[y=30\]
con este valor sacamos x
\[x+y=100\]
\[x+30=100\]
\[x=70\]
Finalmente realizamos la diferencia entre las cantidades
\[x-y=\]
\[70-30=40\]
Letra B.
P38
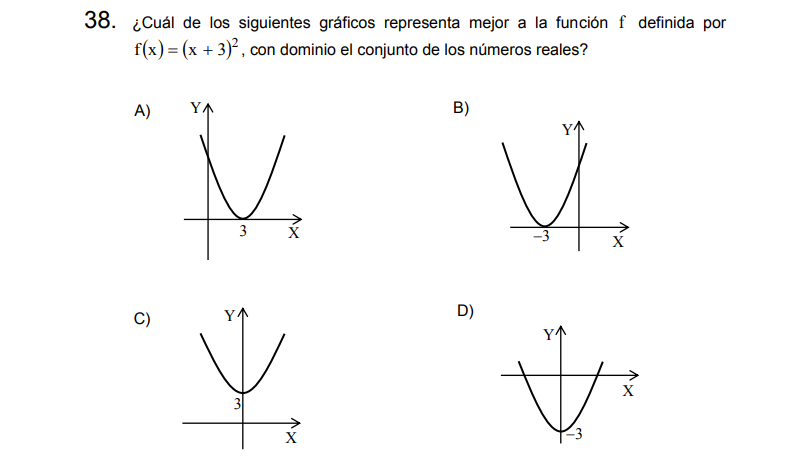
Solución:
Esta pregunta puede ser fácilmente resuelta recordando los «desplazamientos» en funciones, en este caso si añadimos una cantidad en el paréntesis de la función el desplazamiento será lateral y contrario al signo de lo que se añade, para este caso particular sería desplazar el vértice de la función (0,0) tres unidades a la izquierda quedando situada en (-3,0)
Si no recuerdan los desplazamientos deberán desarrollar la expresión y encontrar el vértice utilizando la fórmula. :D.
Letra B.
P39
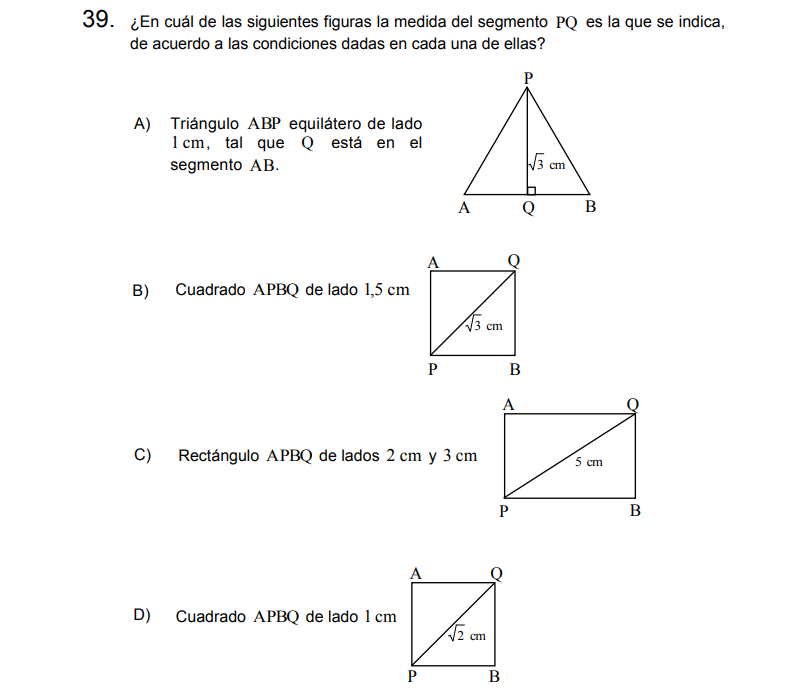
Solución:
A. Se puede demostrar que «La altura \((h)\) de un triángulo equilátero es igual a la mitad de la medida de su lado (\(a\)) multiplicada por \(\sqrt{3}\)», es decir:
\[h=\frac{a}{2}\cdot \sqrt{3}\]
En nuestro caso, si la medida del lado es 1, su altura debiera ser \(\frac{1}{2}\cdot \sqrt{3}\).
B. Se puede demostrar que «La diagonal \((d)\) de un cuadrado es igual a la medida de su lado \((a)\) multiplicada por \(\sqrt{2}\)», es decir:
\[d=a\sqrt{2}\]
En nuestro caso, si la medida del lado es \(\frac{3}{2}\), su diagonal debiera ser \(\frac{3}{2}\cdot \sqrt{2}\).
C. Si se tiene un rectángulo con medidas 2 y 3, podemos obtener su diagonal utilizando el Teorema Pitágoras:
\[d=\sqrt{2^2+3^2}\]
\[d=\sqrt{4+9}\]
\[d=\sqrt{13}\]
D. Como ya mencione la diagonal del cuadrado es el lado multiplicado por \(\sqrt{2}\), por lo tanto si su lado mide 1, su diagonal será \(d=1\cdot \sqrt{2}=\sqrt{2}\)
Letra D.
P40

Solución:
En primer lugar obtenemos la medida del cateto en contacto con la repisa (horizontal, el de arriba :D), esto es \(\frac{2}{3} \text{de 30 cm}\)
\[\frac{2}{3}\cdot 30 = 20\]
Ahora planteamos el T. de Pitágoras incluyendo la segunda condición (la referida a la hipotenusa), donde «x», será la medida del cateto que va en la pared.
\[(20)^2+x^2=(40)^2\]
\[400+x^2=1600\]
\[x^2=1200\]
\[x=\sqrt{1200}\]
\[x=\sqrt{400\cdot3}\]
\[x=20\sqrt{3}\]
Letra C.
P41
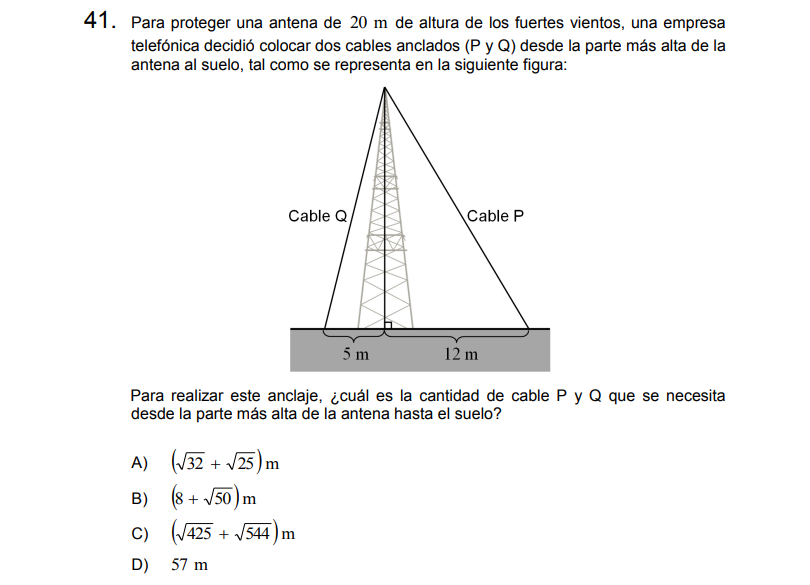
Solución:
Para resolver utilizamos el T. de Pitágoras con ambos triángulos, sabiendo que el cateto (vertical) mide 20m
\[5^2+20^2=Q^2\]
\[25+400=Q^2\]
\[425=Q^2\]
\[\sqrt{425}=Q\]
Ahora la otra
\[12^2+20^2=P^2\]
\[144+400=P^2\]
\[544=P^2\]
\[\sqrt{544}=P\]
Para la cantidad total, sumamos ambas medidas
\[P+Q=\]
\[\sqrt{425}+\sqrt{544}\]
Letra C.
P42
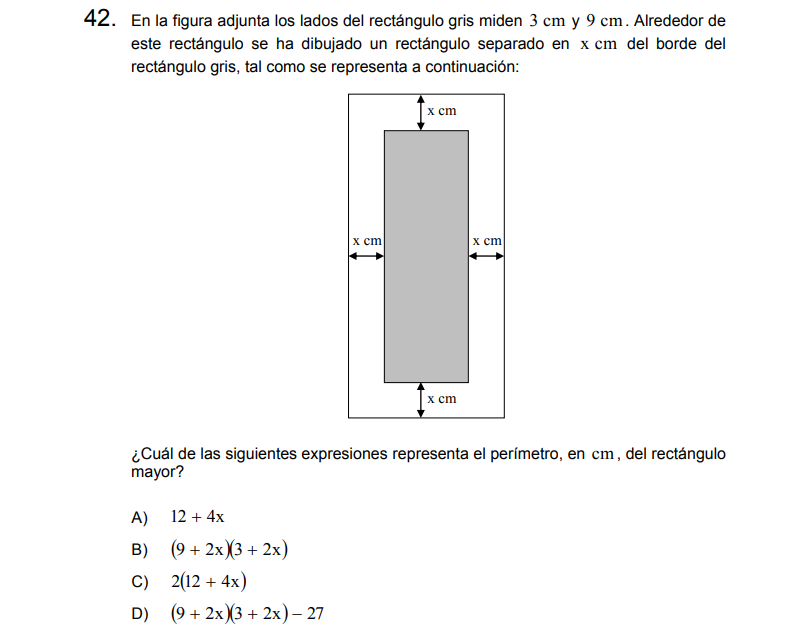
Solución:
Si el ancho del rectángulo gris es 3 el ancho del rectángulo mayor será
\[3+x+x=2x+3\]
Si el largo del rectángulo gris es 9 el largo del rectángulo mayor será
\[9+x+x=2x+9\]
Con estos datos el perímetro del rectángulo mayor será:
\[2\cdot\text{ancho}+2\cdot{largo}=\]
\[2\cdot (2x+3)+2\cdot(2x+9)=\]
\[4x+6 + 4x+18=\]
\[8x+24\]
lo cual es equivalente a
\[2(4x+12)\]
Letra C.
P43

Solución:
Recordemos en primer lugar que el volumen de un cilindro recto se calcula como
\[V=\pi\cdot r^2\cdot h\]
En este caso sería
\[V=\pi \cdot r^2 \cdot 20 = 20r^2\cdot \pi\]
Si se aumenta el volumen en un 20% equivaldría a multiplicar toda la expresión por 1,2 quedando
\[V_f=V\cdot 1,2\]
\[V_f=20r^2\cdot \pi \cdot 1,2 \]
\[V_f=24\cdot r^2\cdot \pi\]
Letra B.
P44

Solución:
Para resolver este problema debemos ir por partes, en primer lugar vamos a determinar la cantidad de agua que debe beber esta persona, para ello plantearemos una proporción, sin embargo, nos quedarán datos expresados con letras, además cambiamos el 1 Litro por 1000 haciendo alusión a los \(cm^3\)
\[\frac{Agua}{Peso}=\frac{1000}{35}=\frac{x}{P}\]
\[\frac{1000}{35}=\frac{x}{P}\]
\[\frac{1000\cdot P}{35}=x\]
La cantidad de agua que debe beber esta persona es \(\frac{P}{35}\cdot 1000\)
Ahora debemos determinar cuantas veces debe beberse la botella, para ello dividimos la cantidad de agua que debe beber por la capacidad (volumen) de la botella, es decir:
\[\frac{P\cdot 1000}{35}:V=\]
\[\frac{P\cdot 1000}{35}:\pi \cdot r^2 \cdot h=\]
\[\frac{P\cdot 1000}{35}\cdot \frac{1}{\pi \cdot r^2 \cdot h}=\]
\[\frac{P\cdot 1000}{35\pi \cdot (3)^2 \cdot 20}=\]
\[\frac{P\cdot 1000}{35\pi \cdot 9 \cdot 20}=\]
\[\frac{\frac{P}{35}\cdot 1000}{\pi \cdot 9 \cdot 20}\]
Letra C.
P45
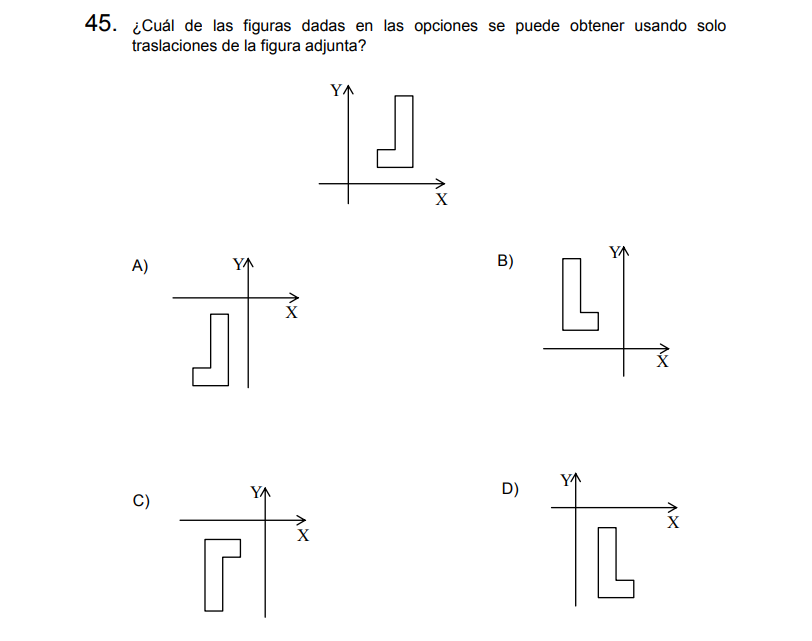
Solución:
Al efectuar traslaciones la figura mantiene su orientación, solo se desplaza, por lo tanto, cualquier figura que apunte en otra dirección queda descartada, siendo así, B, C y D quedan descartadas!
Letra A.
P46

Solución:
Para resolver anotaremos los movimientos a realizar y luego los sumaremos para determinar el vector que nos solicitan
1. (3,2)
2. (-4,-5)
Si los sumamos
\[(3,2)+(-4,-5)=\]
\[(3+(-4),(2+-5))=\]
\[(-1,-3)\]
Letra B.
P47

Solución:
El eje de simetría en palabras sencillas nos indica una recta por la cual si nosotros doblamos la figura calza de manera perfecta, es como colocar un espejo que refleja el otro lado de manera perfecta.
En este caso la única que tiene más de dos ejes de simetría es la rueda.
Letra C.
P48

Solución:
Para encontrar el punto P debemos ir retrocediendo,
Al punto R lo trasladaremos según el vector \((2,-3)\) así obtendremos el punto Q
\[(5,4)+(2,-3)=(7,1)\]
Reflejar este punto respecto al origen significa cambiar ambos signos del punto, nos resultaría el punto
\[(-7,-1)\]
Letra B.
P49
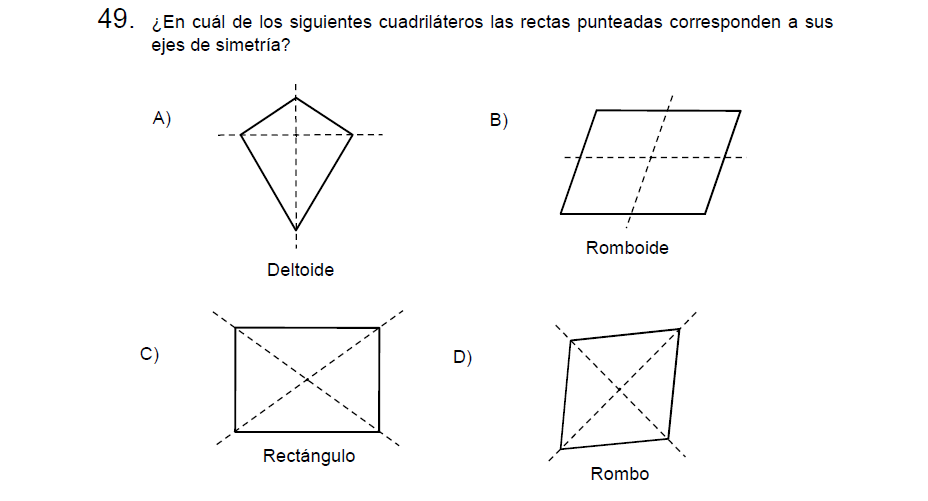
Solución:
Comentamos anteriormente que el eje de simetría puede verse como el pliegue perfecto, en este caso el único que lo cumple es el Rombo.
Letra D.
P50
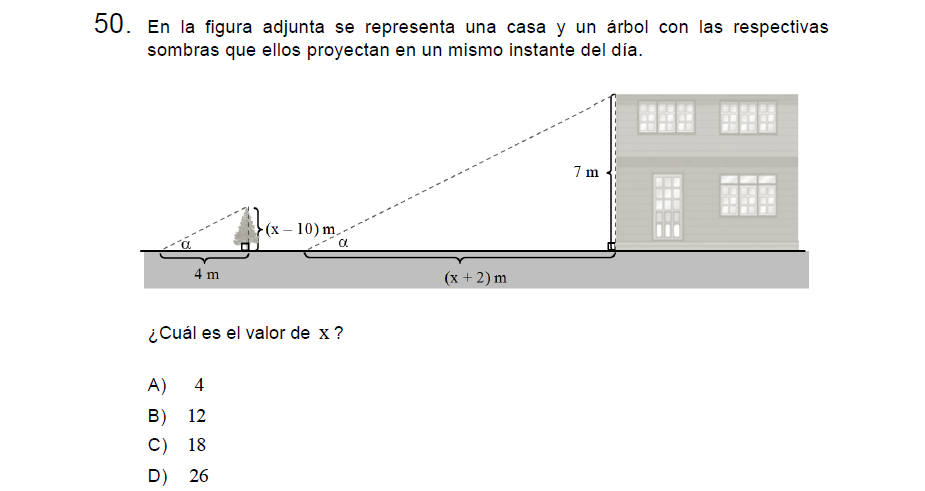
Solución:
Para resolver utilizaremos semejanza de triángulos, podemos plantear la relación sombra es a alto:
\[\frac{Sombra}{alto}=\frac{4}{x-10}=\frac{x+2}{7}\]
Ahora resolvemos
\[\frac{4}{x-10}=\frac{x+2}{7}\]
\[4\cdot 7=(x+2)(x-10)\]
\[28= x^2 -8x -20\]
Resolvemos esta ecuación cuadrática y obtenemos la respuesta
\[0=x^2-8x-48\]
\[0=(x+4)(x-12)\]
\[x_1=12\]
\[x_2=-4\]
Nos quedamos con el valor positivo ya que estamos en un contexto realista.
Letra B.
P51
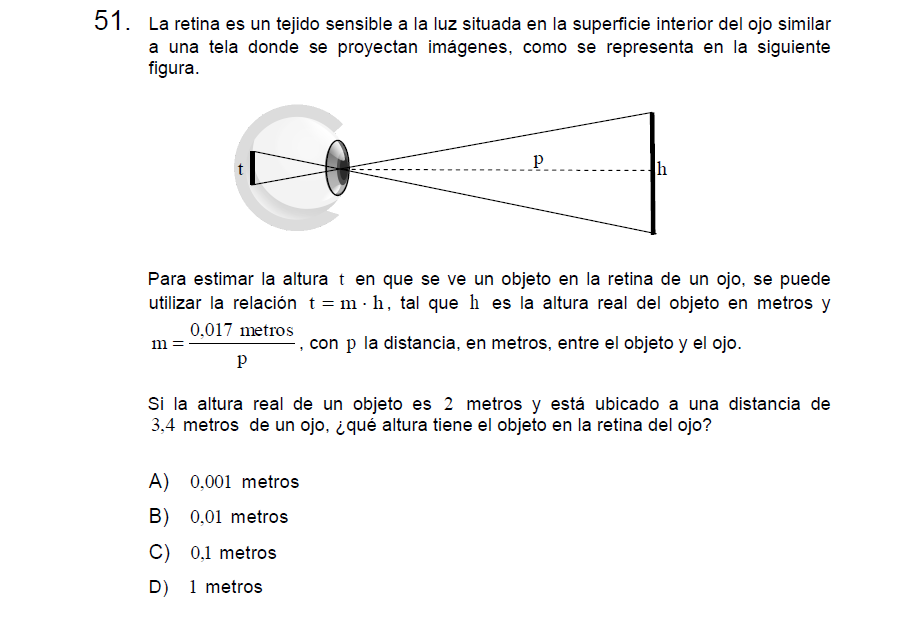
Solución:
Debemos reemplazar los datos dados en la fórmula
\[t=m\cdot h\]
\[t=\frac{0,017}{3.4}\cdot 2\]
\[t=\frac{0,034}{3.4}\]
\[t=\frac{3.4 \cdot 10 ^{-2}}{3.4}\]
\[t=1\cdot 10^{-2}\]
\[t=0.01\]
Si no recuerdan notación científica, vayan a ver mi post de potencias :D.
Letra B.
P52
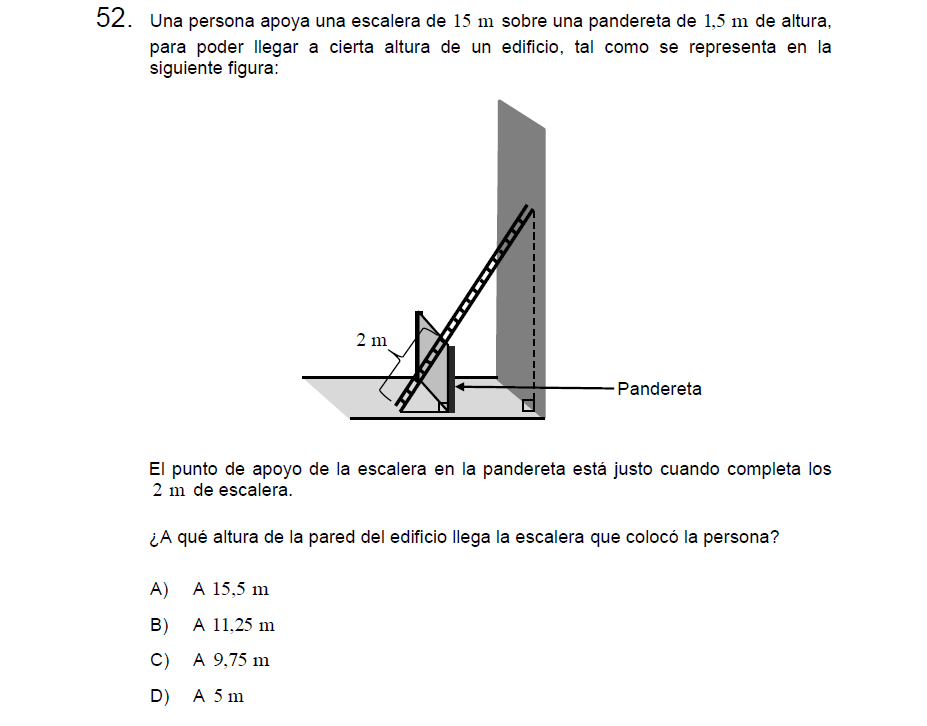
Solución:
Resolveremos utilizando semejanza de triángulos planteando una proporción
\[\frac{Diagonal}{alto}=\frac{2}{1.5}=\frac{15}{x}\]
Con esto podemos obtener el alto
\[\frac{2}{1.5}=\frac{15}{x}\]
\[2x=15\cdot 1.5\]
\[2x=22.5\]
\[x=11.25\]
Letra B.
P53
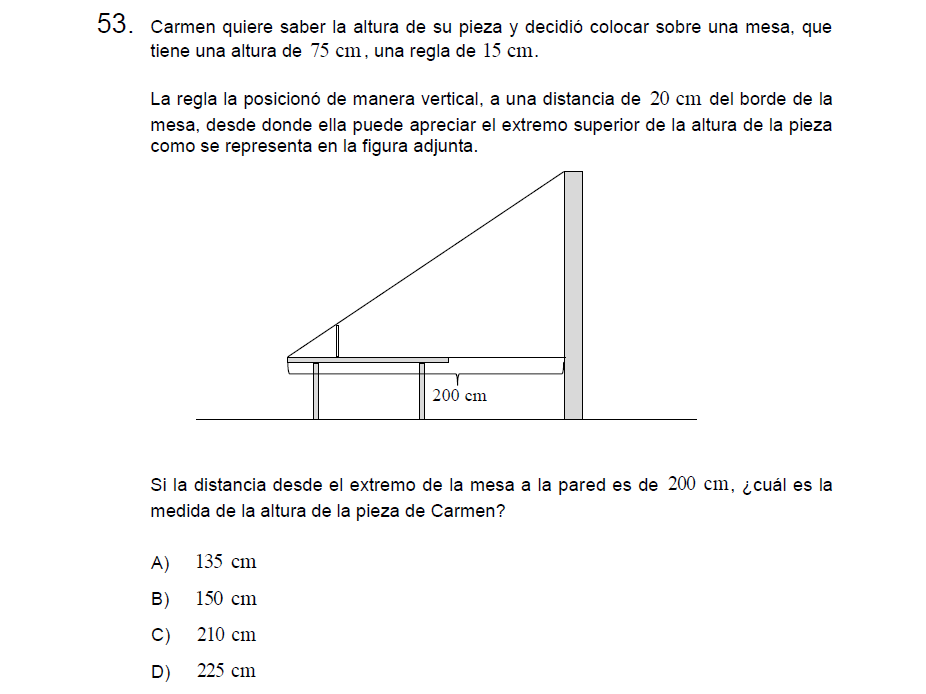
Solución:
Nuevamente resolveremos con semejanza de triángulos usando una proporción, nos fijamos en la base del triángulo pequeño, su alto y luego saltamos al triángulo más grande y su alto
\[\frac{alto}{base}=\frac{15}{20}=\frac{x}{200}\]
\[\frac{15}{20}=\frac{x}{200}\]
\[\frac{15\cdot 200}{20}=x\]
\[15\cdot 10=x\]
\[150=x\]
A esta altura debemos añadirle los 75 cm que tiene de alto la mesa!
\[150+75=225\]
Letra D.
P54
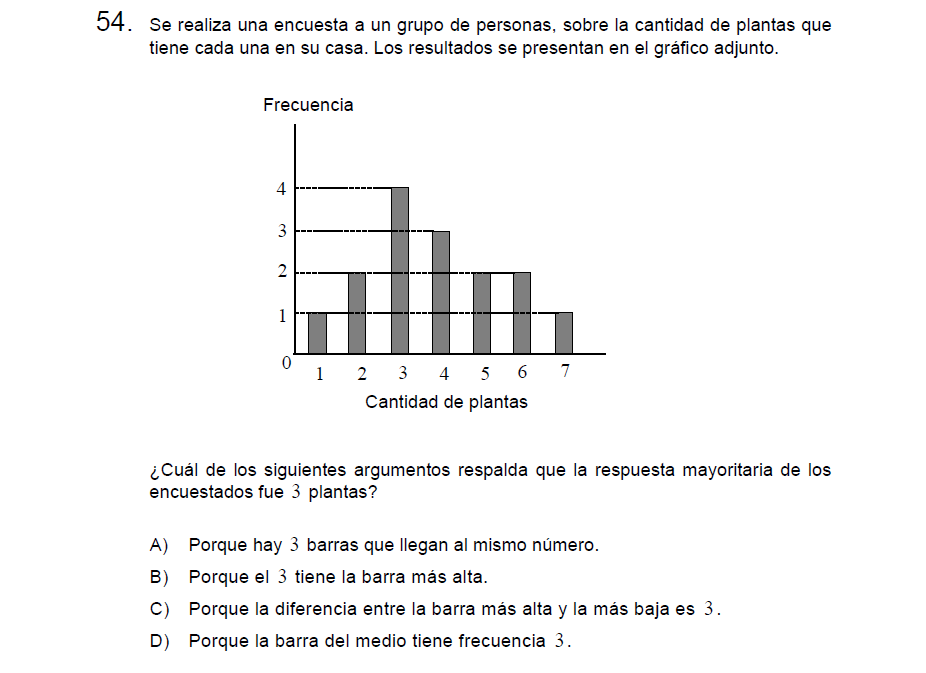
Solución:
Esta respuesta es prácticamente obvia, la única dificultad puede estar en entender qué es la frecuencia, sin embargo, esto hace alusión a la cantidad de personas que dijeron que tenían 3 plantas, en este caso fueron 4 personas la mayor cantidad de personas por respuesta.
Letra B.
P55

Solución:
Podemos aumentar un 20% a cada frecuencia y luego sumarlas
\[total=h\cdot 1,2 + 200 \cdot 1,2 + t\cdot 1,2 + 50\cdot 1,2\]
\[total=h\cdot 1,2 + 240 + t\cdot 1,2 + 60\]
\[total=300+ h\cdot 1,2 + t\cdot 1,2 \]
Letra A.
P56

Solución:
A. Falso ya que son barras independientes, es un resumen por año.
B. Falso, solo se nos habla de quienes comieron, nada se dice si lo disfrutaron :D.
C. Falso, no podemos asegurar que esto sea así, pareciera ser que esto va en aumento, sin embargo, como dije en A, son eventos independientes unos de otros.
D. Correcta, esto es correcto, sin embargo, no podemos asegurar que la tendencia se mantendrá.
Letra D.
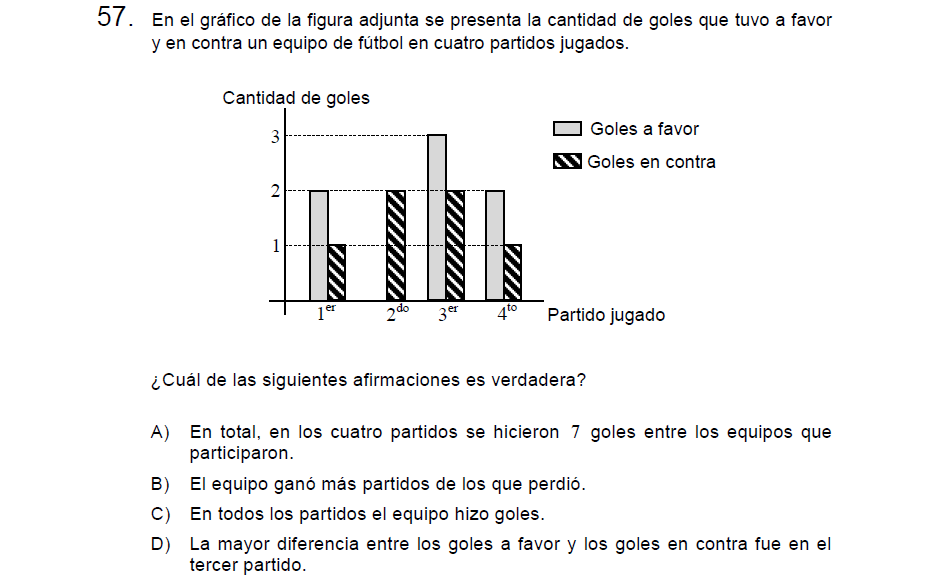
P57
Solución:
Veamos una a una
A. Sumando goles a favor y en contra tenemos 3 + 2 + 5 + 3 = 13. FALSA
B. El equipo ganó 3 partidos y perdió 1. VERDADERA.
C. En el segundo no hizo goles. FALSA.
D. Es solo de 1 gol la diferencia, en el segundo fue de 2. FALSA.
Letra B.
P58

Solución:
Podemos calcular la nota faltante (x) con la fórmula de promedio
\[\text{Promedio}=\frac{5.3+5.9+x}{3}\]
\[5.9=\frac{5.3+5.9+x}{3}\]
\[17.7=5.3+5.9+x\]
\[17.7=11.2+x\]
\[17.7-11.2=x\]
\[6.5=x\]
Letra D.
P59

Solución:
La totalidad de trabajadores corresponde a la suma de n, m y w. Esto iría en el denominador de la fórmula, para el numerador debemos multiplicar cada sueldo por la cantidad de personas que lo reciben y sumar dichas cantidades es decir
\[800.000\cdot n + 500.000 \cdot m+ 1.100.000 \cdot w\]
Finalmente nos quedaría
\[\frac{800.000\cdot n + 500.000 \cdot m+ 1.100.000 \cdot w}{n+m+w}\]
Letra D.
P60
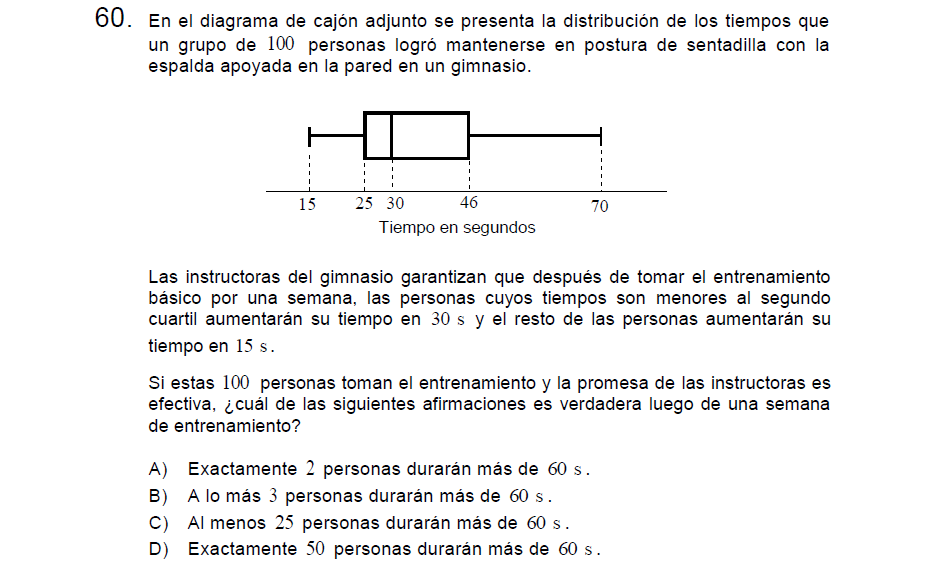
Solución:
Para resolver debemos recordar que el diagrama de caja agrupa los 25% de los datos ya que en él se representan los cuartiles (cada línea vertical de la caja), no podemos saber a ciencia cierta que valores son pero si entre que valores se encuentran.
Es así que un 25% de los datos es mayor o igual a 46, esto significa que por lo menos 25 personas están en este intervalo, si se asegura que ellos aumentaran 15 segundos su tiempo de resistencia, ya contamos con 25 personas que resistirán más de 60 segundos (61 por lo menos).
Con esto ya sabemos que la alternativa correcta es la
Letra C.
P61
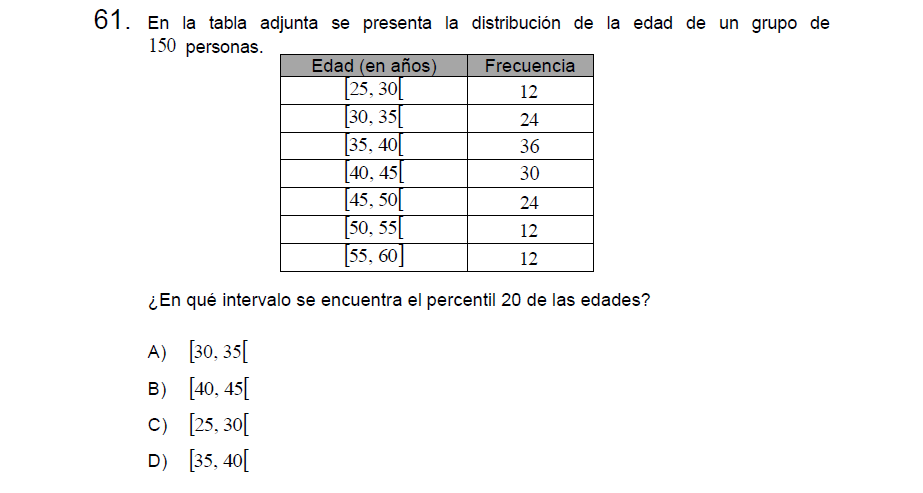
Solución:
Utilizamos la fórmula para determinar la posición del percentil 20
\[P_{20}=\frac{20}{100}\cdot 150\]
\[P_{20}=\frac{2}{1}\cdot 15\]
\[P_{20}=30\]
El dato se encuentra en la posición 30, en la primera fila tenemos 12 datos, en la segunda 24, si sumamos ambas tenemos un total de 36 datos, por lo tanto alcanzamos el dato 30 en la segunda fila, esto significa que se encuentra en el intervalo
\[[30,35[\]
Letra A.
P62
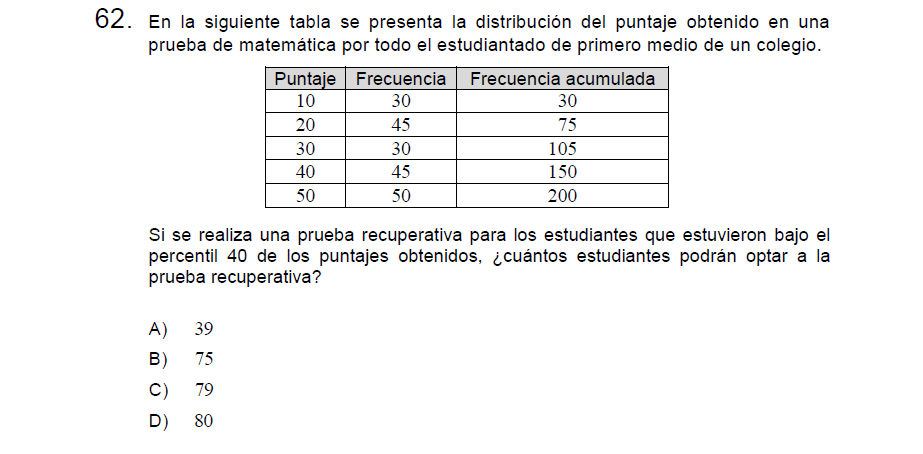
Solución:
En primer lugar debemos notar que el total de estudiantes es 200 (el número final de la columna de Frecuencia acumulada), con esto procedemos a determinar que posición ocupa el dato del percentil 40
\[P_{40}=\frac{40}{100}\cdot 200\]
\[P_{40}=\frac{40}{1}\cdot 2\]
\[P_{40}=80\]
El dato se ubica en la posición 80. Con esta información podemos observar nuevamente la columna de frecuencia acumulada y determinar en que fila se ubica el dato 80.
El dato 80 está en la tercera fila ya que en esa fila se tienen los datos de las posiciones «76 al 105»
Para determinar cuantos estudiantes están bajo este percentil «sumamos las frecuencias anteriores» o «vemos la frecuencia acumulada anterior» 75.
Letra B.
P63

Solución:
En primer lugar calcularemos las probabilidades por separado
Vainilla: \(P(V)=\frac{9}{50}\)
Frutilla: \(P(F)=\frac{6}{50}\)
Ahora debemos comprender lo solicitado, nos indican un sabor O el otro, por lo tanto debemos sumar ambas probabilidades, el único cuidado sería si tuvieran elementos en común (su intersección no fuera vacía), sin embargo, en este caso no los tienen, sumamos directamente
\[P(V)+P(F)=\frac{9}{50}+\frac{6}{50}=\frac{15}{50}=\frac{3}{10}\]
Letra A.
P64

Solución:
La probabilidad de que tenga menos de tres vocales es \(\frac{2}{3}\) por lo tanto, la probabilidad de que tenga tres vocales o más es \(\frac{1}{3}\).
Podemos amplificar las probabilidades por 2 para tener el espacio muestral completo (las 6 tarjetas) quedando
\[P(\text{menor que 3})=\frac{4}{6}\]
\[P(\text{mayor o igual que 3})=\frac{2}{6}\]
De aquí concluimos que 4 palabras tendrán menos de 3 vocales y 2 tendrán 3 o más, ya se nos han dado a conocer 3 palabras con menos de 3 vocales por lo tanto falta 1 más y también 1 palabra con 3 o más vocales.
Letra C.
P65

Solución:
Podemos resolver de varias maneras, pero aprovecharé de dejarles el espacio muestral de lanzar tres monedas (las posibles combinaciones)
\[\Omega={CCC, CCS, CSC, CSS, SCC, SCS, SSC, SSS}\]
Como pueden ver son 8 posibles combinaciones, de ellas nos piden «al menos», es decir, como mínimo (eso o más), lo cual sería 7 de 8
\[\frac{7}{8}\]
Letra B.
