Antes de comenzar le dedico esta resolución a todos y todas quienes deben rendir la Prueba M2, imagino que van por carreras matemáticas como ingeniería y otras.
Sé que pueden haber soluciones más simples o quizá se me pasó algún error, cualquier detalle por favor coméntenme :D, mucho éxito!
P1
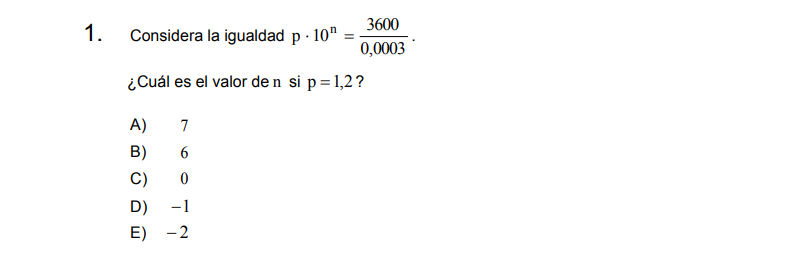
Solución:
\[p\cdot 10^n = \frac{3600}{0,0003}\]
Reemplazamos
\[1,2\cdot 10^n = \frac{3600}{0,0003}\]
Escribimos como potencia de 10
\[1,2\cdot 10^n = \frac{36\cdot 10^2}{3\cdot 10^{-4}}\]
Dividimos
\[1,2\cdot 10^n = 12\cdot 10^6\]
Añadimos una coma cambiando el exponente de la potencia
\[1,2\cdot 10^n = 1,2\cdot 10^7\]
\[n=7\]
Letra A.
P2

Solución:
\[10^6\cdot (T_6(\pi) – T_5(\pi))\]
Reemplazamos, basta con contar los decimales (6) y (5)
\[10^6\cdot(3,141592-3,14159)\]
Restamos, todo se cancela salvo el 2 del primer número
\[10^6\cdot(0,000002)\]
Multiplicamos, basta con correr la coma 6 espacios a la derecha
\[2\]
Letra C.
P3

Solución:
\[Á_o=\pi R^2=Á_c=P^2=Á_\Delta=\frac{PH}{2}\]
Elegimos e igualamos de a dos
\[Á_c=Á_\Delta \to P^2 = \frac{PH}{2}\]
\[ P^2 = \frac{PH}{2}\]
Despejamos H
\[\frac{2P^2}{P}=H\]
Simplificamos
\[2P=H\]
\[P<H\]
Igualamos las otras dos
\[Á_o=Á_c \to \pi R^2=P^2\]
\[\pi R^2=P^2\]
Despejamos
\[R^2=\frac{P^2}{\pi}\]
\[R<P\]
Letra E.
P4

Solución:
Nos toca probar con cada alternativa 🥺
A. \(\sqrt{2}+(-\sqrt{2})=0\not\in I\)
B. \(0(\sqrt{3}+\sqrt{2})=0\not\in I\)
C. \(\sqrt{\sqrt{2}+(-\sqrt{2})}=\sqrt{0}=0 \not\in I\)
E. \(\frac{-\sqrt{2}+0}{\sqrt{2}}=\frac{-\sqrt{2}}{\sqrt{2}}=-1 \not \in I\)
Letra D.
P5

Solución:
Explicación: Debemos recordar que multiplicar por 1 es equivalente al 100% y cualquier decimal por encima o por debajo se puede traducir en un aumento o disminución del porcentaje, es así que multiplicar por 1,3 un valor equivale a aumentarlo en 30% y multiplicar por 0,8 equivale a disminuirlo en 20%, el resultado está multiplicado por 1,04, es decir, aumentado en un 4%
\[\text{Largo} = L, \text{Ancho}=A\]
\[Á=LA\]
\[\text{Largo}=1,3L\]
\[\text{Ancho}=0,8A\]
\[Á=1,3L\cdot0,8A\]
\[Á=1,04LA\]
Variación de 4%
Letra C.
P6

Solución:
\[\sqrt[5]{a\cdot2a\cdot4a\cdot8a\cdot16a}=\]
\[\sqrt[5]{2\cdot2^2\cdot2^3\cdot2^4a^5}=\]
\[\sqrt[5]{2^{10}\cdot a^5}=\]
\[\sqrt[5]{2^{10}}\cdot \sqrt[5]{a^5}=\]
\[\sqrt[5]{2^{10}}\cdot a=\]
\[a\cdot \sqrt[5]{2^{10}}\]
Letra C.
P7

Solución:
A.
\[2r_A=2\sqrt[3]{\frac{3}{4\pi}V_A}\]
\[=\sqrt[3]{2^3 \cdot \frac{3}{4\pi}V_A}\]
\[=\sqrt[3]{\frac{3}{2\pi}V_A}\]
B.
No podemos sumar debido a que sus cantidades subradicales son distintas.
C.
\[\frac{r_A}{r_B}=\frac{\sqrt[3]{\frac{3}{4\pi}V_A}}{\sqrt[3]{\frac{3}{4\pi}V_B}}\]
\[=\sqrt[3]{\frac{\frac{3}{4\pi}V_A}{\frac{3}{4\pi}V_B}}\]
\[\sqrt[3]{\frac{V_A}{V_B}}\]
Letra C.
P8

Solución:
\[\sqrt{24p}+3\cdot\sqrt{150p}=\]
\[\sqrt{3\cdot2\cdot2\cdot2p}+3\cdot\sqrt{3\cdot5\cdot5\cdot2p}=\]
\[2\sqrt{3\cdot2p}+3\cdot 5\sqrt{3\cdot 2p}=\]
\[2\sqrt{6p}+15\sqrt{6p}=\]
\[17\sqrt{6p}\]
Letra D.
P9
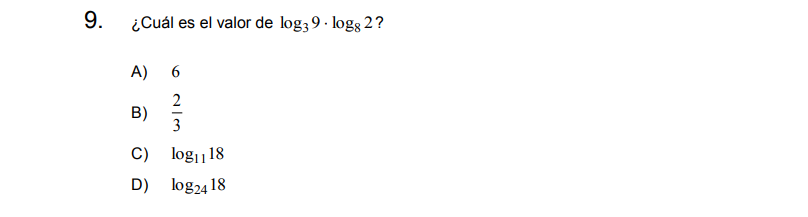
Solución:
\[log_39\cdot log_82=\]
\[2\cdot log_82=\]
\[(log_82\to 8^x = 2)\]
Resolvamos esto primero y luego regresemos
\[8^x=2\]
\[(2^3)^x=2^1\]
\[2^3x=2^1\]
(ecuación exponencial)
\[3x=1\]
\[x=\frac{1}{3}\]
volvamos
\[2\cdot log_82\]
\[2\cdot \frac{1}{3}=\]
\[\frac{2}{3}\]
Letra B.
P10

Solución:
La situación se modela con la expresión
\[C_F=C_I\cdot3^d=p\cdot3^d\]
\[d=0\to C_F=C_I=p\]
\[d=1\to C_F=3C_I=3p\]
\[d=2\to C_F=9C_I=3^2 \cdot p\]
\[d=3\to C_F=27C_I=3^3 \cdot p\]
\[d=4\to C_F=81C_I=3^4 \cdot p\]
\[d=5\to C_F=243C_I=3^5 \cdot p\]
Letra C.
P11

Solución:
\[log\sqrt{b^2-p^2}\]
\[=log(b^2-p^2)^{\frac{1}{2}}\]
\[=\frac{1}{2}log(b^2-p^2)\]
\[=\frac{1}{2}log((b+p)(b-p))\]
\[=\frac{1}{2}log(b+p)+\frac{1}{2}log(b-p)\]
\[=\frac{log(b+p)+log(b-p)}{2}\]
Letra E.
P12

Solución:
\[B=10\cdot log\frac{I}{I_0}\]
\[B=10\cdot log\frac{10^{-7}}{10^{-12}}\]
\[B=10\cdot log10^{-7-(-12)}\]
\[B=10\cdot 10^5\]
\[B=10\cdot 5 \cdot 1\]
\[B=50\]
Letra B.
P13

Solución:
\[log_mp=3\to m^3=p\]
\[log_p(m\cdot p^2)\]
\[log_{m^3}(m\cdot (m^3)^2)\]
\[log_{m^3}(m\cdot m^6)\]
\[=log_{m^3}m^7\to(m^3)^x=m^7\]
\[(m^3)^x=m^7\]
\[m^{3x}=m^7\to 3x=7\]
\[3x=7\]
\[x=\frac{7}{3}\]
Letra B
P14

Solución:
\[-3<a<3 \text{y} 1<b<8\]
\[a=2, b=2 \to \frac{2}{2}=1\]
Lo anterior descarta a C.
\[a=0, b=2 \to \frac{0}{2}=0\]
Lo anterior descarta a D.
\[a=-2.9, b=1.1 \to \frac{-2.9}{1.1}=-2.6\]
Lo anterior descarta a B.
Letra A.
P15

Solución:
\[h_1=\frac{d_1\cdot h_0}{d_0}\]
\[h_B=\frac{d_1\cdot h_0}{d_B}, h_T=\frac{d_1\cdot h_0}{d_T}\]
\[h_B=\frac{d_1\cdot 25}{200}, h_T=\frac{d_1\cdot 10}{250}\]
\[\frac{200\cdot h_B}{25}=d_1, \frac{250\cdot h_T}{10}=d_1\to\]
\[\frac{200\cdot h_B}{25}=\frac{250\cdot h_T}{10}\]
\[8\cdot h_B=25\cdot h_T\]
\[h_B=\frac{25}{8}h_T\]
Letra B.
P16

Solución:
En primer lugar, organizaremos la ecuación:
\[-px-qx=r\]
\[x(-p-q)=r\]
\[x=\frac{r}{(-p-q)}\]
\[x=\frac{r}{-(p+q)}\]
\[x=\frac{-r}{p+q}\]
\[\frac{-r}{p+q}\not \in R^+\]
Para que esta expresión pertenezca al conjunto solicitado, numerador y denominador deben ser del mismo signo, además numerador y denominador no pueden ser 0.
D.
\[-pr>qr\]
\[-pr-qr>0\]
\[-r(p+q)>0\]
Lo anterior coincide con nuestros numerador y denominador, además, nos indica que su multiplicación es positiva, por tanto, ambas expresiones poseen el mismo signo y no son 0.
Letra D.
P17

Solución:
Un sistema tiene infinitas soluciones cuando las ecuaciones son equivalentes, es decir, podemos transformar una en la otra por medio de multiplicar por algún factor. Esto puede escribirse además como:
\[\frac{30}{p}=\frac{q}{-3}=\frac{12}{2}\]
\[\frac{30}{p}=\frac{q}{-3}=6\]
\[q=6\cdot -3\]
\[q=-18\]
\[\frac{30}{p}=6\]
\[30=6\cdot p\]
\[\frac{30}{6}=p\]
\[5=p\]
Letra C.
P18

Solución:
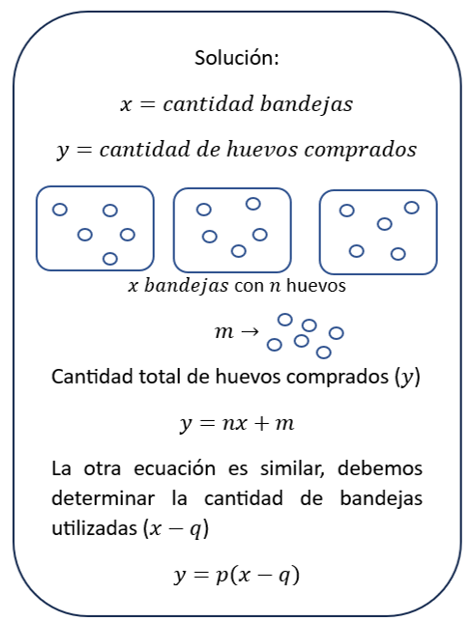
Letra A.
P19

Solución:
Un sistema de ecuaciones no tiene solución cuando las rectas que lo conforman son paralelas, esto se puede confirmar al observar sus pendientes (m)
\[y=mx+b\]
En este caso debemos decidir entre las alternativas A y B.
Podemos descartar la alternativa A porque es exactamente igual siendo rectas coincidentes (infinitas soluciones).
Letra B.
P20

Solución:
Antes de hacer un esquema debemos puntualizar que la gráfica de la función interseca al eje Y en el punto (0,4), esto nos da un triángulo cuyo cateto mide cuatro unidades, necesitamos otro que complete la ecuación del área:
\[12=\frac{4\cdot x}{2}\]
\[6=x\]
Por lo cual necesitamos un cateto de 6 unidades, este cateto tendría por extremo el punto de coordenadas (6,0), con estos puntos podemos formar la ecuación de la recta:
\[y-y_1=\frac{y_2-y_1}{x_2-x_1}(x-x_1)\]
\[y-4=\frac{0-4}{6-0}(x-0)\]
\[y-4=\frac{-4}{6}x\]
\[y=\frac{-2}{3}x+4\]
\[m=-\frac{2}{3}\]
Letra D.
P21

Solución:
La distancia entre los puntos A y B puede ser obtenida utilizando el teorema de Pitágoras, para ello tomamos como referencia el punto de partida P.
\[d(AB)=\sqrt{d(AP)^2+d(BP)^2}\]
La distancia recorrida por el vehículo A puede ser modelada como \(d(AP)=60t\) y la distancia recorrida por el vehículo B puede ser modelada como \(d(BP)=80t\), de este modo se tiene
\[d(AB)=\sqrt{(60t)^2+(80t)^2}\]
\[d(AB)=\sqrt{3600t^2+6400t^2}\]
\[d(AB)=\sqrt{10.000t^2}\]
\[d(AB)=100t\]
Letra B.
P22

Solución:
El consumo de combustible bajo condiciones constantes se puede obtener a partir de la fórmula
\[\text{Consumo}=\frac{\text{Distancia}}{\text{Litros}}\]
Reemplazando las letras del enunciado sería:
\[\text{Consumo}=\frac{x}{M}\]
Letra A.
P23

Solución:
\[\text{Área de un tríangulo}=\frac{\text{base}\cdot \text{altura}}{2}\]
\[39=\frac{b\cdot (b+7)}{2}\]
\[78=b\cdot (b+7)\]
\[78=b^2+7b\]
\[0=b^2+7b-78\]
Letra
P24

Solución:
Para resolver debemos despejar el tiempo (t), donde \(f(t)=0\)
\[0=-t^2+2t+120\]
\[0=t^2-2t-120\]
\[0=(t+10)(t-12)\]
\[t_1=-10\]
\[t_2=12\]
Letra C.
P25

Solución:

Letra A.
P26

Solución:
Para que la ecuación tenga única solución, su discriminante debe ser igual a 0, es decir,
\[\Delta=b^2-4ac=0\]
\[a=1, b=k, c=9\]
\[\Delta=(k)^2-4\cdot 1\cdot9=0\]
\[k^2-36=0\]
\[(k+6)(k-6)=0\]
\[k_1=-6\]
\[k_2=6\]
Letra A.
P27

Solución:
\[(x_1+1)(x_2+1)\]
\[x_1\cdot x_2+x_1+x_2+1\]
Recordar las propiedades:
\[x_1\cdot x_2=\frac{c}{a}\]
\[x_1+x_2=\frac{-b}{a}\]
Reemplazamos los coeficientes de la ecuación
\[\frac{-k}{2}-\frac{k}{2}+1=\]
\[-\frac{2k}{2}+1=\]
\[-k+1\]
Letra B.
P28

Solución:
Podemos igualar la expresión a 40 para determinar el momento en que llega a esa temperatura o bien plantear una inecuación, sin embargo, considero que lo más rápido es probar evaluando las alternativas
A. \(T(0)=-4(0)^2+24(0)+40=40\)
B. \(T(2)=-4(2)^2+24(2)+40=72\)
C. \(T(3)=-4(3)^2+24(3)+40=76\)
D. \(T(6)=-4(6)^2+24(6)+40=40\)
Letra D.
P29

Solución:
Recordemos que el producto de las soluciones de una ecuación cuadrática es igual a \(\frac{c}{a}\)
\[qx^2+(q-2)x-2q-1=0\]
\[c=-2q-1\]
\[a=q\]
\[\frac{c}{a}=\frac{-2q-1}{q}=-4\]
\[\frac{-2q-1}{q}=-4\]
\[-2q-1=-4q\]
\[-2q+4q=1\]
\[2q=1\]
\[q=\frac{1}{2}\]
Letra D.
P30

Solución:
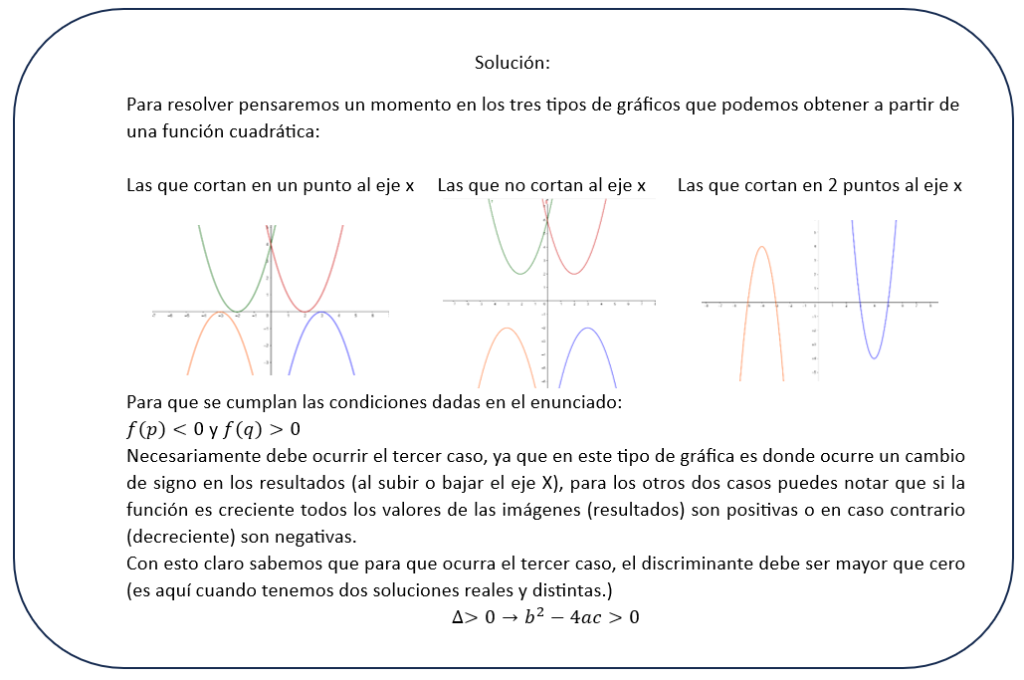
Letra B.
P31

Solución:
Aclaración: Debemos determinar la distancia (separación) entre los puntos de intercepción (soluciones), esta parábola tiene su vértice en el eje Y por lo cual nos aprovecharemos de la simetría de la parábola para ahorrarnos un cálculo, es decir, si obtenemos la distancia desde el origen hacia una solución, la otra medirá lo mismo.
Por último, el coeficiente b es positivo, ya que no puede ser 0 (de lo contrario no sería función cuadrática) y no puede ser negativo ya que, de ser así, la parábola abriría hacia abajo sin interceptar al eje X (ya que su vértice está en (0,-4).
Determinemos la coordenada x del punto solución
\[f(x)=bx^2-4\]
\[0=bx^2-4\]
\[4=bx^2\]
\[\frac{4}{b}=x^2\]
\[\sqrt{\frac{4}{b}}=x\]
\[\frac{2}{\sqrt{b}}=x\]
Ahora multiplicamos por 2 está expresión y determinamos cuando será mayor a 4.
\[2\cdot \frac{2}{\sqrt{b}}>4\]
\[\frac{4}{\sqrt{b}}>4\]
\[\frac{16}{b}>16\]
\[\frac{16}{16}>b\]
\[1>b\]
Acorde con la explicación previa la solución será
]0,1[
Letra B.
P32
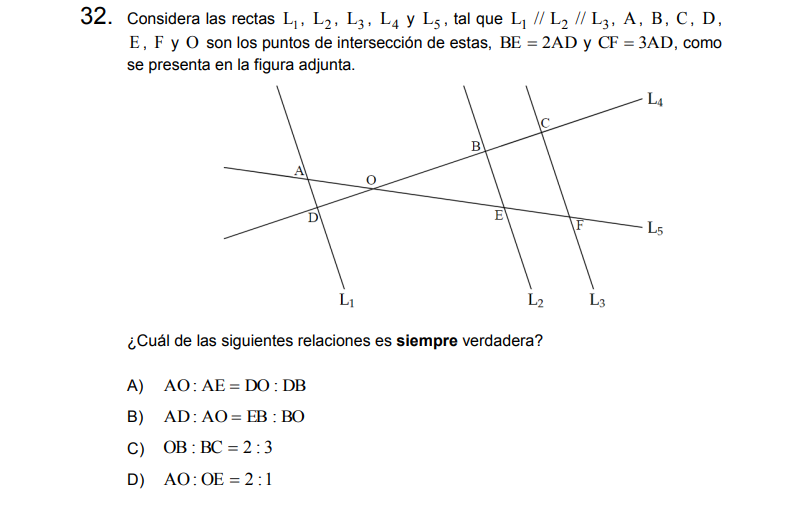
Solución:
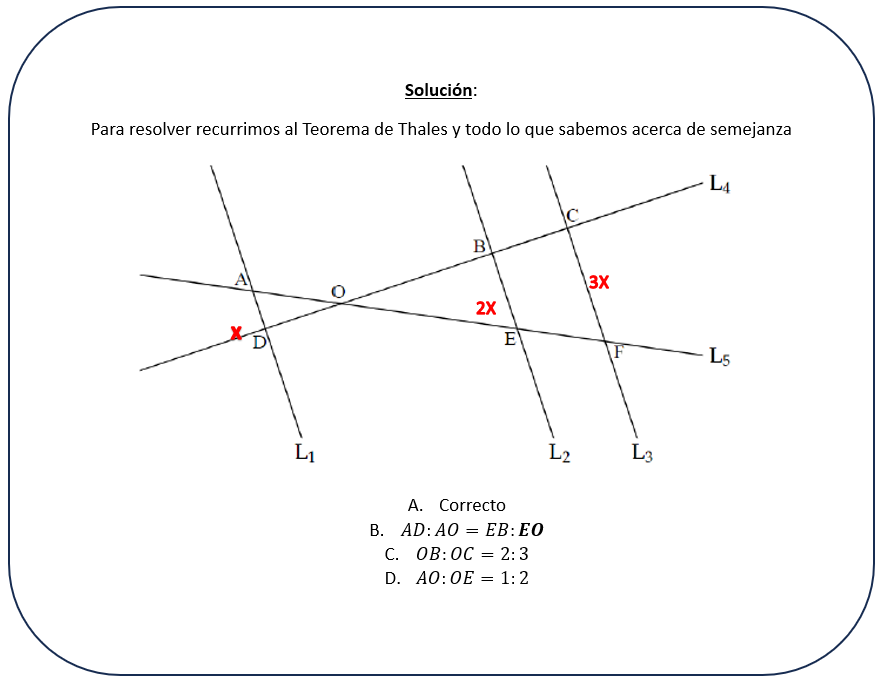
Letra A.
P33

Solución:
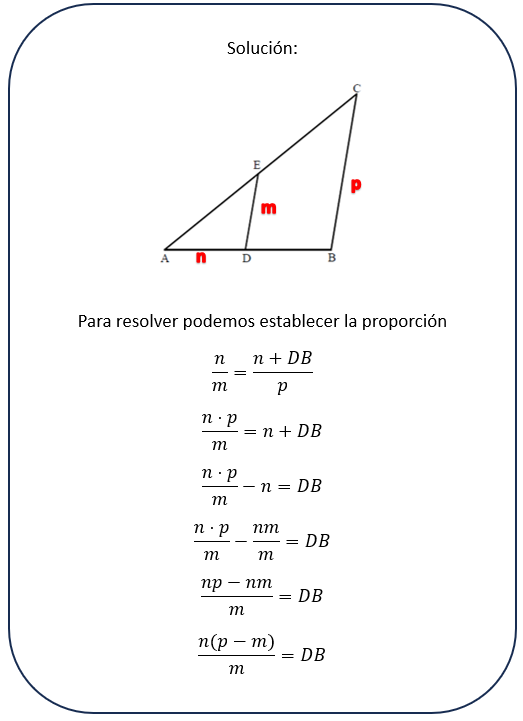
P34

Solución:

Letra B.
P35

Solución:
Determinemos en primer lugar las expresiones de las medidas del segundo rectángulo
\[\frac{AD}{EH}=\frac{2}{3}\]
\[\frac{\frac{a}{2}}{EH}=\frac{2}{3}\]
\[\frac{3\cdot \frac{a}{2}}{2}=EH\]
\[3\cdot \frac{a}{2}\cdot \frac{1}{2}=EH\]
\[\frac{3a}{4}=EH\]
Obtengamos el otro lado
\[\frac{EH}{AD}=\frac{EF}{AB}\]
\[\frac{\frac{3a}{4}}{\frac{a}{2}}=\frac{EF}{5b}\]
\[\frac{\frac{3a}{4}\cdot 5b}{\frac{a}{2}}=EF\]
\[\frac{3}{4}\cdot 5b \cdot 2 = EF\]
\[\frac{3}{2}\cdot 5b \cdot 1 = EF\]
\[\frac{15b}{2}=EF\]
Saquemos el área
\[Á=EF\cdot EH\]
\[Á=\frac{15b}{2}\cdot \frac{3a}{4}\]
\[Á=\frac{45ab}{8}\]
Letra E.
P36

Solución:
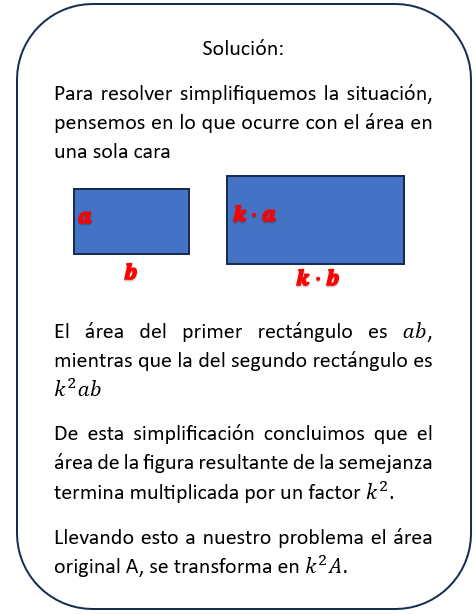
Letra D.
P37

Solución:
Para resolver basta con reemplazar los datos otorgados en la expresión y despejar lo solicitado
\[H=kh\]
\[500=2.5\cdot h\]
\[\frac{500}{2.5}=h\]
\[\frac{5000}{25}=h\]
\[200=h\]
Letra B.
P38

Solución:
Letra C.
P39

Solución:
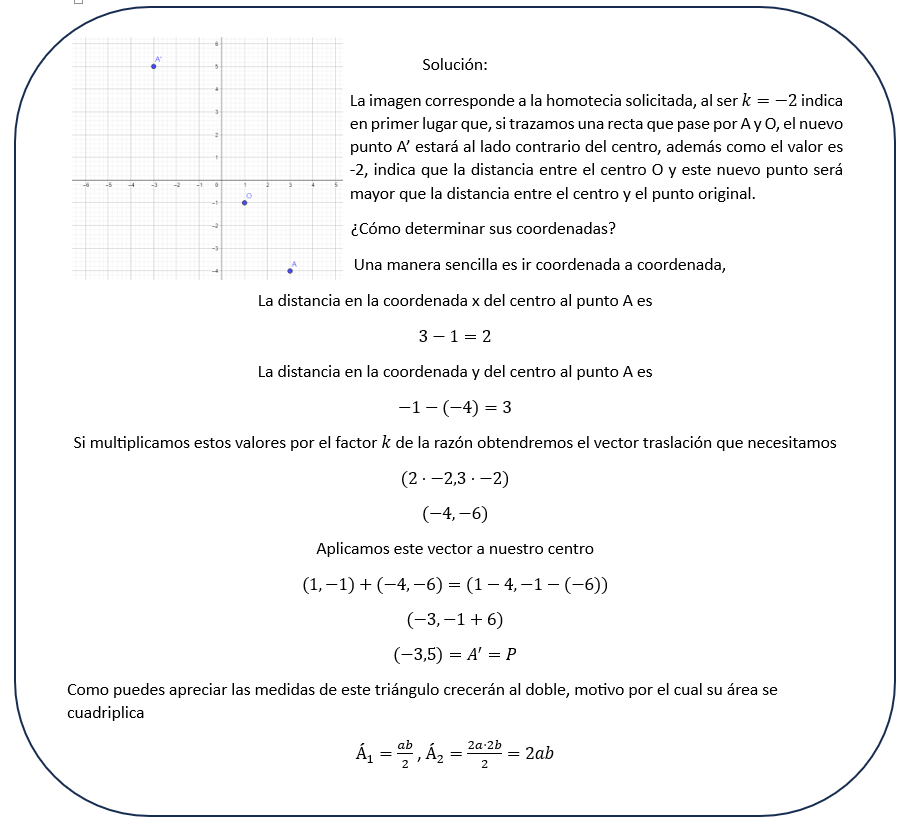
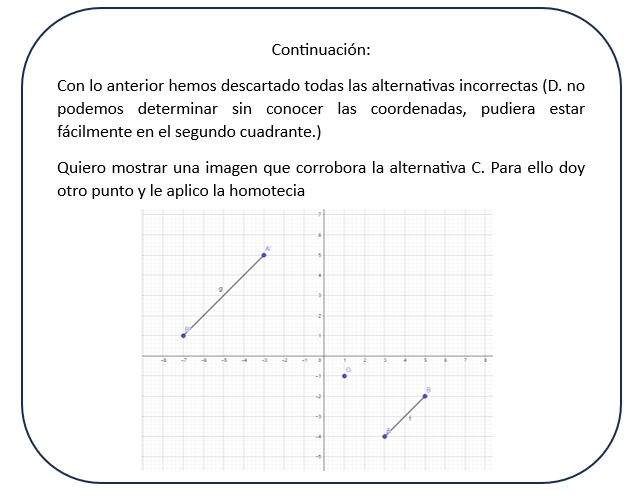
A. Si la razón es positiva indica dos cosas, que la figura resultante está en el mismo lado con respecto al centro de homotecia (primer cuadrante) y que la figura es mas grande o más pequeña dependiendo del valor de la razón de homotecia.
Si \(r>1\), la figura resultante es más grande.
Si \(0<r<1\), entonces la figura resultante es más pequeña.
B. Esto sería verdad si \(r>1\), lo cual no sabemos.
C. Esto sería verdad si \(r>1\), lo cual no sabemos.
D. Esto podría darse cuando \(r=1\)
Letra A.
P40

Solución:

Letra E.
P41
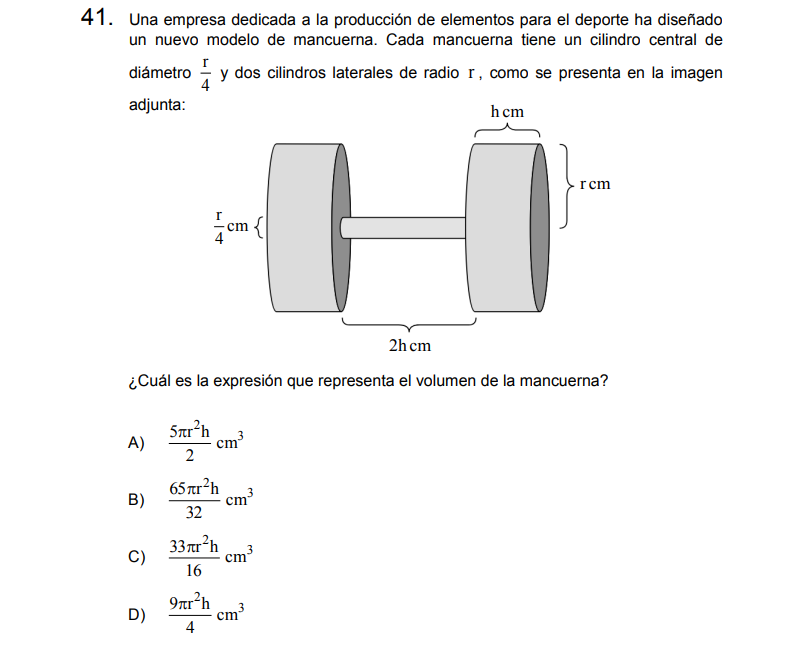
Solución:

Letra B.
P42

Solución:
Paso 1. Correcto ya que \(tan(55°=\frac{CD}{10})\), luego se reemplazó el valor y se dividió.
Paso 2. Con el valor de CD se procede a usar \(sen(55°)=\frac{CD}{CB}\), se reemplazan ambos valores y se divide.
Paso 3. La ecuación planteada es correcta ya que el ángulo CDA es recto y por lo tanto faltan 90° para formar los 180° del triángulo.
Paso 4. Al plantear la razón trigonométrica se comete el error ya que debería ser \(sen(20°)=\frac{CD}{AC}\to\)
\[0.34=\frac{14.2}{AC}\]
\[AC=\frac{14.2}{0.34}\]
\[AC=41.76\]
Utilizando el Teorema de Pitágoras obtenemos AD
\[\sqrt{(AC)^2-(CD)^2}=AD\]
\[\sqrt{1743.9-201.6}=AD\]
\[\sqrt{1541.4}=AD\]
\[39.2\approx AD\]
Luego AB es igual a
\[39.2+10=AB\]
\[49.2=AB\]
Letra D.
P43

Solución:
Para construir un diagrama de caja necesitamos determinar cada uno de los cuartiles, lo haremos por medio de su equivalencia con los percentiles considerando que tenemos un total de 24 datos (solamente los que no lograron eximirse)
\[p_{25}=\frac{25\cdot 24}{100}=\frac{1}{4}\cdot 24 = 6\]
Esto significa que el dato en la posición 6 corresponde al primer cuartil y por lo tanto el dato 12 y 18 corresponden al segundo y tercer cuartil respectivamente.
\[Q_1=43\]
\[Q_2=51\]
\[Q_3=63\]
Letra B.
P44

Solución:

Letra C.
P45

Solución:
Antes de plantear las probabilidades debemos notar que cada tipo de cartas tiene un cuarto del total de cartas, es decir,
\[\frac{m}{4}\]
Probabilidad en la Primera extracción
\[P(B)=\frac{\frac{m}{4}}{m}=\frac{m}{4}\cdot \frac{1}{m}=\frac{1}{4}\]
Probabilidad en la Segunda extracción (hay una carta menos)
\[P(B)=\frac{\frac{m}{4}-1}{m-1}\]
Ahora multiplicamos ambas probabilidades
\[\frac{1}{4}\cdot \frac{\frac{m}{4}-1}{m-1}\]
Letra D.
P46

Solución:
La probabilidad de extraer una bolita azul en la urna A es de
\[P(A)=\frac{m}{x}\]
Por lo tanto, la probabilidad de que NO sea azul en esta urna es de
\[1-P(A)=1-\frac{m}{x}=\frac{x-m}{x}\]
Repetimos el proceso para la otra urna. La probabilidad de extraer una bolita azul en la urna B es de
\[P(B)=\frac{n}{y}\]
Por lo tanto, la probabilidad de que NO sea azul en esta urna es de
\[1-P(B)=1-\frac{n}{y}=\frac{y-n}{y}\]
Con esto la probabilidad de que ninguna sea azul es de
\[\frac{x-m}{x}\cdot \frac{y-n}{y}\]
Letra A.
P47

Solución:

Letra D.
P48

Solución:
Sabiendo que la probabilidad de que
- el producto devuelto lo haya sido antes de la primera semana = N
- el producto tenga reparación, dado que fue devuelto antes de la primera semana de uso = M
la resolución del problema implica el planteamiento de una probabilidad condicional
- \(P(A\cap B)=?\)
- \(P(A/B)=M\)
- \(P(B):N\)
\[P(A/B)=\frac{P(A\cap B)}{P(B)}\]
\[M=\frac{P(A\cap B)}{N}\]
\[M\cdot N=P(A\cap B)\]
Letra B.
P49

Solución:
Los múltiplos de 5 son aquellos números que terminan en 0 o 5, lo cual nos fija el dígito 0 al final de la secuencia. No se nos indica que no podamos repetir cifras, por lo cual podríamos tener algo como 110 y finalmente debemos descartar que el dígito 0 quede en primera posición, quedando algo como
\[\text{_ _ 0}\]
- 3 opciones para el primer digito: {1,2,4}
- 4 opciones para el segundo dígito: {0,1,2,4}
- 1 opción para el último: {0}
Utilizando el principio multiplicativo, la expresión será
\[3\cdot 4\cdot 1\]
Letra D.
P50

Solución:
Para resolver podemos hacernos las siguientes preguntas
- ¿Se utilizan todos los elementos para formar los grupos?: NO, porque formamos grupos de a dos.
- ¿Importa el orden en que se formen los grupos?: NO, porque para este caso es el mismo grupo si sale vainilla-chocolate que chocolate-vainilla.
- ¿Se repiten los elementos?: NO, porque todos los sabores son distintos.
Con estas respuestas podemos concluir que debemos realizar una combinación \(C_2^6=\frac{6!}{(6-2)!\cdot2!}\)
\[\frac{6!}{(6-2)!\cdot 2!}=\]
\[\frac{6\cdot5\cdot4!}{4!\cdot 2\cdot 1}=\]
\[\frac{6\cdot 5}{2}=\]
\[3\cdot 5=15\]
Letra C.
P51

Solución:

Letra D.
P52

Solución:

Letra D.
P53

Solución:


Letra C.
P54

Solución:
- Con esta información conocemos que está sobre el percentil 10, es decir, sobre el 10% de personas de menor ingreso, sin embargo, en este rango pudiera pertenecer a cualquiera de los distintos tramos.
- Al saber que está bajo el cuartil 1, sabemos que el ingreso de la familia está bajo el 25% de las familias, por lo tanto, podemos ubicarla en el tramo 1.
Letra B.
P55

Solución:
\[M=P+Q\]
Para saber la cantidad de comisiones que se pueden conformar necesitamos elegir una cantidad P de mujeres del total de mujeres del curso y una cantidad Q de hombres del total del curso, asumiendo que una comisión es una muestra del total de estudiantes, por lo tanto formaremos grupos de estudiantes de un total, esto nos lleva a pensar en una combinación, para resolver una combinación necesitamos conocer la totalidad de personas de cada sexo y cuantas personas conforman las comisiones, por ejemplo:
De un total de 18 hombres se seleccionan 5 para la comisión \(C^{18}_5\), veamos nuestro problema.
- Con el valor M sabemos cuántas personas conforman la comisión, adicionalmente nos dan el número total de mujeres del curso, pero, no sabemos la cantidad de mujeres que estarán en la comisión y como no sabemos cuántos estudiantes hay en el curso tampoco podemos determinar la cantidad de hombres.
- Con P y Q sabemos la cantidad de hombres y mujeres que conforman los grupos, sin embargo, no sabemos la totalidad de estudiantes de cada sexo desde los cuales podemos elegir.
- Con ambas juntas conocemos la cantidad de estudiantes para conformar los grupos, conocemos la totalidad de mujeres, pero no conocemos la totalidad de hombres.
Letra E.
