Antes de comenzar quisiera saludar a mis alumnos y alumnas de 4to medio que rendirán la prueba este año, este post va con mucho cariño para ustedes, esperando que les sea de ayuda y logren sus metas!
Importante: Este material es de autoría del DEMRE yo solamente comparto mis resoluciones personales.
Pregunta n° 1

Solución:
Para obtener el mayor resultado, debemos restar la menor cantidad posible a 200, como debe ser de dos dígitos solo puede ser el número 10, por lo tanto:
\[200-10 = 190\]
Ahora lo multiplicamos por 2 (duplicar)
\[= 190\cdot 2\]
\[= 380\]
Letra C.
Pregunta n° 2

Solución: Podemos resolver de varias maneras, yo me apoyaré en notación científica para hacerlo más simple, por lo tanto:
\[\frac{(0,002)(0,02)}{0,01}=\]
\[\frac{(2\cdot 10^{-3})(2\cdot 10^{-2})}{1\cdot10^{-2}}=\]
multiplicamos los 2 y las potencias de 10 (se conserva la base y suman los exponentes)
\[\frac{(4\cdot 10^{-5})}{1\cdot10^{-2}}=\]
ahora dividimos las potencias de 10 (se conserva la base y restan los exponentes (-5 -(-2))
\[4\cdot 10^{-3}=\]
deshacemos la notación y nos queda
\[0,004\]
Letra B
Pregunta n° 3

Solución: para este ejercicio recordar que si la base de la potencia es negativa y el exponente es par el resultado es positivo, por lo tanto
\[1^2+(-1)^2+(0,1)^2=\]
\[1+1+(0,1)^2=\]
ahora solo falta resolver la potencia de \(0,1 (0,1 \cdot 0,1)\)
\[1+1+(0,1)\cdot(0,1)=\]
\[1+1+\frac{1}{10}\cdot \frac{1}{10}=\]
\[1+1+\frac{1}{100}=\]
\[2+0,01=\]
\[2,01\]
Letra C
Pregunta n° 4

Solución: tres números enteros se pueden escribir como
\[n, n+1, n+2\]
y su suma será
\[n + n+1 + n+2 = p\]
\[3n + 3 = p\]
la expresión anterior puede ser factorizada por 3 que es un término en común
\[3(n + 1) = p\]
de lo anterior podemos deducir que (p) es un múltiplo de 3. También podríamos dar valores para invalidar las otras opciones, por ejemplo, (-1 + 0 + 1 = 0) lo cual invalida la D.
Letra B.
Pregunta n° 5

Solución: para resolver este problema lo más sencillo es probar con las alternativas, si pagamos 9 meses, son:
\[9\cdot 10.000 = 90.000\]
por lo tanto 9 meses sigue siendo más económico que los 12 meses.
Letra A.
Pregunta n° 6
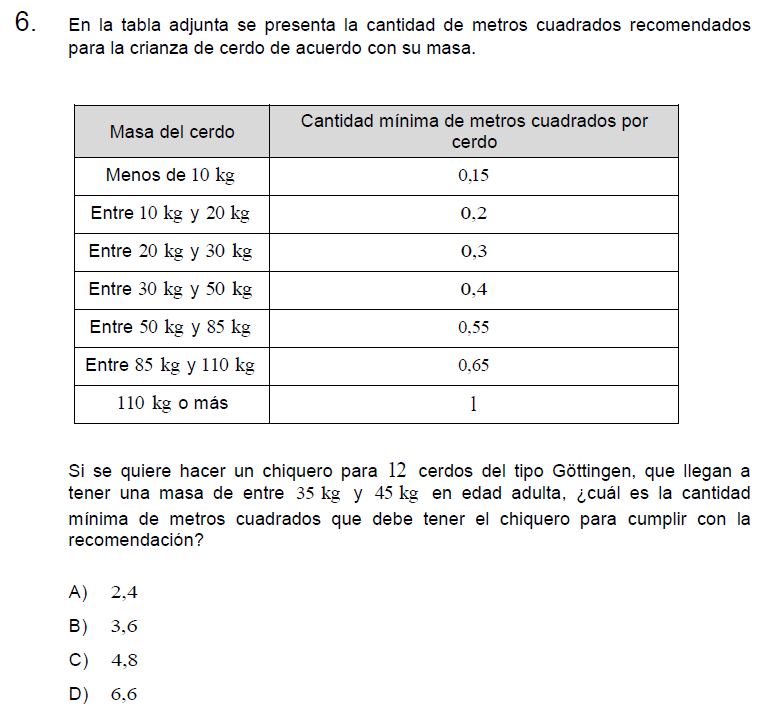
Solución: debemos ubicar en la tabla la fila que corresponda a los kilos mencionados, en este caso de 30 a 50 kg, luego multiplicamos la cantidad de cerdos por el espacio recomendado.
\[0,4 \cdot 12 =\]
para hacerlo simple multiplicamos 4 por 12 y luego dividimos por 10. (Ustedes multipliquen como gusten)
\[4 \cdot 12 = 48\]
\[48 : 10 = 4,8\]
Letra C.
Pregunta n° 7

Solución: para encontrar la cantidad original iremos retrocediendo, es decir, partimos desde los 70 y realizamos las operaciones contrarias a las mencionadas.
\[70\]
\[70-1=69\]
\[69-3=66\]
\[66+4=70\]
\[70-2=68\]
Letra B.
Pregunta n° 8

Solución: primero determinamos cuantos grados de diferencia hay entre las dos temperaturas, para hacerlo restamos, y luego dividimos esta cantidad en 3, de esta manera sabremos cuantas veces han transcurrido los 5 minutos. Por último multiplicamos esta cantidad por 5.
\[12 – (-36)=\]
\[12 + 36=48\]
\[48 : 3= 16\]
\[16\cdot 5 = 80\]
Letra B.
Pregunta n° 9

Solución: La razón de los tres días es 1:1:2 respectivamente, este tipo de ejercicios suelo considerarlos como partes de un todo, es decir, tenemos en total 4 partes de las cuales 1 es de matemática, 1 de física y 2 de lenguaje. Con esto podremos plantear una ecuación para determinar a cuanto equivale cada parte.
\[1x+1x+2x=3\text{horas}\]
\[4x=3\]
\[x=\frac{3}{4}\]
Nos queda un último problema que es transformar las horas a minutos y así coincidir con las alternativas.
\[\frac{3}{4}\cdot 60 = 45\]
Letra C.
Pregunta n° 10

Solución: Este tipo de problemas relaciona el resultado anterior con el factor de cambio, es decir, multiplicaremos las alturas por \(\frac{4}{5}\) sucesivamente.
El entero más cercano sería 51 cm
Letra A.
Pregunta n° 11

Solución: Cuando enseño a calcular porcentajes lo hago de varias maneras, la que más suele resultar es multiplicar los porcentajes en su forma de fracciones, es decir:
\[\frac{1}{100}\cdot \frac{200}{100}\cdot 200=\]
\[\frac{2}{100}\cdot 200=\]
\[2\cdot 2=\]
\[4\]
Letra B.
Pregunta n° 12

Solución: Determinamos primeramente los múltiplos (tabla) del 8 y luego calculamos que porcentaje son de los 50.
\[8; 16; 24; 32; 40; 48\]
Son 6 números de un total de 50, calcularemos el porcentaje utilizando una proporción:
\[\frac{porcentaje}{cantidad}=\frac{100}{50}=\frac{x}{6}\]
Es muy importante mantener el orden lateral al plantear la proporción (los porcentajes y las cantidades en la misma línea)
\[\frac{100}{50}=\frac{x}{6}\]
\[\frac{100\cdot 6}{50}=x\]
\[\frac{600}{50}=x\]
\[12=x\]
Letra B.
Pregunta n° 13

Solución: Para resolver pensaremos en el porcentaje que queda luego del proceso de purificación, es decir, restamos el 12% de los 100, quedando 88%. Ahora calculamos el 88% de los 2000.
\[\frac{2000}{100}=\frac{x}{88}\]
\[\frac{2000\cdot 88}{100}=x\]
\[\frac{20\cdot 88}{1}=x\]
\[20\cdot 88=x\]
\[1760=x\]
Letra C.
Pregunta n° 14

Solución: Determinaremos las horas que inicialmente eran destinadas a los comerciales, una vez hecho le añadiremos 2 horas y realizaremos nuevamente el cálculo del porcentaje.
\[\frac{x}{15}=\frac{24}{100}\]
\[x=\frac{24\cdot 15}{100}\]
\[x=\frac{360}{100}\]
\[x=3,6\]
Ahora le añadimos las 2 horas extras,
\[3,6+2=5,6\]
Finalmente calculamos el nuevo porcentaje,
\[\frac{x}{5,6}=\frac{100}{24}\]
\[x=\frac{100\cdot 5,6}{24}\]
\[x=\frac{560}{24}\]
\[x=23,\bar{3}\]
Letra C.
Pregunta n° 15

Solución: Para resolver este problema aplicaremos dos descuentos sucesivos, ojo, deben hacerlo paso a paso y NO sumar ambos porcentajes para sacarlo de una vez.
Primer descuento:
\[\frac{1500}{100}=\frac{x}{80}\]
\[\frac{1500\cdot 80}{100}=x\]
\[15\cdot 80=x\]
\[1200=x\]
Ahora vamos por el, Segundo descuento:
\[\frac{1200}{100}=\frac{x}{70}\]
\[\frac{1200\cdot 70}{100}=x\]
\[12 \cdot 70=x\]
\[840=x\]
Letra B.
Pregunta n° 16

Solución: Para resolver el problema debemos calcular primeramente el 20% de aumento sobre los 1800, con esto tendremos el nuevo precio del kilo de pan, una vez lo tengamos, la expresión final será VALOR x Kilogramos.
Para calcular el aumento podemos hacerlo de dos maneras, sacando el 20% y sumando ese resultado a los 1800 o sacando directamente el 120% de los 1800. Yo utilizaré el segundo método.
\[\frac{1800}{100}=\frac{x}{120}\]
\[\frac{1800\cdot 120}{100}=x\]
\[18\cdot 120=x\]
\[2160=x\]
La expresión corresponde entonces a \(2160\cdot x\)
Letra D.
Pregunta n° 17
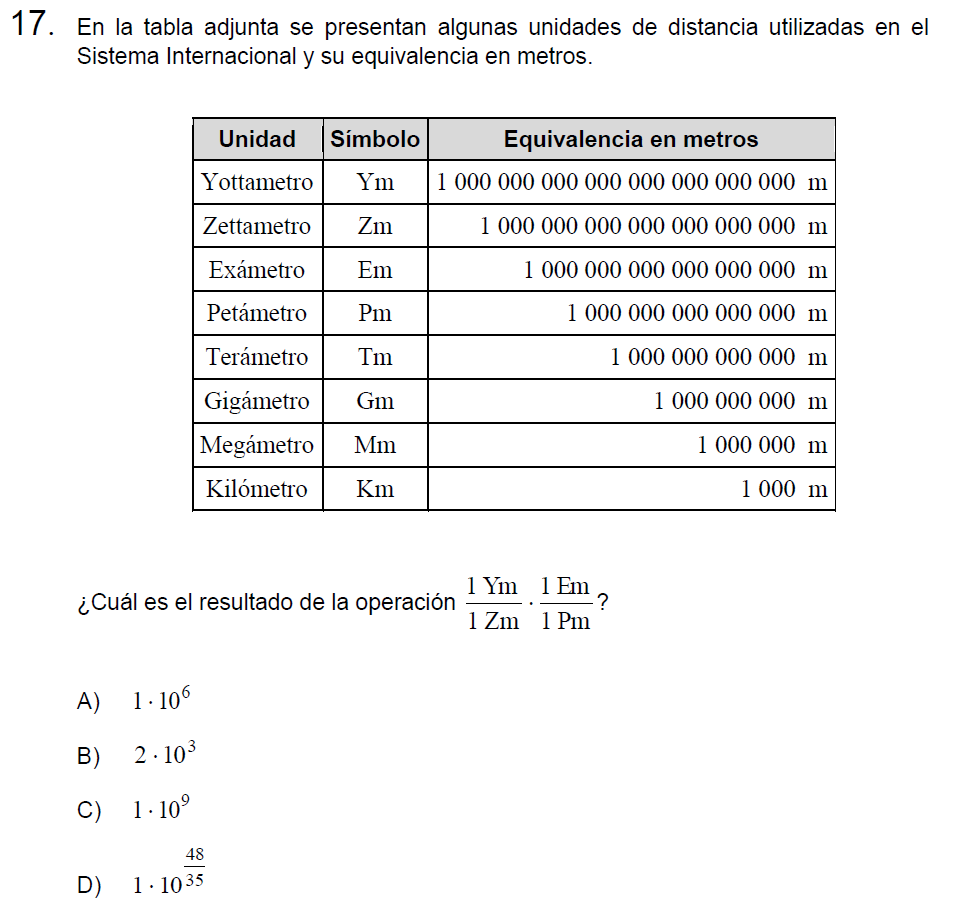
Solución: Para resolver, reemplazaremos el equivalente a cada Unidad en notación científica (recuerden que es colocar un 1 multiplicado por 10 elevado a la cantidad de 0 que tenga, por lo tanto es solo contar) y luego simplificamos.
\[\frac{1\cdot 10^{24}}{1\cdot 10^{21}}\cdot \frac{1\cdot 10^{18}}{1\cdot 10^{15}}\]
\[ 1\cdot 10^{3}\cdot 1\cdot 10^{3}=\]
\[ 1\cdot 10^{6}\]
Letra A.
Pregunta n° 18

Solución: Tenemos una división de potencias de igual base, se conserva la base y se restan los exponentes \(6-8=-2\).
Luego \(2^{-2}=\frac{1}{2^2}\).
Otra forma de resolver es pensar en la resta \(8-6\) y luego dejar el resultado en el lugar donde se tenía el número más grande (en el denominador).
Letra A.
Pregunta n° 19

Solución: La pregunta nos invita a probar con las alternativas, pero quizá podamos reescribir la expresión de una manera más sencilla.
\[\frac{(\frac{2}{3})^5}{(\frac{8}{15})^3}=\]
\[\frac{(\frac{2}{3})^3\cdot (\frac{2}{3})^2 }{(\frac{8}{15})^3}=\]
Ahora podemos dividir, ya que tenemos división de potencias de igual exponente (se conserva el exponente y dividen las bases (es una división de fracciones se mantiene la primera y se multiplica por la segunda invertida))
\[(\frac{2}{3}\cdot \frac{15}{8})^3\cdot (\frac{2}{3})^2 =\]
\[(\frac{5}{4})^3\cdot (\frac{2}{3})^2 =\]
\[\frac{125}{64}\cdot \frac{4}{9}= E\]
El valor anterior es E, ahora probaremos con las alternativas (aunque iré directo a la correcta)
\[144\cdot E=\]
\[144\cdot \frac{125}{64}\cdot \frac{4}{9}\]
\[16\cdot \frac{125}{64}\cdot 4=\]
\[16\cdot \frac{125}{16}=\]
\[125\]
Letra D.
Pregunta n° 20

Solución: podemos calcular rápidamente día a día o bien utilizar una potencia, yo haré lo primero
- Día 1: (20)
- Día 2: (40)
- Día 3: (80)
- Día 4: (160)
- Día 5: (320)
- Día 6: (640)
- Día 7: (1.280)
- Día 8: (2.560)
- Día 9: (5.120)
- Día 10: (10.240)
Letra C.
Pregunta n° 21

Solución: Para resolver debemos reemplazar (n=10.000) y recordar que cuando sacamos la raíz cuadrada de una potencia de 10, es quitarle la mitad de los ceros (o pensar el número, como ustedes quieran :D).
\[0,001\cdot n \cdot \sqrt{n}=\]
\[0,001\cdot 10.000 \cdot \sqrt{10.000}=\]
\[0,001\cdot 10.000 \cdot 100=\]
\[\frac{1}{1000}\cdot 10.000 \cdot 100=\]
\[10 \cdot 100=\]
\[1000\]
Letra B.
Pregunta n° 22

Solución: Podemos entender la alternativa correcta al reemplazar \(m=0\) esto quiere decir cuando aún no ha pasado tiempo, es decir, el momento inicial.
\[k\cdot 2^0=\]
\[k\cdot 1=\]
\[k\]
entonces \(k\) es la cantidad inicial de archivos (\(2\) representa los archivos copiados, «el doble» y \(m\) las horas, es decir, la cantidad de veces que se ha duplicado).
Letra D.
Pregunta n° 23

Solución: Esta pregunta es muy simple, sólo debemos entender que debemos repartir el dinero total en el precio \(A\) de cada artículo.
\[\frac{350.000}{A}\]
Letra A.
Pregunta n° 24

Solución: Lo primero es plantear el sucesor de \(p\), es decir, \(p+1\) y ahora obtener su tercera parte
\[\frac{p+1}{3}\]
Letra D.
Pregunta n° 25

Solución: Para resolver, obtendremos primeramente la cantidad total de litros multiplicando la cantidad de contenedores por su capacidad y luego dividiremos este resultado en la capacidad de los nuevos contenedores
\[80\cdot 200=\]
\[16.000\]
esto es la cantidad total, ahora dividimos
\[16.000 : 50=\]
\[320\]
Letra C.
Pregunta n° 26

Solución: Para resolver podemos encontrar cuanto gasta en 1 día y multiplicarlo por 2 o bien darnos cuenta que la expresión representa lo gastado en 8 días por lo tanto para encontrar lo que gasta en 2, debemos dividir por 4 (o multiplicar por \(\frac{1}{4}\)).
\[\frac{1}{4}\cdot (a+1.600)=\]
\[\frac{1}{4}\cdot a + 400=\]
Letra A.
Pregunta n° 27
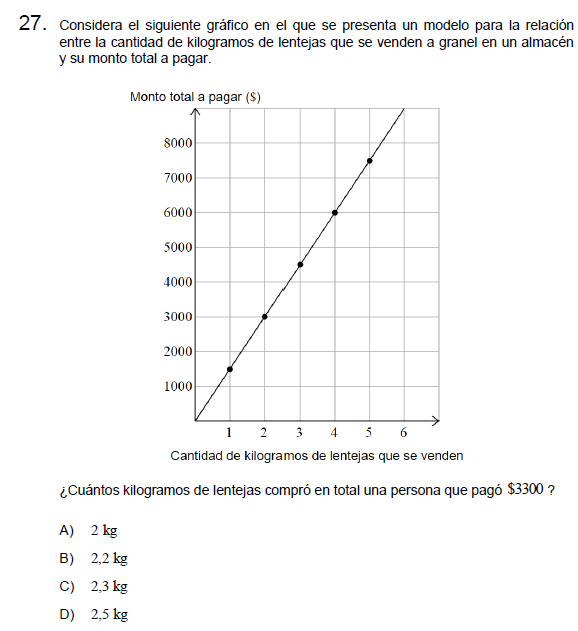
Solución: Para resolver podemos plantear una proporción identificando algún punto de la gráfica, por ejemplo, el punto (2,3000), entonces la proporción sería
\[\frac{kg}{precio}=\frac{2}{3.000}=\frac{x}{3.300}\]
\[\frac{2}{3.000}=\frac{x}{3.300}\]
\[\frac{2\cdot 3.300}{3.000}=x\]
\[\frac{6.600}{3.000}=x\]
\[\frac{66}{30}=x\]
\[\frac{6,6}{3}=x\]
\[2,2=x\]
Letra B.
Pregunta n° 28

Solución: Para esta pregunta plantearemos nuevamente una proporción.
\[\frac{km}{litros}=\frac{90}{15}=\frac{x}{25}\]
\[\frac{90}{15}=\frac{x}{25}\]
\[\frac{90\cdot 25}{15}=x\]
\[\frac{90\cdot 5}{3}=x\]
\[30\cdot 5=x\]
\[150=x\]
Letra D.
Pregunta n° 29

Solución: Para resolver me gusta plantear las razones como «partes de un total» en este caso el total corresponde a los 12.000 dólares, por lo cual, el primer lugar tiene 6 partes, el segundo 3, el tercero 2 y el último 1, debemos hallar a cuanto equivale 1 parte \((x)\) para poder calcular los montos.
\[12.000=6x+3x+2x+1x\]
\[12.000=12x\]
\[\frac{12.000}{12}=x\]
\[1.000=x\]
La persona en segundo lugar tiene 3 partes, es decir,
\[3\cdot 1.000=3.000\]
Letra B.
Pregunta n° 30

Solución: Para resolver debemos despejar la incógnita
\[\frac{2}{3}+x=\frac{3}{2}\]
\[x=\frac{3}{2}-\frac{2}{3}\]
\[x=\frac{9}{6}-\frac{4}{6}\]
\[x=\frac{5}{6}\]
Letra D.
Pregunta n° 31

Solución: Para resolver basta con identificar claramente los datos y reemplazar
- \(c=50\)
- \(L=30\)
\[L=c-0,1\cdot x\]
\[30=50-0,1\cdot x\]
\[0,1\cdot x+30=50\]
\[\frac{1}{10}\cdot x=50-30\]
\[\frac{1}{10}\cdot x=20\]
\[x=20\cdot 10\]
\[x=200\]
Letra C.
Pregunta n° 32

Solución: Para resolver podemos ir contando y sumando los gramos de cada capa, lo importante es respetar la condición dada
- Bizcocho (100g)
- Manjar (150g)
- Bizcocho (100g)
- Manjar (150g)
- Bizcocho (100g)
- Total 600g
Esta combinación respeta la condición dada y se ve que si añadimos una capa más superamos los 700 gramos, por lo tanto solamente podemos tener 2 capas de manjar.
Letra B.
Pregunta n° 33

Solución: Podemos resolver de varias maneras, probando alternativas, planteando las funciones y evaluando o bien la que propongo que es igualar ambas expresiones para saber que cantidad de invitados iguala los costos y con eso saber que 1 invitado más hace que sea más caro.
x será la cantidad de invitados
\[2000x+520.000=5000x+310.000\]
\[520.000=3000x+310.000\]
\[210.000=3000x\]
\[210=3x\]
\[70=x\]
Con 70 invitados se cobra lo mismo, por lo tanto, con 71 el segundo recinto (que cobra más por invitado) será más caro.
Letra B.
Pregunta n° 34

Solución: Para resolver es la propia alternativa quien da la explicación, las demás alternativas se pueden descartar solo poniendo atención a las condiciones del enunciado.
Letra A.
Pregunta n° 35

Solución: Para resolver este problema igualaremos ambas expresiones y despejaremos la «t»
\[\frac{4.000}{3}\cdot t + 4.000 = 2.000\cdot t\]
Multiplicaré todo por 3, para eliminar el denominador
\[4.000\cdot t + 12.000 = 6.000\cdot t\]
\[12.000 = 6.000\cdot t – 4.000\cdot t\]
\[12.000 = 2.000\cdot t\]
\[\frac{12.000}{2.000} = t\]
\[6 = t\]
Letra C.
Pregunta n° 36

Solución: Para resolver debemos reemplazar los datos otorgados y despejar la estatura (e).
\[masa=e^2 \cdot IMC\]
\[54=e^2 \cdot 24\]
\[\frac{54}{24}=e^2\]
simplificamos
\[\frac{9}{4}=e^2\]
\[\sqrt{\frac{9}{4}}=e\]
\[\frac{3}{2}=e\]
\[1,5=e\]
Letra C.
Pregunta n° 37

Solución: Para resolver este problema, debemos reemplazar el 1.000.000 en la fórmula y despejar la incógnita. También podríamos probar reemplazando los valores de las alternativas y ver cual cumple la condición.
\[U(x)=-\frac{1}{2}(x-12)^2+1.000.000\]
\[1.000.000=-\frac{1}{2}(x-12)^2+1.000.000\]
\[0=-\frac{1}{2}(x-12)^2\]
en este punto la pregunta a resolver es otra, ¿qué valor debe tener (x) para que la expresión valga 0?
lo cuál es 12, pues.
\[0=-\frac{1}{2}(x-12)^2\]
\[0=-\frac{1}{2}(12-12)^2\]
\[0=-\frac{1}{2}(0)^2\]
\[0=0\]
Letra B.
Pregunta n° 38
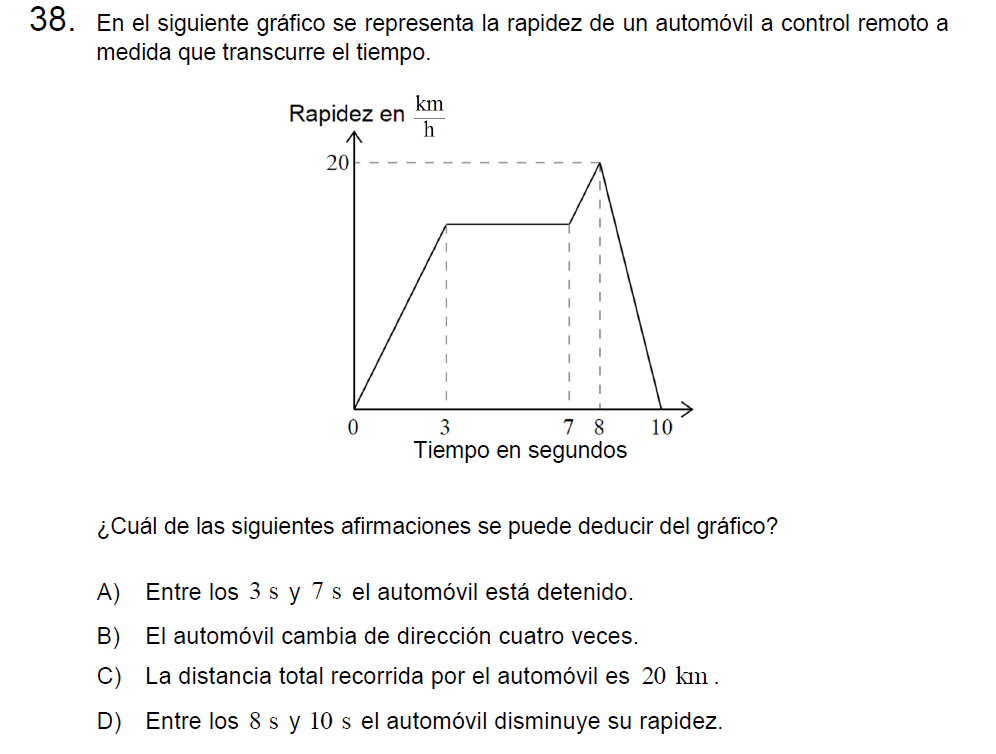
Solución: Para resolver iré respondiendo por qué no son correctas las alternativas y descartaremos hasta encontrar la correcta.
- A = entre este tiempo el automóvil mantiene una velocidad constante.
- B = no podemos saberlo ya que hablamos de cambio de rapidez y no de dirección, podría ser todo en una línea recta.
- C = esto no es correcto, podemos demostrarlo al decir que para recorrer esa distancia debería viajar durante 1 hora a la máxima rapidez que muestra el gráfico y solo tenemos 10 segundos.
- D = CORRECTA! es clara la disminución de rapidez en este tramo.
Letra D.
Pregunta n° 39

Solución: Para resolver esta pregunta es necesario probar 1 a 1 las alternativas.
- A = Nota = \(\frac{35}{14} + 2 = 4,5\)
- B = Nota = \(\frac{50}{14} + 2 = 5,57\)
- C = para que aumente en uno la nota debe aumentar 14 puntos.
- D = cuando se tienen 0 puntos \(\frac{0}{14}+2=2\), CORRECTA!
Letra D.
Pregunta n° 40

Solución: Para resolver debemos reemplazar los 3 s en la fórmula \(t\) y luego calcular.
\[f(t)=-(t)^2+2t+8\]
\[f(3)=-(3)^2+2(3)+8\]
\[f(3)=-9+6+8\]
\[f(3)=-9+14\]
\[f(3)= 5\]
Letra A.
Pregunta n° 41

Solución: Para resolver podemos utilizar el teorema de Pitágoras, la altura del árbol corresponde a la medida de un cateto, por lo que tenemos
\[12^2+ altura^2 = 15^2\]
\[144+ altura^2 = 225\]
\[altura^2 = 225-144\]
\[altura^2 = 81\]
\[altura= \sqrt{81}\]
\[altura= 9\]
Letra A.
Pregunta n° 42

Solución: Para resolver utilizando la fórmula, debemos encontrar primero la medida de la hipotenusa (c), una vez la tengamos reemplazamos todos los valores en la fórmula y despejamos. Finalmente para sacar el perímetro utilizamos el radio (mitad del diámetro) y la fórmula \(2\pi r\)
La hipotenusa la encontraremos usando Pitágoras
\[8^2+6^2=c^2\]
\[64+36=c^2\]
\[100=c^2\]
\[\sqrt{100}=c\]
\[10=c\]
Ahora reemplazamos en la fórmula inicial
\[8 + 6 = 10 + d\]
\[14 = 10 + d\]
\[4 = d\]
finalmente
\[P=2\pi \cdot 2\]
\[P=4\pi\]
Letra C.
Pregunta n° 43

Solución: Para resolver este problema utilizaremos el consejo que siempre doy a mis alumnos «Al área grande, reste el área chica», traducido sería, obtengamos el área del cuadrado y restémosle las áreas de los triángulos, en este caso, todos los triángulos son iguales, por lo que, sacando el área de 1, tendremos el área de los 4.
- Área cuadrado = \(p^2\)
- Área triángulo = \(\frac{m\cdot n}{2}\)
- Área total triángulos = \(4 \cdot \frac{m\cdot n}{2}= 2\cdot m \cdot n\)
- Área final = \(p^2 – 2\cdot m \cdot n\)
Letra D.
Pregunta n° 44

Solución: Para resolver debemos recordar la forma de calcular el volumen de un paralelepípedo (forma de caja) y como digo a mis alumnos: «la mayoría de las veces el volumen se calcula como el área de la base por la altura.
Las nuevas medidas serían 10 y 16
- Área base = \(10^2=100\)
- Volumen = \(100 \cdot 16=1.600\)
Letra C.
Pregunta n° 45

Solución: Para resolver debemos obtener el volumen de los bloques de vidrio, por lo tanto, obtendremos el volumen de 1 y multiplicaremos por 10 (son diez bloques).
El volumen será igual al área de la base por la altura.
\[V=20^2\cdot 8\]
\[V=400\cdot 8\]
\[V=3200\]
ahora multiplicamos por 10
\[V_{final}=3200\cdot 10\]
\[V_{final}=32000\]
Letra C.
Pregunta n° 46

Solución: Para resolver este problema tendremos que escribir el volumen de la esfera M en términos de R y \(\pi\). Primero despejaremos R y posteriormente lo reemplazaremos en la fórmula del volumen del cono.
\[M=\frac{4\pi R^3}{3}\]
\[3M=4\pi R^3\]
\[\frac{3M}{4\pi}=R^3\]
\[\sqrt[3]{\frac{3M}{4\pi}}=R\]
lo tenemos despejado ahora lo reemplazamos en la fórmula del cono, afortunadamente tanto el radio como la altura del cono son iguales.
\[V=\frac{\pi r^2 h}{3}\]
\[V=\frac{\pi (\sqrt[3]{\frac{3M}{4\pi}})^2 \cdot \sqrt[3]{\frac{3M}{4\pi}}}{3}\]
tenemos multiplicación de potencias de igual base por lo que nos queda
\[V=\frac{\pi (\sqrt[3]{\frac{3M}{4\pi}})^3}{3}\]
\[V=\frac{\pi \cdot \frac{3M}{4\pi}}{3}\]
\[V=\frac{\frac{3M}{4}}{3}\]
\[V=\frac{M}{4}\]
Letra A.
Pregunta n° 47

Solución: Para resolver este problema puede resultar de mucha ayuda dibujar el plano cartesiano y ubicar los puntos. Sin embargo, podemos pensar en lo siguiente:
Si es un punto en común a todos (queda en el centro) y los lados de los cuadrados miden 2 unidades, las coordenadas de los otros vértices se pueden obtener al sumarle 2 unidades en todas las direcciones.
- \((2,-3)+(2,2)=(4,-1)\)
- \((2,-3)+(-2,2)=(0,-1)\)
- \((2,-3)+(2,-2)=(4,-5)\)
La última corresponde a la alternativa.
Letra B.
Pregunta n° 48

Solución: Para resolver debemos pensar en el proceso inverso al realizado. Debemos rotar la figura y luego desplazarla hacia arriba y a la izquierda (Norte y Oeste) en las mismas cantidades. Es importante notar que en el proceso inicial se rota dos veces en 90° en el mismo sentido, lo cual equivale a una rotación de 180°.
Letra A.
Pregunta n° 49

Solución: Para resolver este problema, les comparto una imagen que he tomado de un material de Cpech acerca de las rotaciones en el plano respecto del origen, recuerden además que las rotaciones positivas son en sentido antihorario.
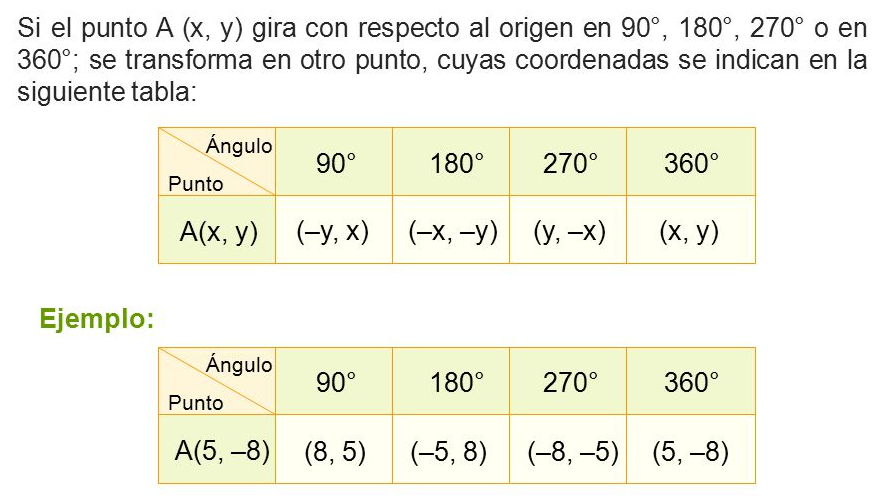
Con esta ayuda analicemos la pregunta.
- Al aplicar una reflexión en torno al eje Y lo único que cambia es el signo de la coordenada x (paso 1 correcto)
- La traslación realizada es correcta (se ha sumado los valores coordenada a coordenada)
- El paso 3 es incorrecto, pueden revisar la tabla y ver que debería quedar \((-y,x)\), es decir, \((-12,1)\)
Letra C.
Pregunta n° 50

Solución: Claramente es la letra M! 😀
Letra B.
Pregunta n° 51

Solución: Para resolver este problema, asumiremos que el centro del tablero corresponde al origen del plano (0,0), a estas coordenadas iremos sumando o restando según corresponda por las fichas.
\[(0,0)+(-3,1)+(2,-3)+(-1,-3)=\]
sumamos coordenada a coordenada (x con x, y con y)
\[(0-3+2-1, 0+1-3-3)=\]
\[(-2,-5)\]
para volver al origen necesitamos los valores contrarios
\[(2,5)\]
es decir, 5 norte y 2 este.
Letra A.
Pregunta n° 52

Solución: Para resolver plantearemos una proporción que involucre las Medidas en el plano (MP) y las medidas en la realidad (MR).
\[\frac{MP}{1}=\frac{MR}{100}\]
\[MP=\frac{MR\cdot 1}{100}\]
\[MP=\frac{MR}{100}\]
Letra D.
Pregunta n° 53

Solución: Para resolver este problema, plantearemos una proporción y luego transformaremos las unidades de medida, pasando de mm a cm (se divide por 10).
\[\frac{realidad}{plano}=\frac{8}{1}=\frac{x}{95}\]
\[\frac{8}{1}=\frac{x}{95}\]
\[\frac{8\cdot 95}{1}=x\]
\[760=x\]
ahora dividimos por 10 y convertimos los mm a cm
\[760:10=x\]
\[76=x\]
Letra C.
Pregunta n° 54

Solución: Para resolver utilizaremos la semejanza de triángulos (se forma con el alto y la sombra), es decir, planteamos una proporción.
\[\frac{sombra}{alto}=\frac{3}{4}=\frac{12}{x}\]
Letra A.
Pregunta n° 55
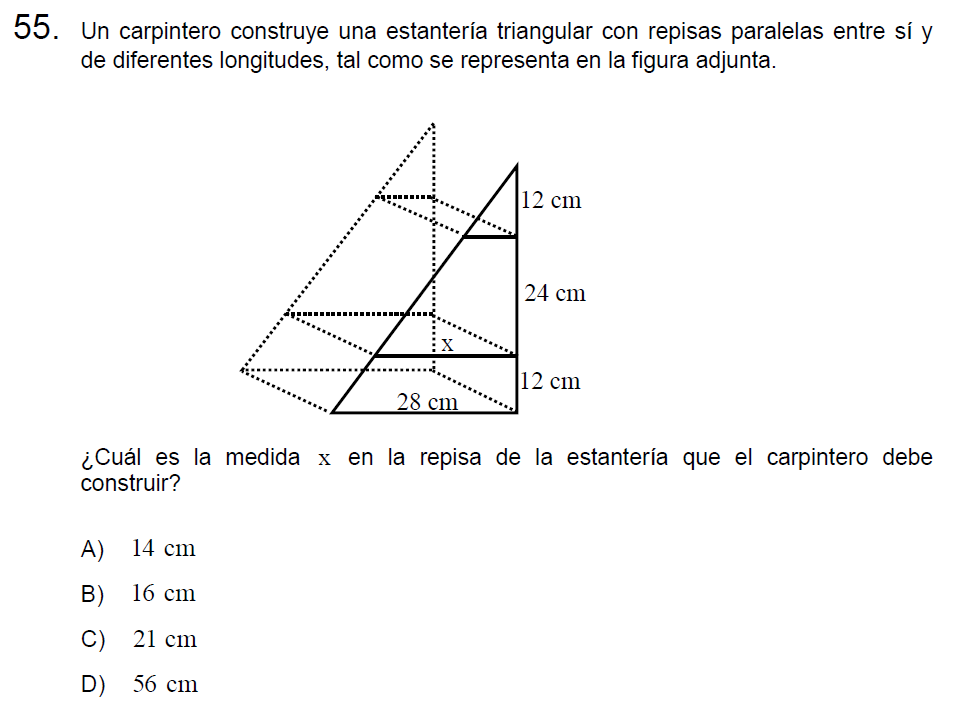
Solución: Para resolver utilizaremos nuevamente la semejanza de triángulos (esto es posible porque las repisas son paralelas) entre el triángulo mediano y el triángulo grande.
Llamaremos base y altura a los lados de los triángulos, planteamos la proporción
\[\frac{base}{altura}=\frac{x}{12+24}=\frac{28}{12+24+12}\]
\[\frac{x}{36}=\frac{28}{48}\]
\[x=\frac{28\cdot 36}{48}\]
\[x=\frac{28\cdot 3}{4}\]
\[x=7\cdot 3\]
\[x=21\]
Letra C.
Pregunta n° 56
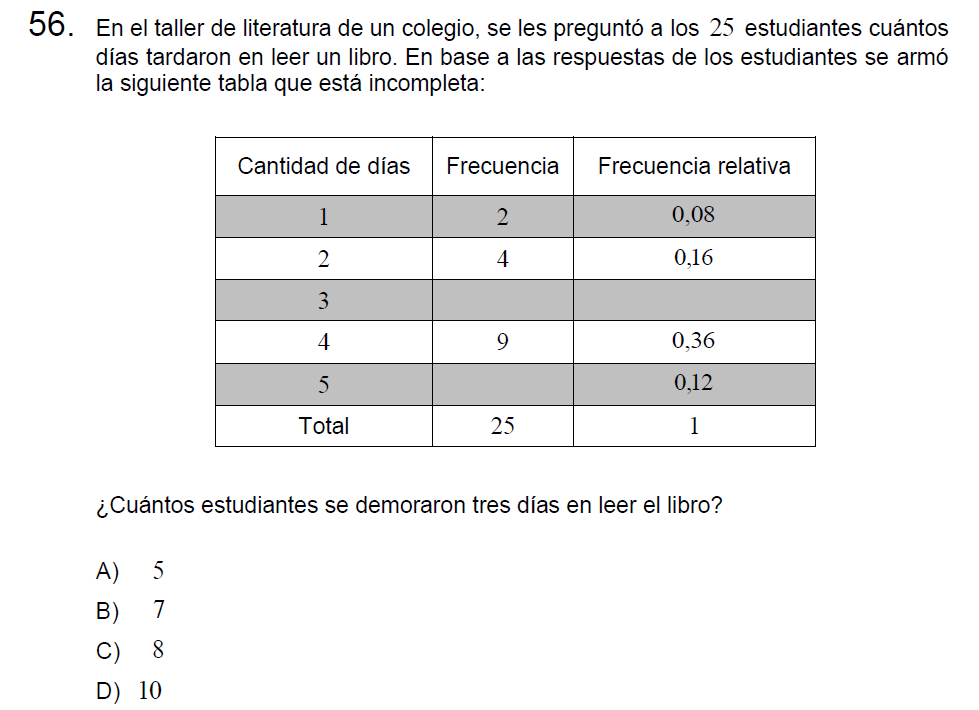
Solución: Para resolver completaremos en primer lugar la frecuencia relativa, para ello pensamos en cuanto nos falta para llegar a 1 o bien sumamos todas las frecuencias relativas y las restamos de 1.
\[0,08+0,16+x+0,36+0,12=1\]
\[x+0,72=1\]
\[x=1-0,72\]
\[x=0,28\]
ahora completamos la frecuencia (absoluta), para ello podemos multiplicar su respectiva frecuencia relativa del total de datos (25).
\[0,28\cdot 25=\]
\[\frac{28\cdot 25}{100}=\]
\[\frac{700}{100}=\]
\[7\]
yo multiplico así ustedes pueden hacerlo como gusten 🤓 .
Letra B.
Pregunta n° 57

Solución: Para resolver solo debemos sumar las frecuencias.
\[6+3+2+3+1=\]
\[15\]
Letra C.
Pregunta n° 58

Solución: Para resolver este problema, podemos hacerlo de dos formas distintas:
- Multiplicar todas las notas por el factor y luego sacar el promedio.
- Sacar el promedio y luego multiplicarlo por el factor.
Yo haré el segundo método
\[\bar{x}=\frac{5+4+4+3+4}{5}\]
\[\bar{x}=\frac{20}{5}\]
\[\bar{x}=4\]
ahora multiplicamos por el factor
\[\bar{x}=\frac{6}{5}\cdot 4\]
\[\bar{x}=\frac{24}{5}\]
\[\bar{x}=4,8\]
los invito a que realicen el otro procedimiento y verifiquen si da el mismo resultado 😉 .
Letra B.
Pregunta n° 59
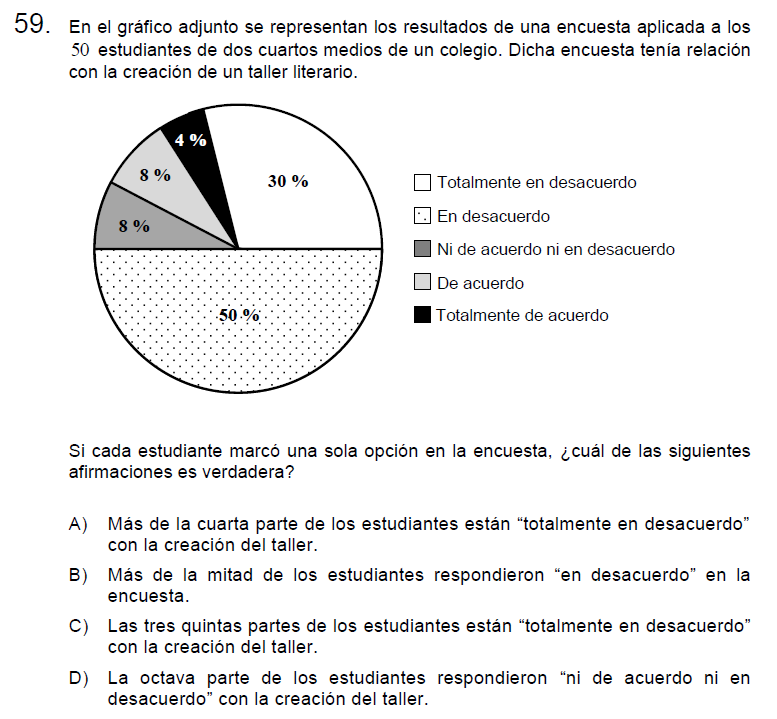
Solución: Para resolver iremos comprobando las alternativas una por una.
- A: la cuarta parte de algo, significa obtener su 25% por lo cual es correcto afirmar que más de la cuarta parte de los estudiantes están «totalmente en desacuerdo».
con esto ya tenemos la alternativa correcta, sin embargo, les dejaré las equivalencias de las otras alternativas.
- B: la mitad equivale al 50%
- C: las tres quintas partes equivale al 60%
- D: la octava parte corresponde al 12,5%
Letra A.
Pregunta n° 60

Solución: Para resolver esta pregunta basta con contar,
- Adolescentes de 12 años: 4
- Adolescentes de 13 años: 10
- Adolescentes de 14 años: 18
- Adolescentes de 15 años: 5
Letra C.
nota: no soy muy bueno contando, así que si se me pasó alguno me avisan por favor 😔.
Pregunta n° 61
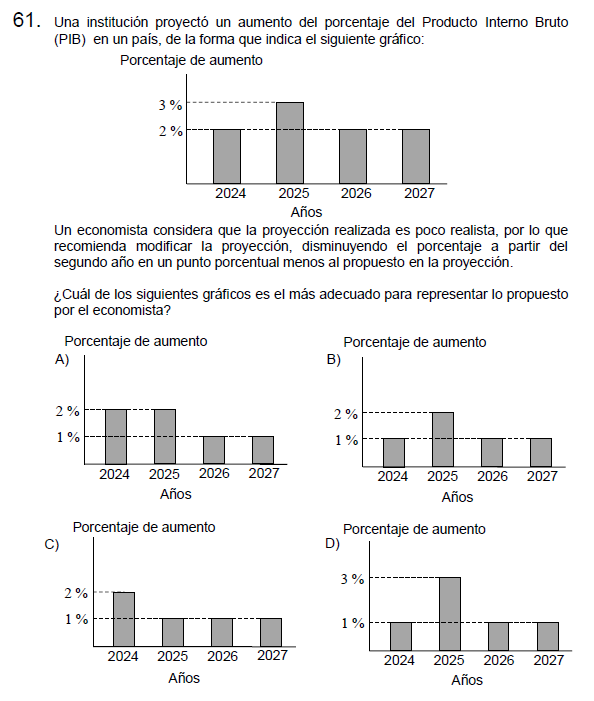
Solución: Para resolver este problema debemos observar desde el año 2025 en adelante, cada una de esas barras bajará 1 punto, por lo que quedarán en 2%, 1% y 1%.
Letra A.
Pregunta n° 62

Solución: Para responder esta pregunta debemos recordar qué medida de posición agrupa de a 25%.
Los cuartiles, son tres y cada uno de ellos separa los datos en grupos de 25%, por lo tanto el cuartil 1 agrupa el 25% el cuartil 2 el 50% y el cuartil 3 marca el 75% de los datos.
Los percentiles por su parte son 99 y dividen la totalidad de los datos en 100 partes cada una de un 1%, por ejemplo, el percentil 4 marca el 4% de los datos.
Letra D.
Pregunta n° 63

Solución: Para resolver calcularemos la probabilidad usando la regla de Laplace, para ello necesitamos el total de los números, esto lo hallaremos multiplicando las 100 listas por los 20 números que tiene cada una.
\[100\cdot 20 = 2000\]
ahora usamos la regla de Laplace
\[\frac{casos favorables}{casos totales}=\frac{8}{2000}\]
Letra D.
Pregunta n° 64

Solución: Para resolver iremos sacando la información desde el enunciado
- Leer = 30
- Deporte = 48
- Películas = n
Con la información dada, si la probabilidad de que el pasatiempo de una persona no sea hacer deporte sea de 0,6, se tiene que
\[\frac{Leer+Películas}{Leer + películas + Deporte}=0,6\]
\[\frac{30+n}{30 + n + 48}=0,6\]
\[\frac{30+n}{78 + n}=\frac{6}{10}\]
\[10\cdot (30+n)=6\cdot (78 + n)\]
\[300+10n=468 + 6n\]
\[4n=168\]
\[n=42\]
Letra B.
Pregunta n° 65

Solución: Para resolver debemos verificar paso a paso
- Paso 1: todas las combinaciones están bien, son 8 en total.
- Paso 2: la elección de los casos está bien.
- Paso 3: el cálculo de las probabilidades está INCORRECTO, ya que para cada una es solo 1 caso favorable de un total de 8, debiera ser \(\frac{1}{8}\).
Letra C.
