Hola a tod@s!, les traigo una breve entrada relacionada a desigualdades e inecuaciones, este contenido no es muy extenso (lo que aparece en la PAES), por lo que veremos lo básico para que puedan defenderse en la escuela.
Desigualdades: ¿Qué son y qué propiedades tienen?
Definiciones
Vamos a traducir estos conceptos, cuando hablamos de desigualdad nos referimos a una comparación entre dos cantidades, solemos escribir algo como:
- \(a>b\) Se lee «a» es mayor que «b», esto quiere decir además que \(a-b\) es positivo (mayor que 0)
- \(a<b\) Se lee «a» es menor que «b», esto quiere decir además que \(a-b\) es negativo (menor que 0)
Los símbolos que vamos a utilizar son \(>,<, \geq, \leq\), mayor, menor, mayor o igual, menor o igual, respectivamente.
Propiedades
Si a los dos miembros (lados) de una desigualdad se suma (o resta) un mismo número, el sentido de la desigualdad NO cambia. Esto lo escribimos mediante símbolos de la siguiente manera:
Si \(a,b,c\) son números reales y \(a<b\), entonces
\[a+c<b+c\]
Si los dos miembros (lados) de una desigualdad se multiplican por un mismo número positivo, el sentido de la desigualdad NO cambia. Esto lo escribimos mediante símbolos de la siguiente manera:
Si \(a,b,c\) son números reales tales que \(a<b, c>0\), entonces
\[ac<bc\]
Si los dos miembros (lados) de una desigualdad se multiplican por un mismo número negativo, el sentido de la desigualdad SÍ cambia. Esto lo escribimos mediante símbolos de la siguiente manera:
Si \(a,b,c\) son números reales tales que \(a<b, c<0\), entonces
\[ac>bc\]
Si de los dos miembros de una desigualdad, se toman inversos multiplicativos (recíprocos), el sentido de la desigualdad cambia.
Si los dos miembros de una desigualdad son positivos y se elevan a la misma potencia, la desigualdad NO cambia de sentido.
Si los dos miembros de una desigualdad son negativos y se elevan a una potencia de grado impar, NO cambia el sentido de la desigualdad; sin embargo, si el grado de la potencia es par, SÍ cambia de sentido.
Ejemplos:
1. Sean \(a\) y \(b\) números enteros negativos, ¿cuál(es) de las siguientes desigualdades es (son) VERDADERA(s)?
I. \(-a-b>0\)
II. \((a+b)^3<0\)
III. \(-b<b\)
Solución:
Probaremos una a una
I. Si \(a\) y \(b\) son negativos, sus inversos aditivos (\(-a, -b\)) son positivos. Por lo tanto, si les otorgamos valores tenemos una situación como
\[-(-2)-(-3)>0\]
\[2+3>0\]
Lo cual es verdadero.
II. Si sumamos dos números negativos, el resultado es negativo y luego si lo elevamos a una potencia impar, nuevamente será negativo, veamos un caso puntual
\[(-2+(-3))^3<0\]
\[(-5)^3<0\]
\[-125<0\]
Lo cual es verdadero.
III. El inverso aditivo de \(b\) es positivo por lo cual esta opción es falsa ya que nos dicen que un número positivo es menor que un negativo. Veamos un caso puntual
\[-(-2)<-2\]
\[2<-2\]
Lo correcto sería I y II.
2. Para que la expresión \(\frac{1-\frac{x+y}{x-y}}{1+\frac{x+y}{x-y}}\) sea positiva, se debe cumplir necesariamente que:
Solución:
Para que la expresión sea positiva, tanto numerador como denominador deben tener el mismo signo.
Primero vamos a organizar la expresión:
\[\frac{1-\frac{x+y}{x-y}}{1+\frac{x+y}{x-y}}\]
Transformaré el 1
\[=\frac{\frac{x-y}{x-y}-\frac{x+y}{x-y}}{\frac{x-y}{x-y}+\frac{x+y}{x-y}}\]
\[=\frac{\frac{x-y-(x+y)}{x-y}}{\frac{x-y+x+y}{x-y}}\]
\[=\frac{\frac{-2y}{x-y}}{\frac{2x}{x-y}}\]
\[=\frac{-2y}{x-y}\cdot \frac{x-y}{2x}\]
\[=\frac{-y}{x}\]
Con esto mucho más simplificado podemos analizar, si ambos deben tener el mismo signo implica que
El signo de \(x\) debe ser igual al signo de \(-y\), esto implica que el signo de \(x\) es contrario al signo de \(y\) y por lo tanto \(x\cdot y < 0 \)
Inecuaciones: ¿qué son y cómo se resuelven?
En palabras sencillas podríamos decir que nos referimos a desigualdades donde existe una incógnita a descubrir. La gran diferencia con las ecuaciones radica en que, las posibles respuestas pueden ser, un valor, ningún valor, un conjunto de valores, infinitos valores!.
Para resolverlas debemos despejar la incógnita x, teniendo en cuenta las propiedades de las desigualdades. Al igual que con las ecuaciones podemos sumar, restar, multiplicar, dividir en ambos lados de la inecuación, solo recuerda que si lo haces por un número negativo debes invertir el sentido del símbolo.
Ejemplos de inecuaciones resueltas:
1. ¿Cuál es el conjunto solución de la inecuación \(2x+7\leq 12+x\)?
Solución:
\[2x+7\leq 12+x\]
\[2x-x\leq 12-7\]
\[x\leq 5\]
\[S=]^-\infty,5]\]
2. La inecuación \(\frac{1}{2}(8-2x)<-7\) tiene como conjunto solución:
Solución:
\[\frac{1}{2}(8-2x)<-7\]
\[4-x<-7\]
\[-x<-11\]
Multiplicamos por \(-1\), recordando invertir el signo
\[x>11\]
\[S=]11,\infty[\]
Inecuaciones de segundo grado: ¿qué son y cómo se resuelven?
Guardan mucha semejanza con las ecuaciones de segundo grado (cuadráticas), tendremos expresiones de la forma:
\[ax^2+bx+c\leq 0\]
El proceso de resolución que puedo sugerirles es:
- Se debe dejar cero a un lado de la igualdad (cambiando de lado las expresiones).
- Factorizar la expresión.
- Encontrar los puntos críticos de la ecuación (valores que hacen cero cada factor o indeterminan la expresión).
- Construir una tabla donde se incorporen los valores críticos y se analicen lo signos resultantes.
- Analizar para cada rango, si el producto de los factores será + o -.
- Construir el conjunto solución con los intervalos que cumplen con la condición inicial (mayor o menor que 0)
Ejemplos:
1. \(x^2+5x-6>0\)
Solución:
En primer lugar factorizamos la expresión
\[(x+6)(x-1)>0\]
Los puntos críticos son \(-6\) y \(1\), con estos valores construimos la tabla:

Con la tabla construida, buscamos los intervalos que nos sirvan, lo solicitado es «mayor que 0 (>0)» por lo tanto buscamos los intervalos con signos +.
\[S=]^-\infty,-6[\cup ]1,\infty^+[\]
2. \(\frac{x^2+x-2}{x+3}\leq 0\)
Solución:
Factorizamos el numerador para obtener todos los puntos críticos
\[\frac{x^2+x-2}{x+3}\leq 0\]
\[\frac{(x+2)(x-1)}{x+3}\leq 0\]
Los puntos críticos serían -3, -2 y 1. (El -3 porque aquí se indetermina la fracción ya que el denominador queda en 0)
Con esto construimos la tabla

Nos centramos en lo solicitado (Menor o igual a 0, \(\leq 0)\)
\[S=]^-\infty,-3[\cup [-2,1]\]
Sistemas de inecuaciones lineales con una incógnita: ¿qué son y cómo se resuelven?
Esto es un sistema formado por dos o más inecuaciones de primer grado con una incógnita.
El conjunto solución del sistema es la intersección de los conjuntos de cada inecuación. Es decir, se deben cumplir ambas condiciones al mismo tiempo.
Gráficamente correspondería a la intersección (donde se cruzan) de las soluciones.
Ejemplos:
\[x-1<2\]
\[x+1>2\]
Solución:
Resolvemos cada una por separado y posteriormente interceptamos los conjuntos solución.
\[x-1<2\]
\[x<3\]
\[S=]^-\infty,3[\]
\[x+1>2\]
\[x>1\]
\[S=]1,\infty^+[\]
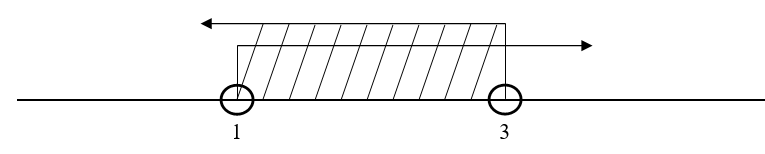
Finalmente la solución es
\[S=]1,3[\]
Problemas de inecuaciones resueltos
En estos problemas aparecen expresiones que hay que traducir a los símbolos \(>, <, \geq o \leq\), tales como:
- a lo menos (\(\geq\))
- cuando mucho (\(\leq\))
- como mínimo (\(\geq\))
- como máximo (\(\leq\))
- sobrepasa (\(>\))
- no alcanza (\(<\))
Una vez planteada la inecuación o sistema de inecuaciones, se determina el conjunto solución, y al igual que en los problemas de ecuaciones hay que fijarse en la pegunta del problema.
Ejemplos:
1. Si 7 veces un número disminuye en 5 unidades resulta un número menor que 47, entonces el número debe ser menor que
a. 42 b. 49 c. 52 d. \(\frac{82}{7}\) e. \(\frac{52}{7}\)
Solución:
Traducimos el «un número» como X y completamos con las operaciones que nos describen
\[7x-5<47\]
\[7x<52\]
\[x<\frac{52}{7}\]
2. «El triple del sucesor de un número entero x no es menor ni igual que el doble del cuadrado del doble de x», es equivalente a
Solución:
Vamos paso a paso, el sucesor de un número entero se representa como
\[x+1\]
El triple de lo anterior sería
\[3(x+1)\]
la frase «no es menor ni igual» significa «es mayor», hasta aquí llevamos
\[3(x+1)>\]
Nos queda por traducir «el doble del cuadrado del doble de x», esto lo haremos iniciando desde atrás
el doble de x
\[2x\]
el cuadrado de \(2x\)
\[(2x)^2\]
El doble de lo anterior
\[2(2x)^2\]
Uniendo todo nos queda
\[3(x+1)>2(2x)^2\]
Inecuaciones con valor absoluto
¿Qué es el valor absoluto?
El valor absoluto de un número \(a\), denotado como \(|a|\), es la distancia desde \(a\) hasta el cero en la recta numérica. Por lo tanto:
\[|a| = \begin{cases} a & \text{si } a \geq 0, \\ -a & \text{si } a < 0. \end{cases}\]
Tipos de inecuaciones con valor absoluto
Existen varios tipos comunes de inecuaciones con valor absoluto:
1. Inecuaciones de la forma \(∣x∣<c\)
- \(c\) debe ser un número positivo, \(c>0\).
- Se convierte en una doble desigualdad: \( ∣x∣<c ⇒−c<x<c\). Esto significa que \(x\) está dentro del intervalo \((−c,c)\).
Ejemplo: Resolver \(∣x∣<4\)
\[∣x∣<4⇒−4<x<4\]
Solución: \(x∈(−4,4)\).
2. Inecuaciones de la forma \(∣x∣>c\)
- \(c\) debe ser un número positivo, \(c>0\).
- Se convierte en dos desigualdades: \(∣x∣>c⇒x<−c o x>c\). Esto significa que \(x\) está fuera del intervalo (−c,c).
Ejemplo: Resolver \(∣x∣>3\)
\[∣x∣>3⇒x<−3 o x>3\]
Solución: \(x \in (-\infty, -3) \cup (3, \infty)\).
3. Inecuaciones más generales \(∣ax+b∣<c\)
- Se resuelven reescribiendo como una doble desigualdad: \(−c<ax+b<c\).
- Luego se resuelve despejando \(x\).
Ejemplo: Resolver \(∣2x−1∣<5\)
\[−5<2x−1<5\]
Sumamos 1 a todos los miembros de la inecuación:
\[−4<2x<6\]
Dividimos entre 2
\[−2<x<3\]
Solución: \(x \in (-2, 3)\).
Inecuaciones con doble valor absoluto
Resolver inecuaciones con doble valor absoluto puede ser un poco más complicado que las inecuaciones simples, pero el proceso es manejable si seguimos un enfoque paso a paso. Vamos a verlo con un ejemplo:
Ejemplo:
Resolver la inecuación: \(∣x−3∣+∣2x+1∣<5\)
Paso 1: Identificar los puntos críticos
Los valores críticos son los que hacen que el contenido de los valores absolutos sea igual a 0, es decir, para determinarlos debemos resolver una pequeña ecuación con el contenido de cada valor absoluto. Para \(|x – 3|\), el punto crítico es \(x=3\) y para \(|2x + 1|\), el punto crítico es \(x=-\frac{1}{2}\).
Estos puntos dividen el dominio en intervalos donde cada expresión dentro de los valores absolutos tiene un signo definido.
Paso 2: Dividir en intervalos
Los puntos críticos \(x=-\frac{1}{2}\) y \(x=3\) dividen el eje real en tres intervalos:
- \(x < -\frac{1}{2}\)
- \(-\frac{1}{2} \leq x < 3\)
- \(x \geq 3\)
Paso 3: Resolver en cada intervalo
Dentro de cada intervalo, eliminamos los valores absolutos asignando signos correctos a las expresiones.
Para \(x < -\frac{1}{2}\), el resultado dentro de ambos valores absolutos sería negativo:
- \(∣x−3∣=−(x−3)=−x+3\)
- \(∣2x+1∣=−(2x+1)=−2x−1\).
- La inecuación se convierte en:
\[−x+3−2x−1<5 \]
\[−3x+2<5\]
\[−3x<3\]
\[ x>−1\]
En este intervalo consideramos \(x < -\frac{1}{2}\) y como obtuvimos \(x > -1\), la solución válida es:
\[−1<x<−\frac{1}{2}\]
Para \(-\frac{1}{2} \leq x < 3\)
- \(∣x−3∣=−(x−3)=−x+3\)
- \(∣2x+1∣=2x+1\)
- La inecuación se convierte en:
\[ x+4<5\]
\[x<1\]
En este intervalo, tomamos \(-\frac{1}{2} \leq x < 3\) y \(x < 1\), por lo que la solución es \(-\frac{1}{2} \leq x < 1\).
Para \(x \geq 3\)
- \(|x – 3| = x – 3\)
- \(|2x + 1| = 2x + 1\)
- La inecuación se convierte en:
\[ 3x−2<5\]
\[3x<7\]
\[x < \frac{7}{3}\]
En este intervalo, tomamos \(x \geq 3\) y \(x < \frac{7}{3}\), por lo que no hay solución válida.
Paso 4: Unir las soluciones
Unimos las soluciones válidas de los intervalos:
- Del intervalo 1: \(-1 < x < -\frac{1}{2}\)
- Del intervalo 2: \(-\frac{1}{2} \leq x < 1\)
Por lo tanto, la solución final es:
\[x \in (-1, 1)\]
Conclusión:
El método general consiste en:
- Encontrar los puntos críticos.
- Dividir el dominio en intervalos según esos puntos.
- Resolver la inecuación en cada intervalo eliminando los valores absolutos.
- Combinar las soluciones válidas.
Espero que les sea útil, por su puesto, existen muchos más tipos de ejercicios, pero esto es lo básico que les servirá para defenderse ante los problemas :D.

Pingback: Resolución PAES m1 verano 2023 – Mates pal Colegio