Buenas a todos y todas, les traigo la resolución de la PAES M1 más reciente!
Esta versión va especialmente dedicada a mis estudiantes del 4B que rinden la PAES este año, mucho éxito! y cariños de su profe Esteban!
P1

Solución:
\[5-(-2)(-2-7)=\]
\[5-(-2)(-9)=\]
\[5-(18)=\]
\[-13\]
Letra B.
P2

Solución:
Podemos enumerarlos, 1 y 2, por lo tanto son solo 2
Letra A.
P3

Solución:
\[(\frac{3}{8}:-\frac{6}{16})-\frac{8}{3}=\]
\[(\frac{3}{8}\cdot-\frac{16}{6})-\frac{8}{3}=\]
\[(\frac{1}{1}\cdot-\frac{2}{2})-\frac{8}{3}=\]
\[-1-\frac{8}{3}=\]
\[-\frac{3}{3}-\frac{8}{3}=\]
\[-\frac{11}{3}\]
Letra A.
P4

Solución:
Para resolver debemos traducir el enunciado en una inecuación
\[\frac{11}{6}\cdot \frac{2}{3}<\frac{11}{6}\]
\[\frac{2}{3}<\frac{11}{6}\cdot \frac{6}{11}\]
\[\frac{2}{3}<1\]
Letra B.
P5

Solución:
Quienes llegaron después son aquellos que tardaron más minutos, siendo Mario el número más grande, ninguno de los otros pudo llegar después, él fue el último.
Letra D.
P6

Solución:
Teníamos 5 bolitas, y se nos asegura que todos los agujeros fueron utilizados, es decir, llevamos acumulados \(3 + 1 + 5 = 9\) puntos, nos quedan dos bolitas más, el máximo puntaje obtenido vendría de acertar estos últimos lanzamientos en el puntaje más alto, es decir, \(9 + 5 + 5 = 19\)
Letra C.
P7

Solución:
La variación de la temperatura corresponde a la diferencia entre ambas temperaturas, siendo la temperatura final menos la inicial, es decir,
\[24 – 29 =-5\]
Letra B.
P8
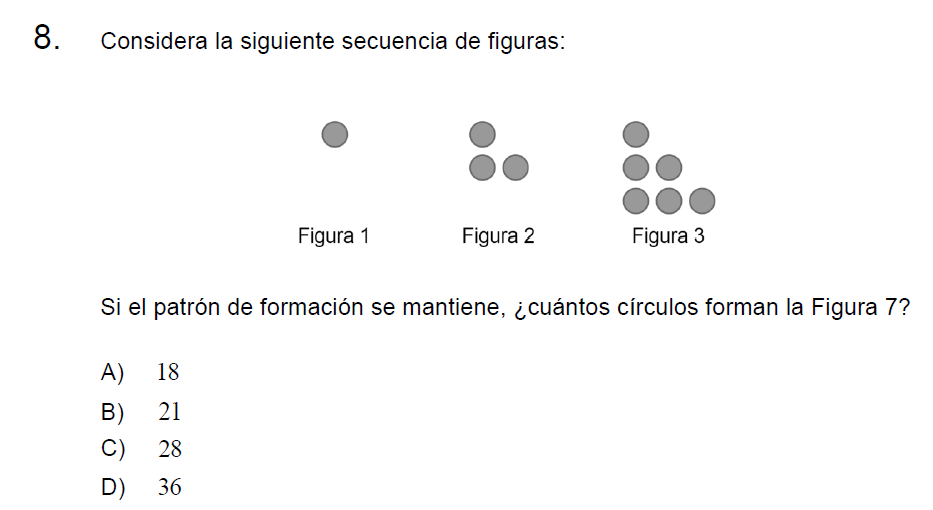
Solución:
La secuencia numérica es:
\[1 – 3 – 6\]
Cada fila que se añade, incorpora un círculo más, la figura 4 tendrá cuatro círculos más y así:
\[\text{figura 4}=6+4 = 10\]
\[\text{figura 5}=10+5 = 15\]
\[\text{figura 6}=15+6 = 21\]
\[\text{figura 7}=21+7 = 28\]
Letra C.
P9
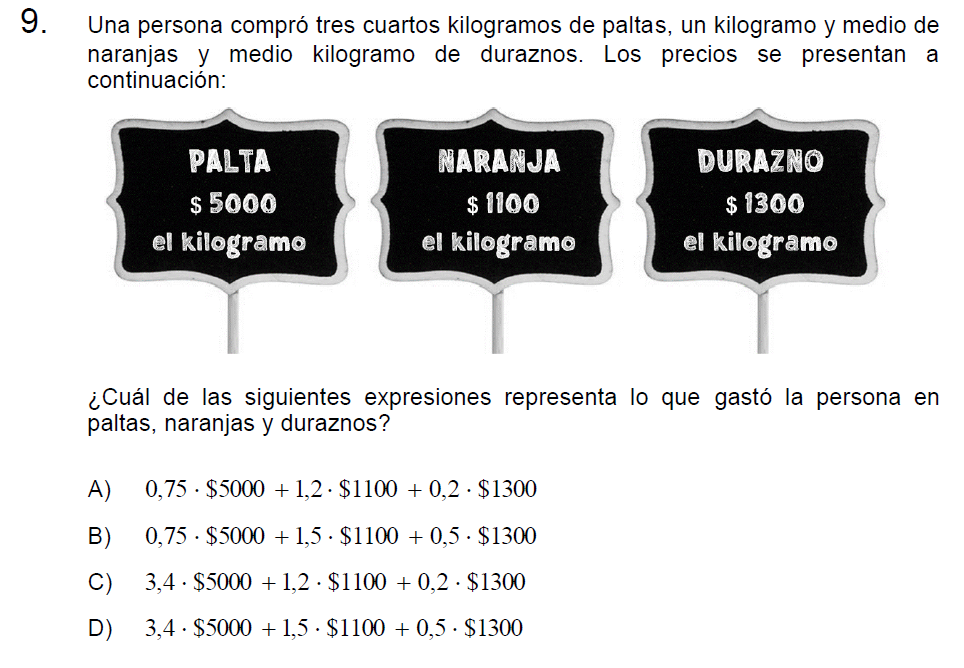
Solución:
Para resolver basta con saber transformar fracciones a decimales:
\[\text{tres cuartos} = \frac{3}{4}\to 3:4=0,75\]
\[\text{un kilogramo y medio} = 1\frac{1}{2}=\frac{3}{2}\to 3:2=1,5\]
\[\text{un medio} = \frac{1}{2}=\to 1:2=0,5\]
Letra B.
P10

Solución:
Lo primero es determinar cuántas libras de carne tenemos, como son dos trozos de un cuarto cada uno, tenemos 2 cuartos, es decir, media libra.
Ahora calculamos la mitad de una libra, es decir \(453,6 : 2\)
\[453,6 : 2=\]
\[226,8\]
Letra C.
P11

Solución:
Para resolver se debe tener claro, quién es la incógnita según los datos que nos entregan, nos piden encontrar los kilómetros, por lo cuál esta es la incógnita, por lo tanto, reemplazamos las dos millas en la «x».
\[C=160.934\cdot 2\]
\[C=321.868\]
Ahora dividimos esta cantidad de centímetros por 100.000, de esta manera los transformamos en kilómetros. Dividir por esta cantidad es tan sencillo como correr la coma 5 espacios quedando:
\[321.868:100.000=3,21868\]
Letra C.
P12

Solución:
Resolveré este ejercicio multiplicando 60 mil por \(\frac{15}{100}\)
\[60.000\cdot \frac{15}{100}=\]
\[600\cdot 15=\]
\[9000\]
Letra D.
P13

Solución:
Obtendremos este porcentaje utilizando una proporción añadiendo el 5%, es decir, obtendremos el 105%.
\[\frac{20}{100}=\frac{x}{105}\]
\[\frac{2}{10}=\frac{x}{105}\]
\[\frac{1}{5}=\frac{x}{105}\]
\[\frac{105}{5}=x\]
\[21=x\]
Letra A.
P14

Solución:
Veamos una por una,
A. Esto es INCORRECTO ya que ese porcentaje no es del planeta sino del agua dulce.
B. CORRECTA
C. Esto es INCORRECTO ya que esos números eran en relación a %, al eliminar ese símbolo debemos dividir nuevamente por 100.
D. Esto es INCORRECTO ya que hay muchísima más agua salada que dulce.
Letra B.
P15

Solución:
Para resolver debemos restar los puntos porcentuales \(32,1%-18,1%\)
\[32,1-18,1=14,0\]
Letra A.
P16

Solución:
Lo importante para resolver es determinar cuál es nuestro punto de inicio, ya que esto marcará al 100% en la proporción. En este caso será el año 2021 con sus 110.
\[\frac{110}{100}=\frac{121}{x}\]
\[x=\frac{121\cdot 100}{110}\]
\[x=\frac{121\cdot 10}{11}\]
\[x=11\cdot 10\]
\[x=110\]
Esto se interpreta como un aumento de 10%, pues pasamos de 100 a 110.
Letra B.
P17

Solución:
La opción correcta es la D, ya que la división de potencias puede realizarse por medio de propiedades siempre que las bases o los exponentes sean iguales, con esto asegurado, procedemos a restar los exponentes, el problema sería si nos resulta un exponente negativo ya que en este vaso nuestro resultado sería una fracción (por ejemplo, \(2^{-4}=\frac{1}{16}=0,0625\) lo cual no es un número par.
Letra D.
P18

Solución:
Para responder necesitamos evaluar la función al menos en dos horas distintas, sugiero hacerlo con t = 0 y t = 1, ya que los cálculos serán mucho más fáciles.
\[C(0)=2000\cdot 1,1^0\]
\[C(0)=2000\cdot 1\]
\[C(0)=2000\]
\[C(1)=2000\cdot 1,1^1\]
\[C(1)=2000\cdot 1,1\]
Aquí podemos detenernos, ya que multiplicar la misma cantidad (2000) por el factor 1,1 implica aumentarlo en un 10%. Pueden revisar mi post de porcentajes para profundizar.
Letra C.
P19

Solución:
\[1^0+2^3=\]
\[1+8=\]
\[9\]
Letra A.
P20

Solución:
Para resolver este problema debemos recordar que multiplicar por una potencia de base 10 consiste en añadir ceros según el número del exponente, si el exponente es 4 añadimos 4 ceros y así.
Con esto en mente la correcta es la alternativa C, ya que tendríamos
\[10.000+2.000+50+6=12.056\]
Letra C.
P21

Solución:
Sultán tiene actualmente 5 años y medio, si le añadimos dos años y medio tendrá en total 8 años de vida lo cual equivale a 63.
Letra C.
P22

Solución:
Realizaré un pequeño esquema para calcular la solución
Cantidad de kilos por caja: 7
Cantidad de cajas por almacén: 7
Cantidad de almacenes: 7
Días de la semana: 7
Para resolver multiplicamos estos valores
\[7\cdot7\cdot7\cdot7=7^4\]
Letra C.
P23

Solución:
Para resolver basta con reemplazar la cantidad de años en x, resultando
\[2\cdot2^4=\]
\[2^5=\]
\[32\]
Letra B.
P24

Solución:
Para resolver podemos factorizar (que dos números sumados dan 5 y multiplicados -6) o bien probar con las alternativas multiplicando término a término. Haré lo primero.
\[x^2+5x-6\]
\[x_1+x_2=5\]
\[x_1\cdot x_2 =-6\]
Los números son 6 y -1, multiplicados dan -6 y sumados 5. La expresión queda:
\[(x-1)(x+6)\]
Letra B.
P25

Solución:
Resolvamos y reduzcamos los términos semejantes para averiguarlo
\[\frac{1}{2}(-b-(b-2)+2)=\]
\[\frac{1}{2}(-b-b+2+2)=\]
\[\frac{1}{2}(-2b+4)=\]
\[\frac{-2b}{2}+\frac{4}{2}=\]
\[-b+2\]
Letra D.
P26

Solución:
Multiplicamos directamente, pero transformamos los kg a gr, si tienen dudas sobre como multiplicar decimales, vean mi post :D.
\[83\cdot 0,05=\]
\[4,15\]
Letra B.
P27

Solución:
Si planteamos una proporción podemos despejar la incógnita que necesitamos
\[\frac{pulgada}{cm}=\frac{2}{5,1}=\frac{x}{cm}\]
de aquí despejaremos los «cm»
\[cm=\frac{5,1}{2}x\]
Letra A.
P28

Solución:
Para resolver debemos reemplazar cuidadosamente los valores dados en la fórmula
\[r=\frac{V}{t}\]
\[1200=\frac{600}{t}\]
\[t=\frac{600}{1200}\]
\[t=\frac{1}{2}\]
Esto corresponde a media hora, es decir, 30 minutos.
Letra C.
P29

Solución:
Resolveremos transformado los 3m en centímetros, \(3m=300cm\), ahora con una ecuación despejamos la incógnita
\[300=x+180+x\]
\[300=2x+180\]
\[120=2x\]
\[60=x\]
Letra B.
P30

Solución:
Para resolver, reemplazamos los datos en nuestra fórmula y despejamos
\[C+V=A+2\]
\[C+8=18+2\]
\[C+8=20\]
\[C=20-8\]
\[C=12\]
Letra A.
P31

Solución:
Para encontrar la medida basta con reemplazar los valores y despejar la incógnita
\[H+2C=64\]
\[30+2C=64\]
\[2C=34\]
\[C=17\]
Letra D.
P32

Solución:
Resolvemos la ecuación
\[3-2x=7\]
\[3=7+2x\]
\[3-7=2x\]
\[-4=2x\]
\[\frac{-4}{2}=x\]
\[-2=x\]
Letra D.
P33

Solución:
El enunciado indica que x es el total del fondo, esto indica además que cada porcentaje se calculará respecto de este total (x), es decir, el 50% de Andrea sería \(\frac{50}{100}x\) y así cada uno, veámoslo en una ecuación
\[\text{Andrea+Benjamin+Diego+Carla}=x\]
\[\frac{50}{100}x+\frac{25}{100}x+\frac{10}{100}x+150.000=x\]
Ahora simplificamos
\[\frac{1}{2}x+\frac{1}{4}x+\frac{1}{10}x+150.000=x\]
Letra C.
P34

Solución:
Para resolver utilizaremos un Sistema de Ecuaciones, siendo «x» la cantidad de billetes de 2.000 e «y» la cantidad de billetes de 10.000, las ecuaciones se plantean pensando en la cantidad total de billetes y la cantidad de dinero.
\[x+y=30\]
\[2.000x+10.000y=100.000\]
Ahora podemos resolver el método que mejor nos parezca, utilizaré sustitución despejando x en la primera ecuación y sustituyéndola en la segunda ecuación
\[x+y=30\]
\[x=30-y\]
Ahora reemplazo en la segunda ecuación
\[2.000x+10.000y=100.000\]
\[2.000(30-y)+10.000y=100.000\]
Resolviendo esta ecuación tendremos la «y», es decir, la cantidad de billetes de 10.000
\[2.000(30-y)+10.000y=100.000\]
\[60.000-2000y+10.000y=100.000\]
\[8.000y=40.000\]
\[y=5\]
Sabiendo que \(y=5\) obtenemos «x»
\[x+y=30\]
\[x+5=30\]
\[x=25\]
Letra B.
P35
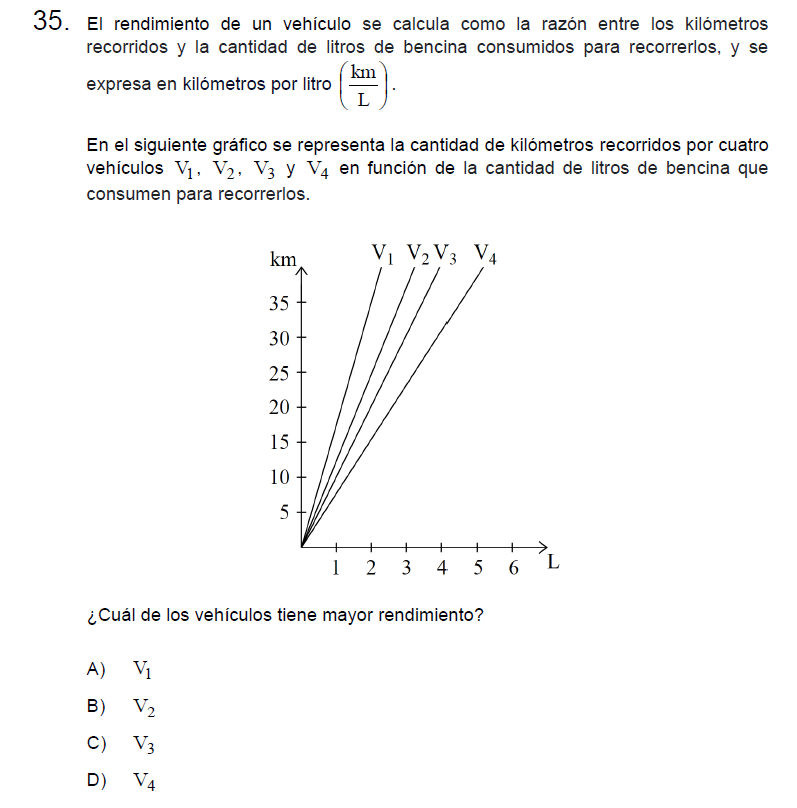
Solución:
Para responder debemos entender que mientras más arriba, más kilómetros, y mientras más a la derecha, más litros de combustible, por lo tanto, el vehículo con mejor rendimiento es aquel que llega más arriba y se queda más a la izquierda, por lo tanto la respuesta correcta es el \(V_1\)
Letra A.
P36

Solución:
Resolveré el sistema utilizando el método de reducción, multiplicaré la primera ecuación por \(-2\):
\[2x+y=6 /\cdot -2\]
\[-4x-2y=-12\]
Con esto tenemos el sistema equivalente
\[-4x-2y=-12\]
\[4x+3y=12\]
Sumamos hacia abajo obteniendo
\[y=0\]
Teniendo el valor de y, procedemos a obtener el de x, reemplazaré en la primera ecuación
\[2x+y=6\]
\[2x+(0)=6\]
\[2x=6\]
\[x=3\]
Letra C.
P37

Solución:
Podemos resolver planteando un sistema de ecuaciones, o bien una ecuación lineal mezclando ambas informaciones, para ello conviene entender la razón dada 1:3 como partes de un total, es decir, el total de personas es equivalente a 4 partes (1+3), siendo así podemos escribir una ecuación utilizando la incógnita x de la siguiente manera
\[x+3x=120\]
\[4x=120\]
\[x=30\]
Lo anterior indica que la cantidad de hombres es 30 y la de mujeres 90.
Letra D.
P38

Solución:
Podemos descartar inmediatamente las alternativas C y D ya que en ellas la cantidad de leche va aumentando y se nos pregunta cuánto líquido queda en el envase (100 ml). El gráfico de B, al ser una línea «contínua», indica que el líquido ha ido descendiendo a lo largo de un periodo más amplio de tiempo y no en un momento puntual, este es el motivo por el cual descarto esta alternativa y escojo la A, en la cual se hace un bajón abrupto del nivel de líquido en los momentos mencionados.
Letra A.
P39

Solución:
Debemos aplicar los porcentajes de descuento y aumento a los precios de la primera empresa.
Un 30% menos de la visita domiciliaria sería obtener el 70% del precio de la primera empresa.
\[70% de 10.000\to \frac{70}{100}\cdot 10.000=7.000\]
Ahora aumentados el 20% por hora trabajada
\[120% de 15.000\to \frac{120}{100}\cdot 15.000=18.000\]
\[h(t)=7.000+18.000t\]
Letra C.
P40

Solución:
Para resolver evaluamos en 60 ambas funciones y las igualamos, de esta igualdad podremos despejar «p».
\[f(60)=1000+25(60)\]
\[f(60)=2500\]
\[g(60)=p+15(60)\]
\[g(60)=p+900\]
Ahora igualamos ambas
\[2500=p+900\]
\[1600=p\]
Letra C.
P41

Solución:
Su error está en el paso dos ya que al multiplicar por -100, olvida cambiar el signo de «y»
Letra B.
P42

Solución:
El área de un triángulo rectángulo se obtiene multiplicando las medidas de sus catetos y dividiendo por 2, si definimos que el cateto menor es «x» y el cateto mayor es «x+3».
\[54=\frac{x(x+3)}{2}\]
\[108=x(x+3)\]
\[108=x^2+3x\]
\[0=x^2+3x-108\]
Nos queda una ecuación cuadrática, vamos a resolverla
\[0=(x+12)(x-9)\]
\[x_1=-12\]
\[x_2=9\]
Nos quedamos con la respuesta positiva, por lo tanto el cateto mayor mide 9+3=12
Letra C.
P43

Solución:
Basta con contar pero de igual manera lo explicaré, de abajo hacia arriba tenemos 9 cajas, luego 6 cajas, luego 4 cajas y luego 1.
\[9+6+4+1=20\]
Letra D.
P44

Solución:
Para resolver obtendremos la capacidad total del estanque y luego la dividiremos en 2 (50%).
Recordemos la fórmula: \(\pi \cdot r^2\cdot h\)
\[V=3\cdot 2^2 \cdot 4\]
\[V=3\cdot 4 \cdot 4\]
\[V=48\]
El volumen total es 48 y si se utiliza solo la mitad diariamente, entonces la respuesta es 24.
Letra C.
P45
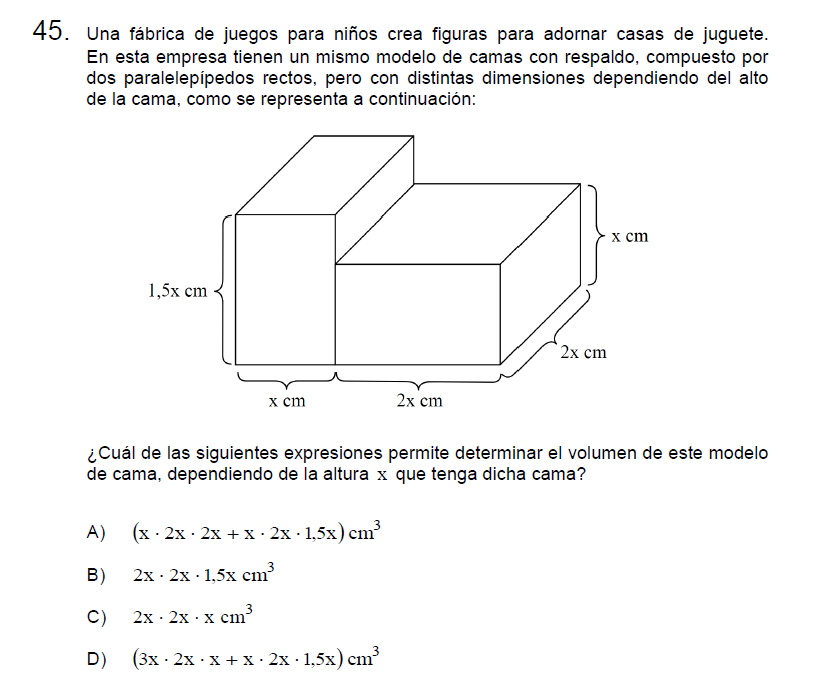
Solución:
Obtendremos el volumen de cada pieza por separado y luego las sumaremos.
Volumen del respaldo:
\[V=1.5x\cdot x\cdot 2x\]
Volumen de la base:
\[V= x \cdot 2x \cdot 2x \]
Si las sumamos obtenemos
\[x \cdot 2x \cdot 2x +1.5x\cdot x\cdot 2x\]
Letra A.
P46
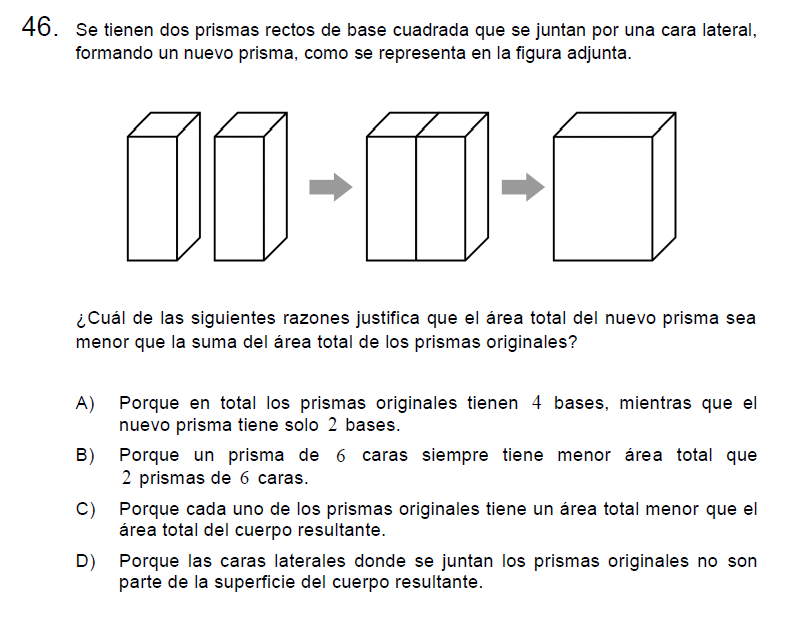
Solución:
Al unir ambos prismas se pierde una cara.
Letra D.
P47
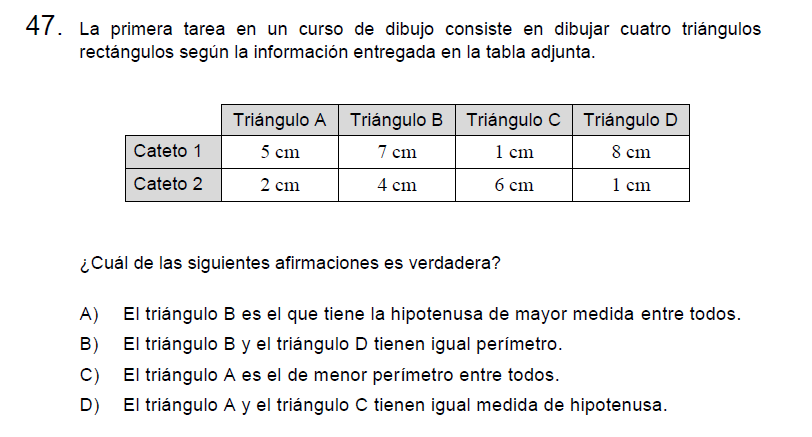
Solución:
Para analizar las distintas afirmaciones debemos determinar las hipotenusas de todos los triángulos, para ello usamos el Teorema de Pitágoras
\[h_A=\sqrt{5^2+2^2}=\sqrt{29}\]
\[h_B=\sqrt{7^2+4^2}=\sqrt{65}\]
\[h_C=\sqrt{1^2+6^2}=\sqrt{37}\]
\[h_D=\sqrt{8^2+1^2}=\sqrt{65}\]
Con esto en listo veamos las alternativas
A: Falso! Ya que es igual a la de D.
B: Falso! Ya que la suma de sus catetos difiere.
C: CORRECTO! ya que sus catetos suman 7 y posee la menor hipotenusa.
Letra C.
P48
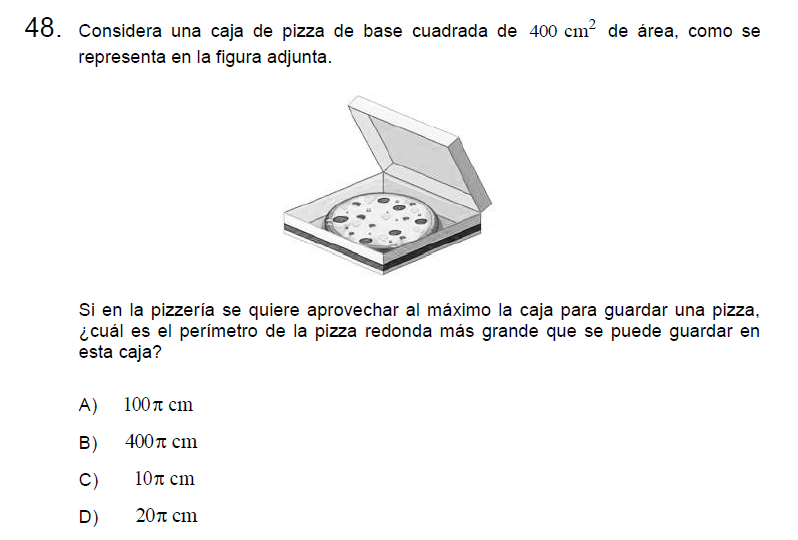
Solución:
Si la base es cuadrada y su área es 400 indica que su lado mide 20 cm, siendo así el radio máximo de la pizza es de 10 cm, con esta información podemos obtener su perímetro.
\[P=2\pi \cdot 10\]
\[P=20\pi \]
Letra D.
P49

Solución:
Si el triángulo es rectángulo e isósceles de área 72, podemos obtener las medidas de los catetos
\[72=\frac{x\cdot x}{2}\]
\[144=x^2\]
\[12=x\]
La medida de los catetos es 12
con esto podemos obtener la hipotenusa con Pitágoras (aunque si conocen bien la materia saben inmediatamente que la hipotenusa es \(12\sqrt{2}\))
\[h=\sqrt{12^2+12^2}\]
\[h=\sqrt{144+144}\]
\[h=\sqrt{2(144)}\]
\[h=12\sqrt{2}\]
Por lo tanto el perímetro es
\[P=24+12\sqrt{2}\]
Letra B.
P50

Solución:
La opción correcta es D, puesto que se necesitan 3 diámetros y algunos decimales más (\pi) para cubrir el perímetro de la circunferencia, sin embargo, podemos explicarlo haciendo una división:
\[\frac{\text{perímetro}}{diámetro}=\frac{2\pi r}{2r}=\pi=3,14…\]
Letra D.
P51

Solución:
Veamos donde terminó la tienda desde su punto original (7,5)
\[(7,5)+(2,-3)+(-3,10)=(7+2+(-3),5+(-3)+10)=(6,12)\]
Esto significa doce cuadras al norte y seis al este.
Letra B.
P52

Solución:
Aplicamos el vector traslación al punto original, para ello sumamos coordenada a coordenada:
\[(1,-2)+(-5,-3)=(1+-5,-2+-3)=(-4,-5)\]
Letra C.
P53

Solución:
Veamos donde queda el nuevo centro,
\[(-1,-2)+(3,4)=(2,2)\]
A este centro se le aplica una reflexión en torno al eje Y, por lo tanto, cambia su coordenada x, resultando el punto
\[(-2,2)\]
Siendo este el nuevo centro, podemos verificar si los puntos pertenecen o no, ya que sabemos que su radio es 1 unidad.
El punto \((-2,3)\) pertenece a esta circunferencia ya que se aleja 1 unidad hacia arriba del centro.
Letra B.
P54
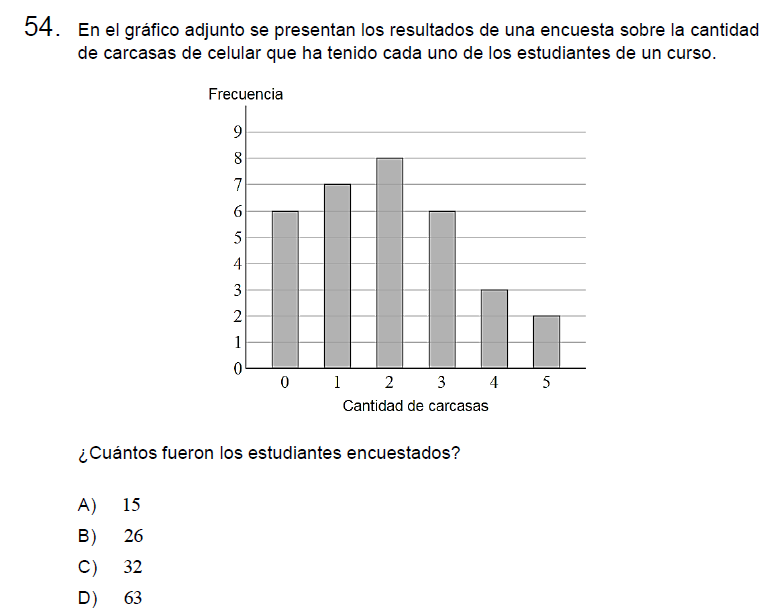
Solución:
Para responder basta con sumar las frecuencias de cada barra, es decir,
\[6+7+8+6+3+2=32\]
Letra C.
P55
Solución:
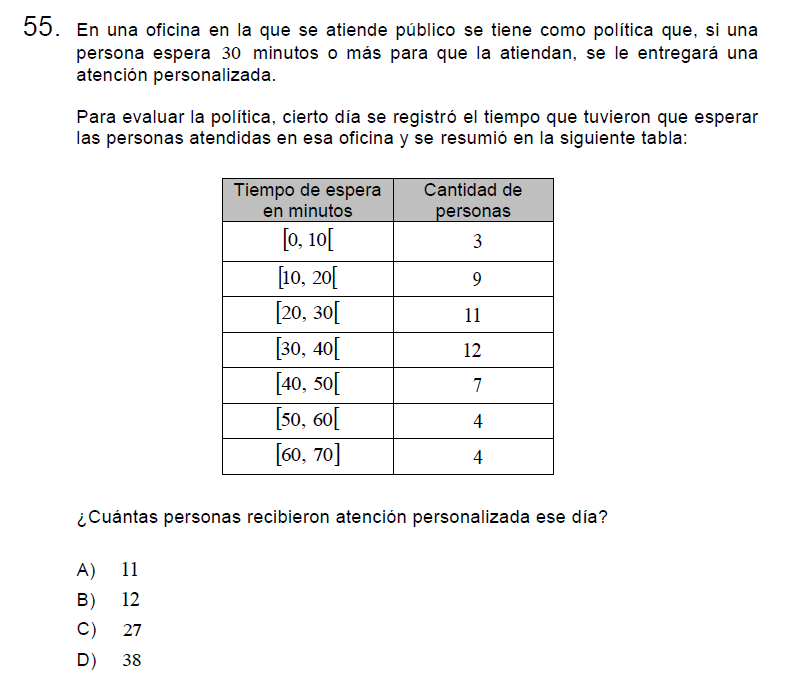
Los que esperaron 30 minutos o más son aquellos que inician en la cuarta fila de los intervalos [30,40[ desde este punto sumamos las frecuencias pues dice «o más»
\[12+7+4+4=27\]
Letra C.
P56

Solución:
Vamos avanzando por alternativa
A: Falso! ya que nos habla de un promedio, por ejemplo podríamos tener una persona con 9 años de estudio y una con 5, el promedio sería 7, sin embargo, solo uno de ellos tendría más de 7 años de escolaridad.
B: Falso ya que Ñuble tiene un 6,4
C: Para comprobar esto debemos calcular el 8,5% de 123.201, esto es:
\[\frac{8,5}{100}\cdot 123.201=10.472,08\]
Esta es la alternativa correcta ya que aproximadamente coinciden los números.
D: Falso! ya que las mujeres son un 22,8% más.
Letra C.
P57

Solución:
Obtengamos en primer lugar el promedio con estos datos
\[\bar{x}=\frac{4+6+8+10+12}{5}\]
\[\bar{x}=\frac{40}{5}\]
\[\bar{x}=8\]
Podemos darnos cuenta de que los datos avanzan de dos en dos quedando el 8 en el centro, no es casualidad, es por esta razón que el promedio es también 8. Podemos buscar una pareja de datos que se encuentren a 2 unidades de distancia del dato menor y 2 unidades de distancia del dato mayor, es decir, el 2 y el 14.
Si quieren comprobar, añadamos estos números y calculemos el promedio
\[\bar{x}=\frac{40+2+14}{7}\]
\[\bar{x}=\frac{56}{7}\]
\[\bar{x}=8\]
Letra D.
P58
Solución:
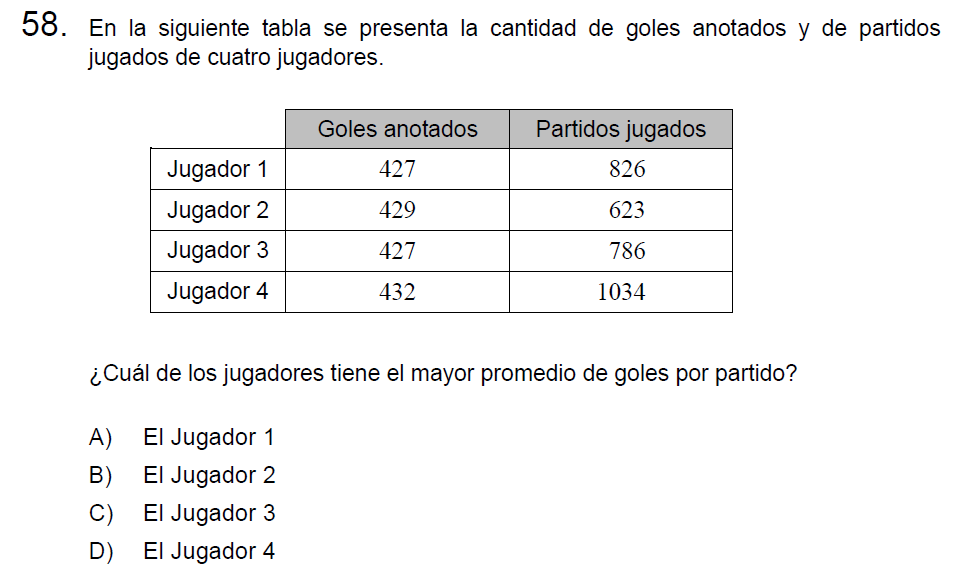
El jugador que tiene mayor promedio es aquel que ha anotado más goles en una menor cantidad de partidos por lo tanto el jugador 4 sin realizar cálculos sería el menor promedio y el jugador 2 es aquel con mayor promedio ya que fue quien anotó más goles en menos partidos.
Letra B.
P59
Solución:
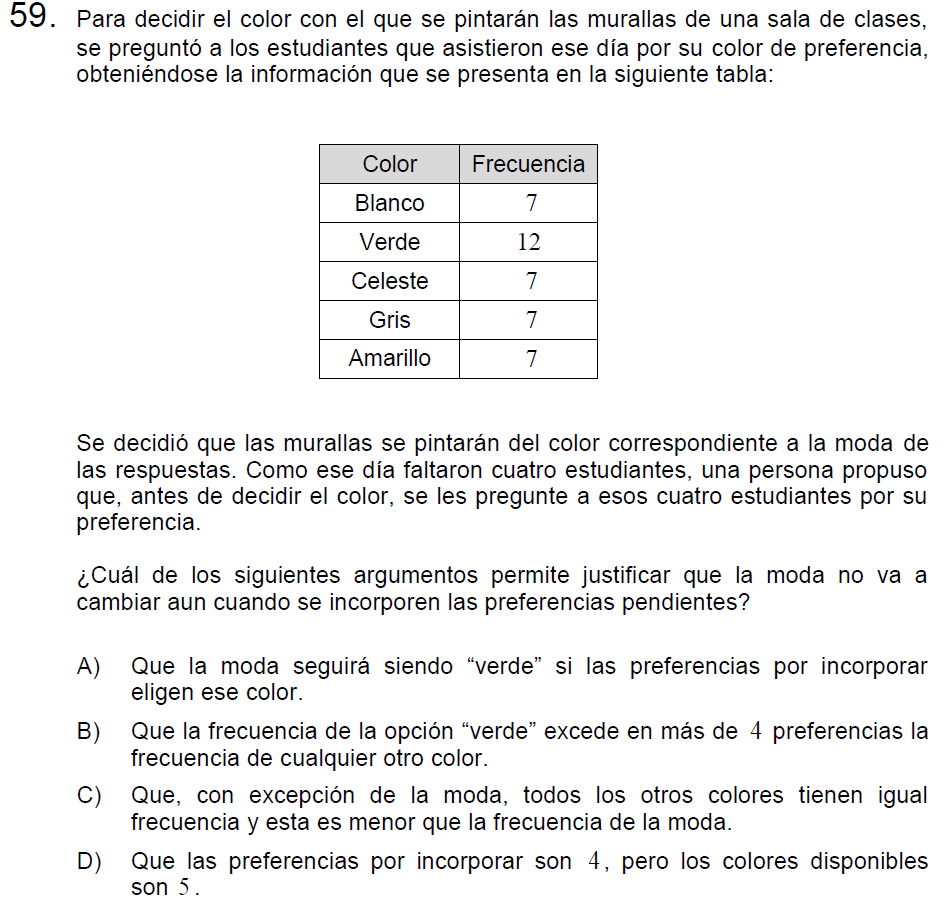
Traduciendo la opción correcta (B): «para que cualquier otra opción alcance la frecuencia del Verde se debería sumar 5 y solo había 4 estudiantes ausentes».
Letra B.
P60

Solución:
Calculemos todas las desviaciones
\(3,01-2,994=0,016\)
\(3,01-2,994=0,016\)
\(2,98-2,994=-0,014\)
\(2,97-2,994=-0,024\)
\(3-2,994=0,006\)
Para encontrar la mediana ordenamos los datos de menor a mayor
\[-0.024, -0.014, 0.006, 0.016, 0.016\]
La mediana sería el término central, es decir,
\[0.006\]
Letra D.
P61

Solución:
Para entender las opciones podemos plantear las fórmulas de promedio, lo que corresponda a la primera sucursal irá con un 1 y la segunda con un 2,
\[\text{promedio}_1=\frac{\text{suma}_1}{n_1}\]
\[550.000=\frac{s_1}{n_1}\]
\[550.000\cdot n_1=s_1\]
\[\text{promedio}_2=\frac{\text{suma}_2}{n_2}\]
Antes de reemplazar recordemos que la sucursal dos tiene el doble de trabajadores que la sucursal 1.
\[450.000=\frac{s_2}{2n_1}\]
\[450.000\cdot 2n_1=s_2\]
\[900.000\cdot n_1=s_2\]
Con esto podemos ver que la suma de los sueldos de los trabajadores de la sucursal dos es mayor que la de los trabajadores de la sucursal uno.
Con lo anterior A es Incorrecta!
Probemos la alternativa B:
Esta opción es incorrecta si consideramos el caso en que todos los trabajadores de la sucursal 1 ganan 550.000 y los trabajadores de la sucursal 2 dividen sus sueldos en igual cantidad entre 500.000 y 400.000, en este caso el promedio serían los correspondientes 450.000 y de esta manera no encontramos un trabajador de la sucursal 1 que gane 100.000 más que cualquier trabajador de la sucursal 2.
Probemos la alternativa C:
El promedio de ambas sucursales se puede obtener con la fórmula
\[\text{Promedio}=\frac{s_1+s_2}{n_1+n_2}\]
\[\text{Promedio}=\frac{s_1+s_2}{n_1+2n_1}\]
\[\text{Promedio}=\frac{550.000\cdot n_1+900.000\cdot n_1}{n_1+2n_1}\]
\[\text{Promedio}=\frac{1.450.000\cdot n_1}{3n_1}\]
\[\text{Promedio}=\frac{1.450.000}{3}\]
\[\text{Promedio}=483.333\]
Por lo anterior, C es incorrecta!
Probemos la alternativa D:
El doble de las sumas de los sueldos de la sucursal 1 es,
\[2\cdot 550.000\cdot n_1=\]
\[1.100.000\cdot n_1=\]
lo cual es mayor que la suma de los sueldo de la sucursal 2, \(900.000\cdot n_1\)
por lo tanto la opción D es correcta!.
Letra D.
P62

Solución:
Para resolver debemos determinar claramente la totalidad de los datos y los que van quedando al realizar las extracciones de lápices
Antes de iniciar:
Escriben: 10
No escriben: 2
Luego de la primera extracción
Escriben: 9
No escriben: 2
Luego de la segunda extracción
Escriben: 9
No escriben: 1
Con esto claro podemos plantear la probabilidad
\[\text{Probabilidad de que no escriba}=\frac{1}{10}\]
Letra B.
P63
Solución:
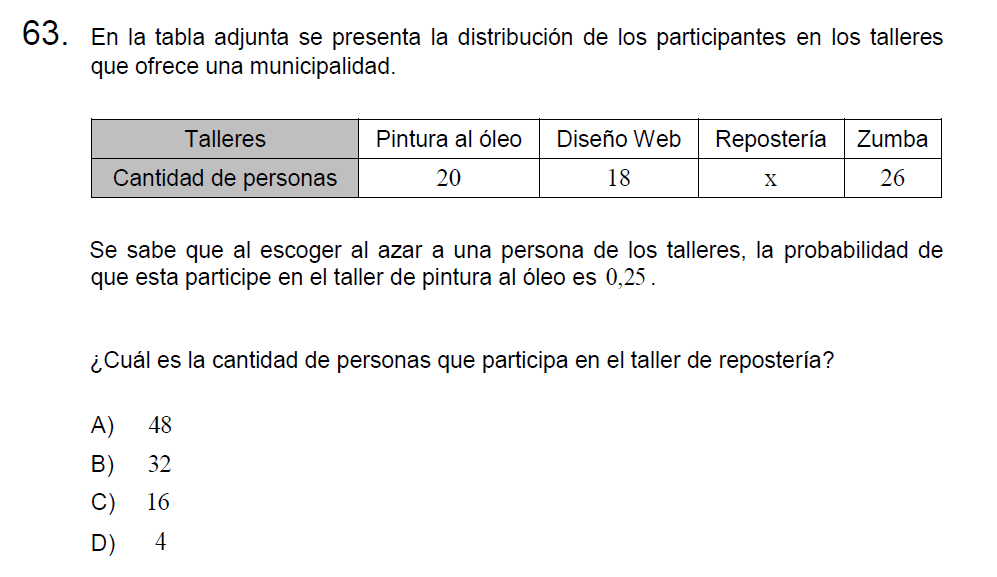
El dato que nos entregan (la probabilidad de que participe en el taller de pintura) nos indica que \(\frac{1}{4}\) del total de personas van a este taller, esto significa que el total de personas es de:
\[4\cdot 20 = 80\]
Sabiendo esto podemos determinar la cantidad de personas que asisten al taller de repostería, esto es la cantidad de personas que faltan para completar los 80.
\[80-(20+18+26)=\]
\[80-64=16\]
Letra C.
P64

Solución:
La información entregada nos permite determinar que la probabilidad de obtener una bolita roja es de \(\frac{1}{3}\), por lo tanto, la cantidad de bolitas rojas es un tercio del total
\[\frac{1}{3}\cdot 36 = 12\]
Letra B.
P65

Solución:
Para saber con exactitud cual es el gráfico que corresponde, debemos encontrar los tres cuartiles
\[Q_1=\frac{25}{100}\cdot 21 = \frac{21}{4}=5,25\]
por lo tanto, \(Q_1=1\)
\[Q_2=\frac{50}{100}\cdot 21 = \frac{21}{2}=10,5\]
por lo tanto, \(Q_2=2\)
\[Q_3=\frac{75}{100}\cdot 21 = 3\cdot \frac{21}{4}=\frac{63}{4}=15,75\]
por lo tanto, \(Q_3=3\)
Letra C.
En el momento en que publico este Post el Demre aún no ha liberado el clavijero con las respuestas correctas por lo que si hubiere algún error les pido que me comenten y yo lo reviso! y si están todas correctas, felicítenme y compartan con sus compañeros.
