Buenas a todos y todas, traigo una nueva temática del ámbito de la estadística y organización de datos. Las tablas de frecuencias, son, como su nombre lo indica, tablas que resumen una gran cantidad de datos (frecuencias), nos sintetizan y permiten analizar grandes cantidades de información. Por ejemplo, podemos utilizarlas para presentar la información recopilada al preguntar a un grupo de personas su Peso, su estatura o su IMC.
Iremos construyendo las distintas columnas que pueden aparecer en una tabla de frecuencia a nivel escolar, daremos un ejemplo sencillo, sin mucho contexto, pero de rápida comprensión.
Ejemplo: ¿Cantidad de lápices que tiene en su estuche?
Se realiza la pregunta anterior a un grupo de 20 personas obteniendo las siguientes respuestas,
1 – 1 – 1 – 1 – 1- 2 – 2 – 2 – 2 – 2 – 2 – 3 – 3 – 3 – 3 – 4 – 4 – 5 – 5 – 5.
Claramente no podemos trabajar con la información presentada de esta manera.
Frecuencia Absoluta
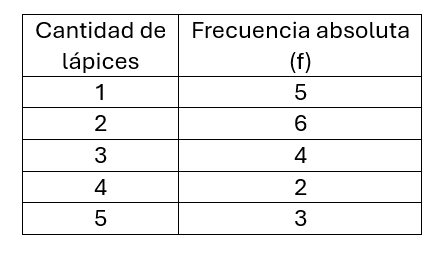
En esta primera etapa presentamos en la primera columna (la de la izquierda) las cinco opciones elegidas por el grupo de personas y en la segunda la «Frecuencia Absoluta».
La frecuencia absoluta nos muestra cuantas personas han seleccionado la opción presentada, en nuestro ejemplo, podemos entender que 6 personas han dicho Amarillo, por lo general se utiliza una f minúscula para representarla pero esto dependerá del libro y el profesor, lo importante es entender que significa.
A partir de la frecuencia absoluta podemos ir construyendo otros tipos de frecuencias.
Frecuencia absoluta acumulada
La frecuencia absoluta acumulada como su nombre lo indica, va acumulando, va sumando a la frecuencia anterior la nueva frecuencia, los datos deben estar ordenados de menor a mayor, por lo tanto, solo la podemos utilizar con claridad en variables de tipo cuantitativas.

La ultima fila de esta columna (el 20) nos señala la cantidad total de personas que respondieron (n), por lo general representamos al total de personas con la letra «n» y a la frecuencia absoluta acumulada con la letra F (mayúscula).
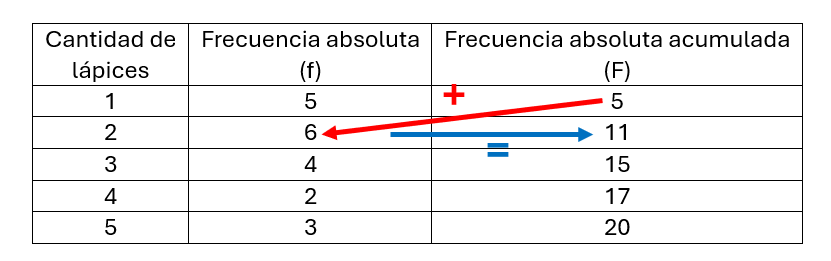
En la tabla anterior se ve el procedimiento para obtener el valor siguiente.
Frecuencia relativa
La frecuencia relativa es una comparación entre la frecuencia absoluta del dato y el total del dato, claramente esto resultará en un número decimal.
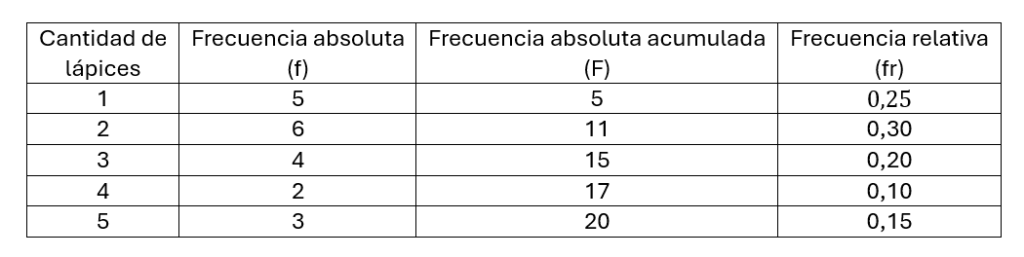
La primera fila se obtendría dividiendo el 5 entre 20, y así sucesivamente.

La suma total de las frecuencias relativas debe ser 1, aunque si se han aproximado decimales, debería ser un valor muy cercano a 1.
Frecuencia relativa acumulada
Esta frecuencia funciona de la misma manera que la absoluta acumulada, solo que depende de la frecuencia relativa. De igual manera la escribiremos con mayúscula «Fr».
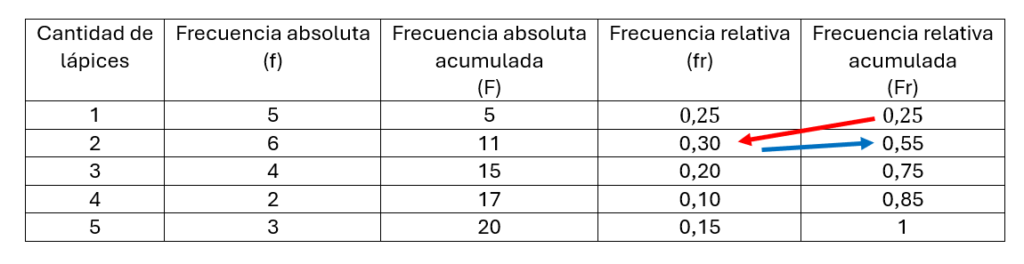
Frecuencia relativa porcentual o Frecuencia porcentual
Esta frecuencia nos muestra que porcentaje del total representa cada frecuencia absoluta, podemos calcularlo muy fácilmente si ya conocemos la frecuencia relativa, solo multiplicas por 100 (o correr la coma 2 espacios).
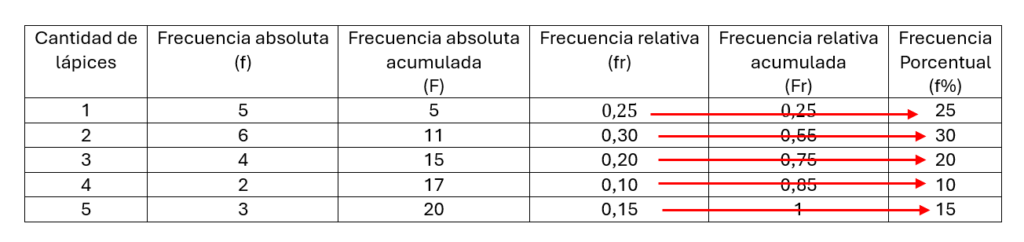
La suma de todas estas frecuencias porcentuales debe ser 100 o muy cerca si es que hemos aproximado valores.
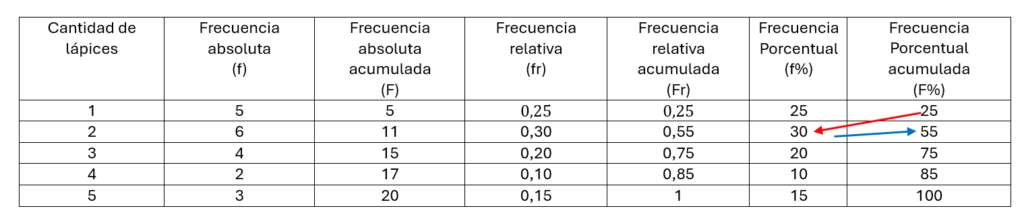
Frecuencia relativa porcentual acumulada
La última columna que veremos es la acumulada de la porcentual, funciona igual que todas las acumuladas anteriores.
Ejercicio resuelto
Determine los valores faltantes en la siguiente tabla de frecuencias.
| Variable (xi) | Frecuencia absoluta (ni) | Frecuencia relativa hi | Frecuencia absoluta acumulada (Ni) |
| x1=2 | n1= | h1= | N1=12 |
| x2=10 | n2= | h2=0,5 | N2= |
| x3=5 | n3= | h3= | N3=47 |
| x4=0 | n4=3 | h4= | N4= |
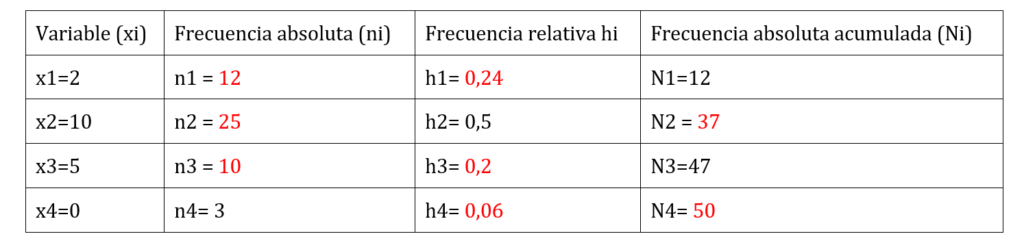
Solución:
Podemos obtener N4 sabiendo que es el resultado de sumar 47 + 3, pues es una frecuencia acumulada.

Ahora podemos obtener n2 sabiendo que su frecuencia relativa es 0,5, esa frecuencia indica que representa la mitad de la totalidad de los datos, es decir, la mitad de 50.

Podemos seguir con N2, ya que es una frecuencia acumulada, es el resultado de sumar 12 con 25.

Ahora, n3 resulta de preguntarse ¿37 más cuánto da 47?.

Podemos repetir N1 en n1 ya que ambos coinciden.

Finalmente calculamos todas las frecuencias relativas dividiendo sus frecuencias absolutas entre 50, por ejemplo \(h1 = 12 : 50\)
A partir de estas tablas pueden hacerse otros análisis, como por ejemplo, obtener las Medidas de Tendencia Central (media, moda y mediana), sin embargo, estudiaremos aquello en un post específico.

Pingback: Medidas de tendencia central – Mates pal Colegio
Pingback: ¿Qué entra en la PAES M1 de Invierno 2024? - Mates pal Colegio