¿Alguna vez te has preguntado cómo los arquitectos diseñan edificios perfectamente rectos? ¿O cómo los carpinteros aseguran que sus muebles tengan esquinas en ángulo recto? ¿Y qué hay de los ingenieros que construyen puentes o los diseñadores de videojuegos que crean mundos virtuales? Todos ellos tienen un aliado secreto en común: el Teorema de Pitágoras.
Este teorema, que lleva el nombre de un matemático griego que vivió hace más de 2500 años, es mucho más que una simple fórmula que memorizamos para los exámenes. Es una herramienta poderosa que ha ayudado a la humanidad a construir ciudades, navegar por los océanos e incluso explorar el espacio. Con él, puedes resolver misterios geométricos que se esconden en triángulos rectángulos, desde calcular la altura del Costanera Center de Santiago hasta determinar la longitud perfecta de una rampa para tu skate.
Descubriremos cómo una simple ecuación puede desbloquear secretos del universo y ayudarte en tu vida cotidiana. ¡Vamos a ello!
Definición del Teorema de Pitágoras
Para empezar, es esencial entender qué es un teorema. En términos simples, un teorema es una afirmación que puede ser demostrada lógicamente a partir de reglas establecidas. En este teorema propuesto por Pitágoras o algún miembro de su escuela, se relacionan las medidas de los lados de un triángulo rectángulo. El teorema establece que:
«El cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos»
Ejemplo: Imagina que quieres medir la longitud de una escalera que necesitas para alcanzar una plataforma elevada. Sabes que la plataforma está a 3 metros de altura y la base de la escalera se encuentra a 4 metros de la pared. Usando el Teorema de Pitágoras, puedes calcular la longitud de la escalera:
\[ c^2 = 3^2 + 4^2 \] \[ c^2 = 9 + 16 \] \[ c^2 = 25 \] \[ c = 5 \]
Así, necesitas una escalera de 5 metros de longitud.
¿Qué es un triángulo rectángulo?
Un triángulo rectángulo es un triángulo que tiene un ángulo recto, es decir, un ángulo de 90°. Los lados del triángulo se denominan catetos e hipotenusa, siendo esta última el lado opuesto al ángulo recto y el más largo del triángulo. Representamos las medidas de los lados con las letras a, b y c, donde c es la hipotenusa y a y b son los catetos.
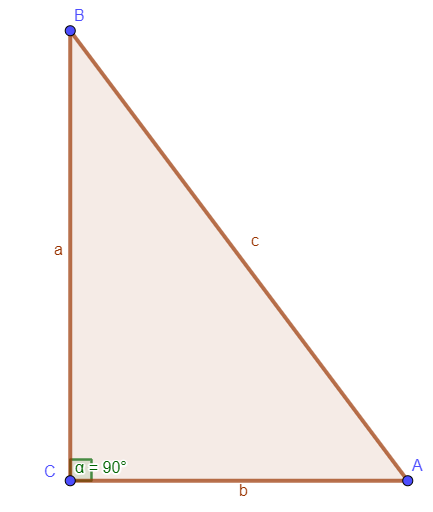
Con las letras otorgadas el Teorema de Pitágoras queda expresado como:
\[c^2=a^2+b^2\]
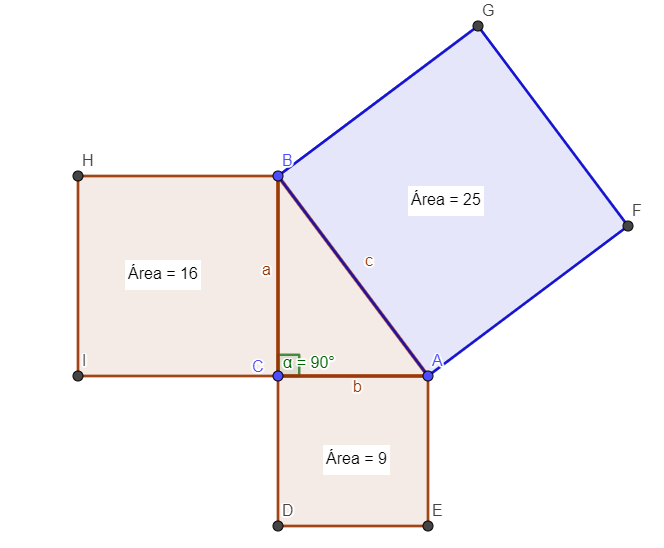
Veamos una imagen más sobre esto:
Video Explicativo
En este video veremos un Demostración del Teorema de Pitágoras, espero que al verlo les ayude y les quede aún más claro todo!
Ejemplo: Si estás construyendo una rampa para acceso a una entrada, y la rampa necesita tener un ángulo recto con el suelo. La rampa tiene que elevarse 1 metro y la base de la rampa está a 4 metros de la entrada. Puedes calcular la longitud de la rampa:
\[ c^2 = 1^2 + 4^2 \] \[ c^2 = 1 + 16 \] \[ c^2 = 17 \] \[ c = \sqrt{17} \approx 4.12 \]
La longitud de la rampa será aproximadamente 4.12 metros.
Teorema Inverso o Recíproco del Teorema de Pitágoras
El teorema inverso establece que:
«Si en un triángulo, el cuadrado del lado más largo es igual a la suma de los cuadrados de los otros dos lados, entonces el triángulo es rectángulo».
Este teorema es muy útil en construcción. Por ejemplo, para asegurar que una esquina es un ángulo recto, se puede medir 3 metros en un lado y 4 metros en el otro; si la diagonal mide 5 metros, se forma un triángulo rectángulo (un trío pitagórico).
Ejemplo: Un carpintero quiere asegurarse de que una mesa está perfectamente cuadrada. Mide 6 pies en un lado y 8 pies en el otro. Para confirmar que la mesa está cuadrada, la diagonal debería medir 10 pies:
\[ 10^2 = 6^2 + 8^2 \] \[ 100 = 36 + 64 \] \[ 100 = 100 \]
Tríos Pitagóricos
Existen varios tríos pitagóricos que podemos memorizar para facilitar cálculos rápidos. Algunos de los más comunes son:
- 3, 4, 5
- 5, 12, 13
- 8, 15, 17
Ejemplo con el Trío 3, 4, 5
Demostremos que este trío cumple con el Teorema de Pitágoras:
\[ 5^2 = 3^2 + 4^2 \] \[ 25 = 9 + 16 \] \[ 25 = 25 \]
Funciona perfecto. Podemos crear otros triángulos multiplicando cada lado por el mismo factor. Por ejemplo, multiplicando por 2:
\[ (3 \times 2), (4 \times 2), (5 \times 2) = 6, 8, 10 \] \[ 10^2 = 6^2 + 8^2 \] \[ 100 = 36 + 64 \] \[ 100 = 100 \]
Ejemplo: Si estás diseñando un jardín y quieres crear una sección triangular con lados de 3 metros, 4 metros y 5 metros para asegurarte de que sea un triángulo rectángulo perfecto, puedes utilizar este trío pitagórico y así tener certeza de que el ángulo es de 90 grados.
Calcular la Hipotenusa y los Catetos
Ya hemos visto cómo calcular la hipotenusa. Ahora veamos algunos ejemplos adicionales.
Calcula la Hipotenusa
Si los catetos miden 8 cm y 15 cm, la hipotenusa se calcula así:
\[ c^2 = 8^2 + 15^2 \] \[ c^2 = 64 + 225 \] \[ c^2 = 289 \] \[ c = 17 \]
(En el último paso, calculamos la raíz cuadrada de 289)
La hipotenusa mide 17 cm.
Ejemplo: Si necesitas medir la diagonal de un televisor rectangular, y conoces las dimensiones de la pantalla, puedes usar el teorema para calcularla. Por ejemplo, si la pantalla mide 24 pulgadas de alto y 32 pulgadas de ancho, la diagonal será:
\[ c^2 = 24^2 + 32^2 \] \[ c^2 = 576 + 1024 \] \[ c^2 = 1600 \] \[ c = 40 \]
La diagonal del televisor es de 40 pulgadas.
Calcular un Cateto
Si un cateto mide 12 cm y la hipotenusa mide 15 cm, ¿cuánto mide el otro cateto?
\[ 15^2 = 12^2 + b^2 \] \[ 225 = 144 + b^2 \] \[225-144=b^2\] \[ 81 = b^2 \] \[ b = 9 \]
El cateto mide 9 cm.
Ejemplo: Si estás instalando una antena de TV y la antena se coloca en un punto a 15 metros de altura y la cuerda que la sujeta a tierra está a 12 metros de distancia de la base del mástil, puedes calcular la altura a la que la cuerda se sujeta al mástil:
\[ 15^2 = 12^2 + b^2 \] \[ 225 = 144 + b^2 \] \[225-144=b^2\] \[ 81 = b^2 \] \[ b = 9 \]
La cuerda se sujeta al mástil a 9 metros de altura.
Ejercicios con el Teorema de Pitágoras
Veamos algunos ejercicios en los que debemos utilizar el Teorema de Pitágoras, busqué varios que aparecieran en PAES 😀
Ejercicio I
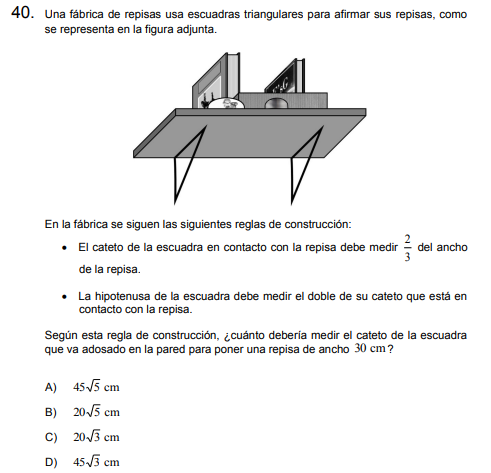
Solución: Letra C.
Tenemos un triángulo rectángulo y directamente nos indican que debemos calcular la medida de uno de los catetos, la dificultad está en ir descubriendo las medidas con la información dada.
Se nos dice que el cateto en contacto con la repisa es \(\frac{2}{3}\) del ancho de la repisa, es decir, de 30 cm.
\[\frac{2}{3}\cdot 30=20\]
El cateto mide 20 cm.
La hipotenusa mide el doble que este cateto, es decir, 40 cm.
Con esta información planteamos la ecuación (con Pitágoras) y descubrimos la medida faltante
\[40^2=20^2+b^2\]
\[1600=400+b^2\]
\[1200=b^2\]
\[\sqrt{1200}=b\]
\[\sqrt{4\cdot 100\cdot 3}=b\]
\[2\cdot 10\sqrt{3}=b\]
\[20\sqrt{3}\]
Ejercicio II

Solución: Letra A.
En este caso nos dan a conocer un cateto y la hipotenusa, planteamos Pitágoras y obtenemos la medida faltante.
\[15^2=12^2+b^2\]
\[225=144+b^2\]
\[81=b^2\]
\[9=b\]
Ejercicio III

Solución: Letra C.
Para resolver determinamos la cantidad de metros que requiere para confeccionar un logo y luego dividimos el total de metros en esta cantidad.
En ambos casos se nos presentan tríos pitagóricos, los catetos miden 3 y 4 por lo tanto su hipotenusa mide 5 metros.
Cantidad de metros para la N:
\[4+4+5=13\]
Cantidad de metros para la X:
\[5+5=10\]
El logo completo utiliza 23 metros
Por lo tanto, con los 50 metros que tiene puede crear solo dos logos.
Ejercicio IV
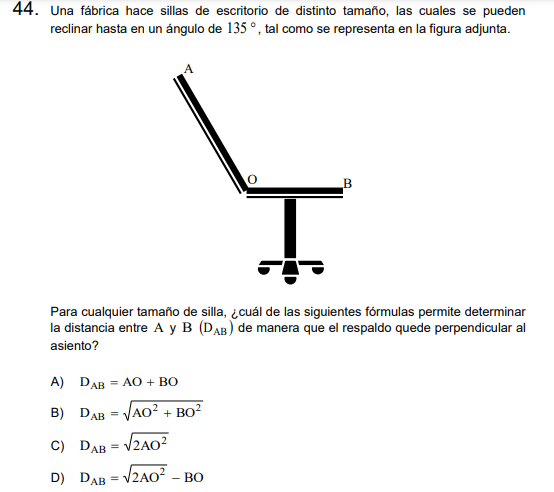
Solución: Letra B.
Aquí debemos utilizar el Teorema Recíproco de Pitágoras.
Si se cumple la relación, entonces podemos asegurar que el ángulo formado es recto (perpendicular).
La ecuación está despejada y la hipotenusa (Distancia de A a B) queda en la izquierda, los catetos son \(AO\) y \(BO\).
\[D_{AB}=\sqrt{AO^2+OB^2}\]
Ejercicio V

Solución: Letra A.
Como las cajas son cubos, cada una de sus aristas mide lo mismo, por lo tanto podemos reducir el problema a determinar la diagonal de un cuadrado de lado \(h\)
Quiero resumir aún mas el problema en calcular la hipotenusa de un triángulo rectángulo isósceles (ambos catetos miden lo mismo).
Planteamos la ecuación:
\[d^2=h^2+h^2\]
Debemos despejar \(d\)
\[d^2=2h^2\]
\[d=\sqrt{2h^2}\]
\[d=h\sqrt{2}\]

Pingback: PAES M1 Invierno 2024 – Mates pal Colegio
Pingback: Puntos, Vectores y transformaciones isométricas – Mates pal Colegio