Hola!! vuelvo nuevamente con otra PAES m1 resuelta y sin costo para ustedes, espero que mis explicaciones sean claras y si tienen dudas, busquen a otro!, NOO era broma 😂🤣, pueden dejarme sus preguntas en la caja de comentarios e iré respondiendo todas sus dudas. Espero que les sirva para prepararse para la PAES, si se lo proponen pueden resolverlo muy a conciencia y comparar sus respuesta, tal como si fuera su intensivo PAES de Matemática!!
P1

Solución:
Vamos realizando paso a paso
\[3-(-1)(-1-5)=\]
\[3-(-1)(-6)=\]
\[3-(+6)=\]
\[3-6=\]
\[-3\]
Letra B.
P2

Solución:
Les dejaré una imagen con el paso a paso, fui resolviendo de izquierda a derecha y luego de arriba a abajo:

Letra C.
P3

Solución:
Nuevamente, vamos paso a paso
\[5\cdot -10\]
\[5\cdot -10-3\cdot -12=\]
\[-50-3\cdot -12=\]
\[-50+36=\]
\[-14\]
Letra B.
P4

Solución:
Paso a Paso sería
\[2\cdot\]
\[2\cdot \frac{1}{3}\]
\[2\cdot \frac{1}{3}\cdot ( – )\]
\[2\cdot \frac{1}{3}\cdot (8 – 6)\]
Importante el paréntesis, de no colocarlo, se entiende que el doble de la tercera parte se calcularía solamente al 8 y no a la diferencia.
Letra B.
P5
Solución:
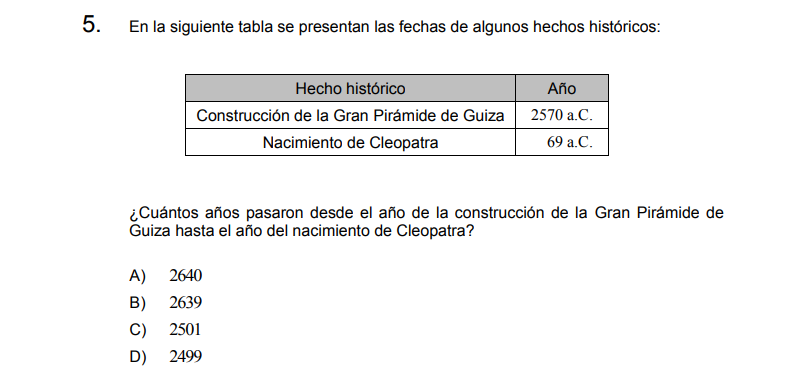
Como ambas fechas son a.C. podemos simplemente calcular la diferencia (resta) entre ellas para obtener la cantidad de años que transcurrieron de un evento a otro
\[2570-69=\]
\[2501\]
Letra C.
P6

Solución:
Vamos a calcular los resultados de cada uno por separado
Pedro: \(4\cdot 10 + 2 \cdot 5 +4\cdot 0 = 40 +10 + 0 = 50\)
Sandra: \(3\cdot 10 + 5 \cdot 5 + 2 \cdot 0 = 30 + 25 + 0 = 55\)
Roberta: \(2\cdot 10 + 8 \cdot 5 +0 \cdot 0 = 20 + 40 + 0 = 60\)
Roberta y Pedro (mayor y menor)
Letra B.
P7

Solución:
Para resolver, a los 300 mil iniciales iremos restando los pagos y las comisiones
\[300.000-15.000-35.000-2.000-2.000=\]
\[300.000-54.000=\]
\[246.000\]
Letra D
P8

Solución:
Para resolver calcularemos cada una de las fracciones antes de avanzar
Primero \(\frac{1}{6}\) de 180
\[\frac{1}{6}\cdot 180 = 30\]
Por lo tanto, 30 pertenecen al Segundo B.
Luego \(\frac{1}{10}\) de 30
\[\frac{1}{10}\cdot 30 = 3\]
Por lo tanto, ese día solo hubo 27 estudiantes.
Finalmente \(\frac{1}{3}\) de 27
\[\frac{1}{3}\cdot 27 = 9\]
Por lo tanto, 18 votaron por Fernando.
Letra B.
P9

Solución:
Cada uno de los cálculos debemos realizarlos según el intervalo que corresponda
Para las 150 el precio es de 20 pesos, para las 130 el precio es de 25 pesos y para las 85 el precio es de 30 pesos por hoja respectivamente, tenemos entonces que
\[150\cdot 20 + 130 \cdot 25 + 85 \cdot 30 =\]
\[3.000 + 3.250 + 2.550 =\]
\[8.800\]
Letra C.
P10
Solución:
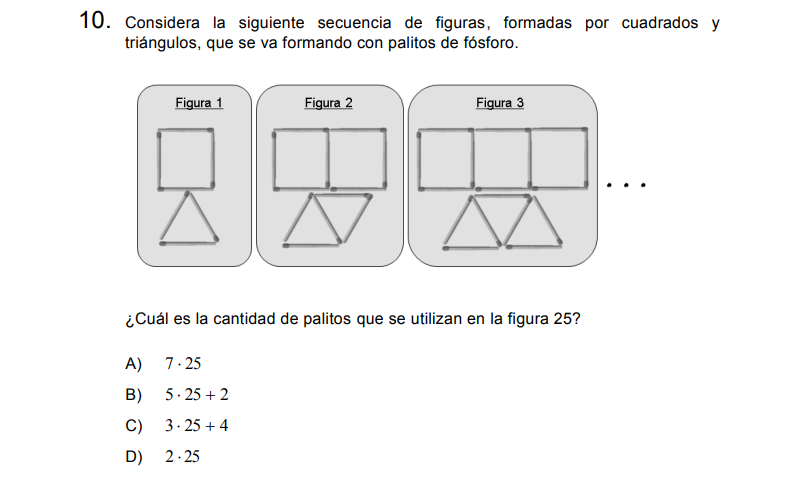
Vamos a determinar las secuencias por separado y luego sumar los palitos
Los cuadrados:
\[4, 7, 10= 4 + 3\cdot n, \text{con} \text{ } n={0,1,2,3,…}\]
Los triángulos
\[3, 5, 7= 3 + 2\cdot n, \text{con} \text{ } n={0,1,2,3,…}\]
Para la figura 25, nuestro n sería un número menos, es decir, \(n=24\), la expresión total nos quedaría
\[4+3\cdot 24 + 3+ 2 \cdot 24\]
\[7+3\cdot 24 + 2 \cdot 24\]
Podríamos factorizar y tratar de acomodar alternativa pero creo que es más rápido calcular el valor y calcular la alternativas
\[79+48=\]
\[127\]
Veamos la alternativa B
\[5\cdot 25 +2=\]
\[125+2=127\]
Esta es la correcta!
Letra B.
P11

Solución:
Siempre le digo a mis alumnos que este tipo de preguntas se puede expresar como multiplicaciones de la siguiente manera
\[\frac{20}{100}\cdot\frac{20}{100}\cdot\frac{20}{100}\cdot P= \]
cada fracción es equivalente al 20% solicitado, ahora solo queda resolver
\[\frac{1}{5}\cdot\frac{1}{5}\cdot\frac{1}{5}\cdot P= \]
\[\frac{1}{125}\cdot P= \]
\[0,008P=\]
\[0,8%P\]
Cuidado con la transformación final, recuerden que el signo de % es equivalente a dividir por 100.
Letra A.
P12

Solución:
Resolvemos mediante una proporción, lo importante es saber quién es el 100%, una pista muy grande es la palabra «de» lo que esté después por lo general será el 100%,
\[\frac{100}{125}=\frac{x}{25}\]
\[\frac{100\cdot 25}{125}=x\]
\[\frac{100\cdot 1}{5}=x\]
\[20=x\]
Letra B.
P13

Solución:
Debemos ir calculando los porcentajes de manera sucesiva
10% de 1000:
\[\frac{1}{10}\cdot 1000=100\]
100 estudiantes practican patinaje.
10% de 100
\[\frac{1}{10}\cdot 100=10\]
10 estudiantes participan en torneo.
Con esta información buscamos la alternativa correcta.
A. No es posible afirmar que el curso de Helena tiene solo 10 estudiantes.
B. Es incorrecto afirmar que el 99% no practica patinaje.
C. CORRECTA!
Letra C.
P14

Solución:
Para resolver este problema, al sueldo por jornada de trabajo normal le añadiremos un 20%, podemos calcular el 20% y sumárselo o bien incluir el 20% en el cálculo multiplicando por 1,2. Voy a realizar lo segundo:
\[28.000 \cdot 1,2= \]
\[33.600\]
Letra A.
P15

Solución:
Para resolver calcularemos primero el aumento y a ese valor procederemos a calcularle el descuento respectivo.
Aumento:
\[6.000 \cdot 1,75=\]
\[10.500\]
Descuento:
\[10.500 \cdot 0.75=\]
\[7.875\]
Letra B.
P16

Solución:
La cantidad de habitaciones disponibles son 60, calculamos el porcentaje que representan estas 60 habitaciones de las 200 con una proporción.
\[\frac{\text{%}}{habitaciones}=\frac{100}{200}=\frac{x}{60}\]
\[\frac{100}{200}=\frac{x}{60}\]
\[\frac{100\cdot 60}{200}=x\]
\[\frac{60}{2}=x\]
\[30=x\]
Letra A.
P17
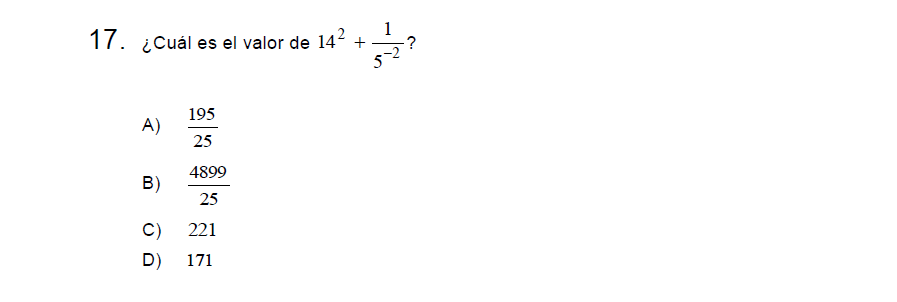
Solución:
\[14^2+\frac{1}{5^{-2}}\]
\[196+\frac{1}{5^{-2}}\]
\[196+\frac{5^2}{1}\]
\[196+\frac{5^2}{1}\]
\[196+25\]
\[221\]
Si no recuerdan propiedades de potencias, vayan a ver mi post 😉.
Letra C.
P18

Solución:
En este problema debemos descomponer el 888
\[888=\]
\[8\cdot 111=\]
\[2^3\cdot 111=\]
Sin embargo, todo está elevado a 2, por lo tanto nos queda
\[(2^3\cdot 111)^2=\]
\[2^6\cdot 111^2=\]
Letra A.
P19

Solución:
Para resolver recordemos un poco lo aprendido en básica, cuando nos enseñaron a descomponer números, por ejemplo:
\[365= 300 + 60 + 5 = 3 \cdot 100 + 6 \cdot 10 + 5 \cdot 1= 3\cdot 10^2 + 6\cdot 10^1 + 5\cdot 10^0\]
Con este ejemplo podemos analizar nuestra situación
\[mtp=m\cdot 10^2 + t \cdot 10^1 + p \cdot 10^0\]
Letra D.
P20
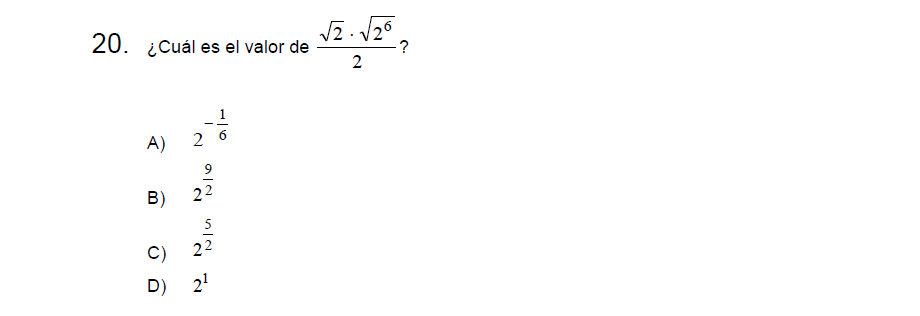
Solución:
\[\frac{\sqrt{2} \cdot \sqrt{2^6}}{2}=\]
\[\frac{2^{\frac{1}{2}}\cdot 2^{\frac{6}{2}}}{2^1}=\]
\[2^{(\frac{1}{2}+3-1)}=\]
\[2^{(\frac{1}{2}+2)}=\]
\[2^{(\frac{1}{2}+\frac{4}{2})}=\]
\[2^{\frac{5}{2}}\]
Letra C.
P21
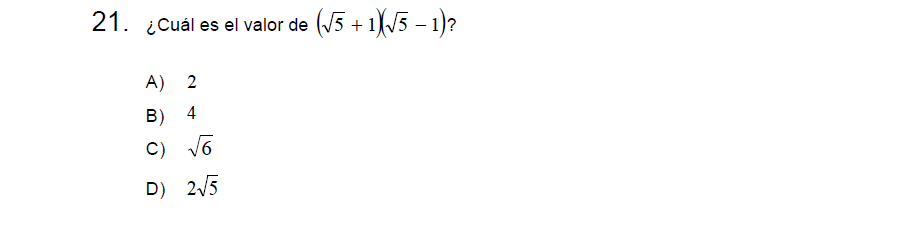
Solución:
Tenemos una suma por su diferencia, si no recuerdan productos notables vayan a ver mi post :3
\[(\sqrt{5}+1)(\sqrt{5}-1)=\]
\[(\sqrt{5})^2 – (1)^2=\]
\[5-1=4\]
Letra B.
P22

Solución:
Las dos horas equivalen a 120 minutos, es decir, el aumento ha ocurrido 3 veces, podemos ir multiplicando las cantidades por el factor 1,2, de esta manera aumentamos un 20%
\[250\cdot 1.2=25\cdot 10 \cdot 1.2 = 25\cdot 12=300\]
\[300\cdot 1.2= 120\cdot 3 = 360\]
\[360\cdot 1.2 = 36\cdot 12=432\]
Con los aumentos listos, hacemos la diferencia para determinar la cantidad de aumento
\[432 – 250=182\]
Letra C.
P23

Solución:
Para responder esta pregunta debemos dividir la cantidad de terabyte entre la cantidad de megabyte, como ambos están escritos en bytes solo transformaremos a potencia de base 10 y dividimos como potencias.
\[10^{12}:1.000.000=\]
\[10^{12}:10^6=\]
\[10^{12-6}=\]
\[10^6\]
Letra C.
P24

Solución:
Tenemos un cuadrado de binomio, si no recuerdan productos notables vayan a ver mi post :3
\[(2x-3)^2=(2x)^2-2(2x)(3)+(3)^2=\]
\[4x^2-12x+9\]
Letra C.
P25

Solución:
PASO 1: Correcto «se multiplica término a término»
PASO 2: Aquí se comete el error puesto que no se sumaron los exponentes al multiplicar las potencias de igual base, por ejemplo: \[3x\cdot x^2 = 3x^3\]
Letra B.
P26

Solución:
Voy a ir construyendo la expresión paso a paso, PEERO desde atrás
Un número x: \(x\)
El cubo de ese número: \(x^3\)
El doble del cubo de ese número: \(2x^3\)
Lo anterior disminuido: \(2x^3-\)
Un tercio del número: \(\frac{x}{3}\)
Todo junto: \(2x^3-\frac{x}{3}\)
Letra D.
P27

Solución:
Antes de reducir los términos vamos a resolver el cuadrado de binomio
\[-y-2(y-2)^2=\]
\[-y-2(y^2-4y+4)=\]
\[-y-2y^2+8y-8=\]
\[-2y^2+7y-8\]
Letra D.
P28

Solución:
Si 325 gramos de harina hacen 20 galletas, para hacer 1 sola galleta tendremos que usar \(\frac{325}{20}\), para \(n\) galletas, multiplicamos lo anterior por \(n\)
\[\frac{325}{20}\cdot n\]
Letra A.
P29
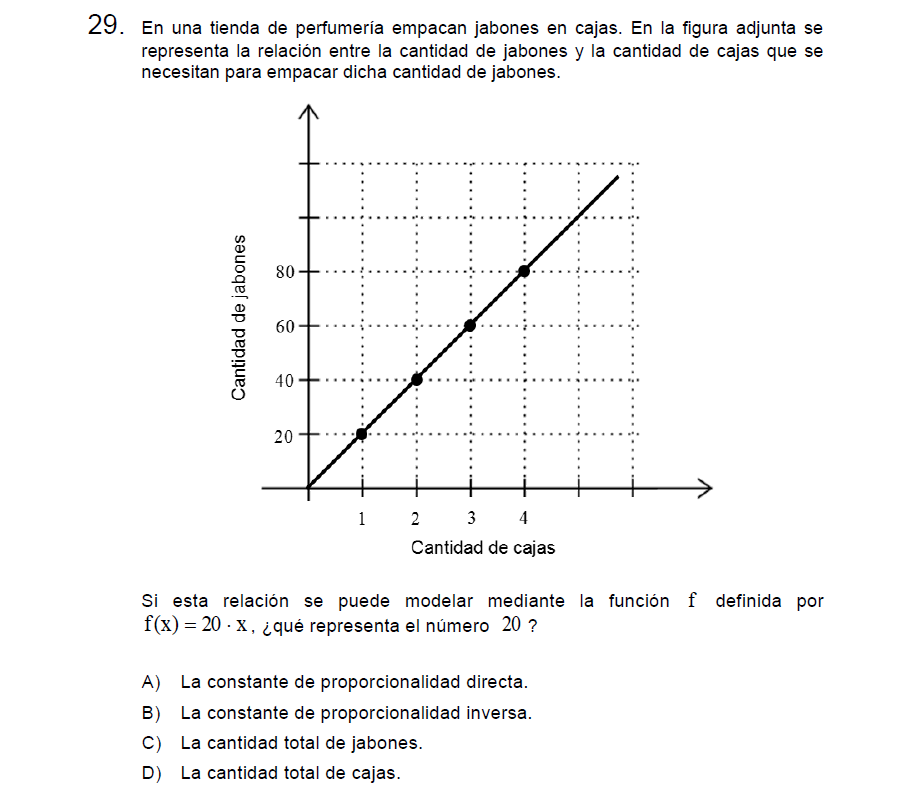
Solución:
El número 20 es la coordenada \(y\) del punto, este punto es \((1,20)\) y se puede interpretar como: «Por cada 1 caja se tienen 20 jabones». Siempre que ustedes logren reducir una expresión a «por cada 1 algo se tienen x otras cosas» han encontrado la constante de proporcionalidad directa. Es directa puesto que «si aumentamos la cantidad de cajas al doble, la cantidad de jabones también aumentaría al doble».
Letra A.
P30

Solución:
Vamos representando paso a paso, recuerden que siempre les recomendaré dar la incógnita a quién tengan menos o sea el menor. Es así que
Ariel: \(x\)
Carmen: \(x+13\)
nos faltaría transformar la frase «a lo más» esto significa como máximo, es decir, la cantidad debe ser «menor o igual a 49» \(\leq\).
La inecuación resultante sería
\[x+(x+13)\leq 49\]
\[2x+13\leq 49\]
\[2x\leq 36\]
\[x\leq 18\]
Si no recuerdan como resolver inecuaciones, pueden ir a ver mi post 😘
Letra B.
P31

Solución:
Para ambos tipos de cajas la cantidad es la misma, es decir, tenemos el peso de la caja multiplicado por la cantidad: \(Peso\cdot Cantidad = M\cdot x\), el peso total de la carga en el camión será la suma de todo esto: \(M\cdot x+ P\cdot x= (M+P)x\) (si no recuerdan factorización vayan a ver mi post)
Este peso no puede superar los 2100 kg, es decir, debe ser igual o menor a 2100 kg
\[(M+P)x\leq 2100\]
Letra A.
P32

Solución:
Antes de leer las opciones y viendo solo la imagen, podemos descartar dos regalos en cada balanza y llegar a la conclusión de que la Miel es más liviana que 1 regalo. Por lo tanto, cada regalo pesa más de 500 gramos.
Letra C.
P33
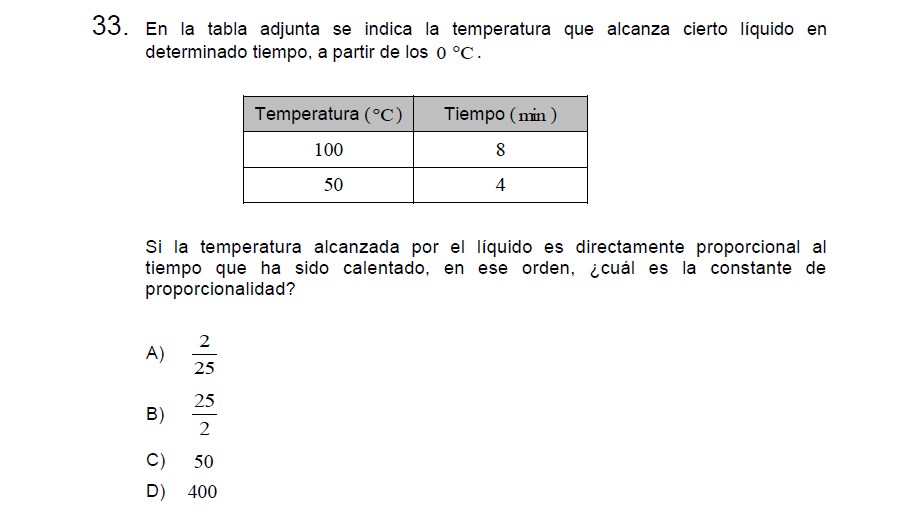
Solución:
La relación que nos presentan es
\[\text{Temperatura : Tiempo}\]
con esto en consideración podemos reemplazar un par de números y plantear la constante
\[50 : 4\]
simplificamos por 2
\[25 : 2=\frac{25}{2}\]
Letra B.
P34

Solución:
Para lograr resolver este problema, vamos a decir que \(x\) son la cantidad de bolsas que armó Raúl y que \(y\) serán las bolsas hechas por Teresa, entre los dos arman 300 bolsas, con esto tenemos la primera ecuación:
\[x+y=300\]
La segunda ecuación aparece al utilizar la siguiente información, las bolsitas de Raúl son de 3 dulces mientras que las de Teresa son de 5 dulces, además tenemos un total de 1000 dulces de los cuales no sobra ninguno, es decir:
\[3x+5y=1000\]
Con ambas ecuaciones formamos un sistema
\[x+y=300\]
\[3x+5y=1000\]
Lo pueden resolver como quieran, pero si no recuerdan como resolver sistemas de ecuaciones, ya saben que hacer (vean mi post :P).
Les recomiendo utilizar el método de reducción multiplicando la primera por -3 por ejemplo, sin embargo, por temas de edición utilizaré sustitución
Despejo la \(y\) de la primera ecuación obteniendo
\[y=300-x\]
Ahora reemplazo esta expresión en la segunda ecuación
\[3x+5(300-x)=1000\]
Resuelvo esta ecuación y tengo la respuesta al problema
\[3x+5(300-x)=1000\]
\[3x+1500-5x=1000\]
\[1500-2x=1000\]
\[-2x=-500\]
\[x=250\]
Letra A.
P35
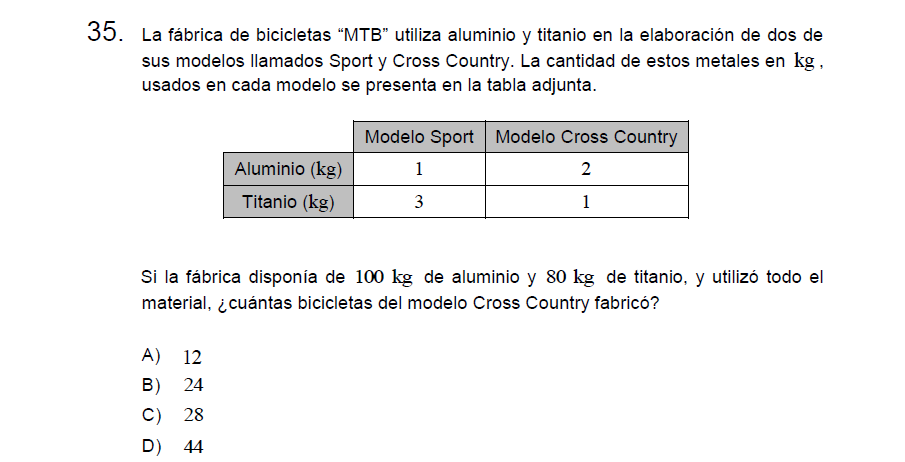
Solución:
Para resolver podemos trabajar con las alternativas
Letra A: si fueran 12 bicicletas Cross Country, se habrían usado 24 kg de Aluminio y 12 de Titanio, por lo tanto, quedan disponibles 76 kg de Aluminio y 68 de Titanio, esto implica que para gastar todo el material debieran fabricarse 76 bicicletas Sport (para gastar todo el aluminio), sin embargo, el Titanio no sería suficiente para cubrir esta cantidad. INCORRECTA!
Letra B: si fueran 24 bicicletas Cross Country, se habrían usado 48 kg de Aluminio y 24 de Titanio, por lo tanto, quedan disponibles 52 kg de Aluminio y 56 de Titanio, esto implica que para gastar todo el material debieran fabricarse 52 bicicletas Sport (para gastar todo el aluminio), sin embargo, el Titanio no sería suficiente para cubrir esta cantidad. INCORRECTA!
Letra C: si fueran 28 bicicletas Cross Country, se habrían usado 56 kg de Aluminio y 28 de Titanio, por lo tanto, quedan disponibles 44 kg de Aluminio y 52 de Titanio, esto implica que para gastar todo el material debieran fabricarse 44 bicicletas Sport (para gastar todo el aluminio), sin embargo, el Titanio no sería suficiente para cubrir esta cantidad. INCORRECTA!
Letra D: si fueran 44 bicicletas Cross Country, se habrían usado 88 kg de Aluminio y 44 de Titanio, por lo tanto, quedan disponibles 12 kg de Aluminio y 36 de Titanio, esto implica que para gastar todo el material debieran fabricarse 12 bicicletas Sport (para gastar todo el aluminio), para lo cual el Titanio, que es el triple, alcanza perfectamente. CORRECTA!
Letra D.
P36

Solución:
Nos indican que los tres segmentos pueden formar un triángulo rectángulo, con esta información podemos hacer uso del Teorema de Pitágoras, para ello debemos determinar cual es el segmento más grande, nos dan una pista importante, x no puede ser cero ni negativo, ya que no podría existir el tercer segmento si esto pasara, con esto en mente podemos determinar que x es positivo y por lo tanto \(2x+15\) es el segmento más grande
Vamos con Pitágoras
\[x^2+(2x+10)^2=(2x+15)^2\]
\[x^2+4x^2+40x+100=4x^2+60x+225\]
\[5x^2+40x+100=4x^2+60x+225\]
\[x^2+40x+100=+60x+225\]
\[x^2-20x+100=225\]
\[x^2-20x-125=0\]
Letra D.
P37

Solución:
Obtengamos los gastos por separado, es decir, con Plan y sin Plan
Con Plan:
\[Total=1000 \cdot 18+9000\cdot 6\]
\[f(18)=18.000+54.000\]
\[f(x)=72.000\]
Sin Plan:
Obtenemos el valor de la entrada con una proporción
\[\frac{Precio}{\text{%}}=\frac{1000}{20}=\frac{x}{100}\]
\[\frac{1000}{20}=\frac{x}{100}\]
\[\frac{1000}{20}\cdot 100=x\]
\[\frac{100000}{20}=x\]
\[5.000=x\]
Multiplicamos el valor por las 18 entradas
\[5.000\cdot 18 =90.000\]
Diferencia:
\[90.000-72.000=18.000\]
Letra C.
P38

Solución:
Para resolver debemos tener claro cual es el ingreso que obtenía esta persona al realizar la segunda sesión con el paciente
Sesión 1: 30.000
Sesión 2: 30.000
Con esto claro, debemos hallar la función que le otorgue un 20% de descuento en esta segunda sesión, es decir, \(30.000 + 30.000 \cdot 0.8=30.000+24.000=54.000\)
Probemos con la segunda alternativa
\[h(2)=24.000\cdot (2) +6.000 = 48.000 + 6.000 = 54.000\]
Con esa opción hemos acertado!
Letra B.
P39

Solución:
Para poder resolver esto, podríamos pensar que para disminuir un determinado Porcentaje podemos multiplicar por un factor acorde, en este caso podemos multiplicar todo por 0,75, esto equivale a disminuir un 25% el precio
\[300x+500\]
\[(300x+500)\cdot 0,75=\]
\[300x\cdot 0,75+500\cdot 0,75=\]
\[225x+375\]
Letra C.
P40

Solución:
Vamos a evaluar (reemplazar el valor que nos dan en el paréntesis en la función f(n)) todas las funciones y luego resolver
\[f(1)=10+25n-5n^2=10+25\cdot 1-5(1)^2=10+25-5=30\]
\[f(2)=10+25n-5n^2=10+25\cdot 2-5(2)^2=10+50-20=40\]
\[f(3)=10+25n-5n^2=10+25\cdot 3-5(3)^2=10+75-45=40\]
\[f(4)=10+25n-5n^2=10+25\cdot 4-5(4)^2=10+100-80=30\]
Sumamos
\[30+40+40+30=140\]
Letra B.
P41
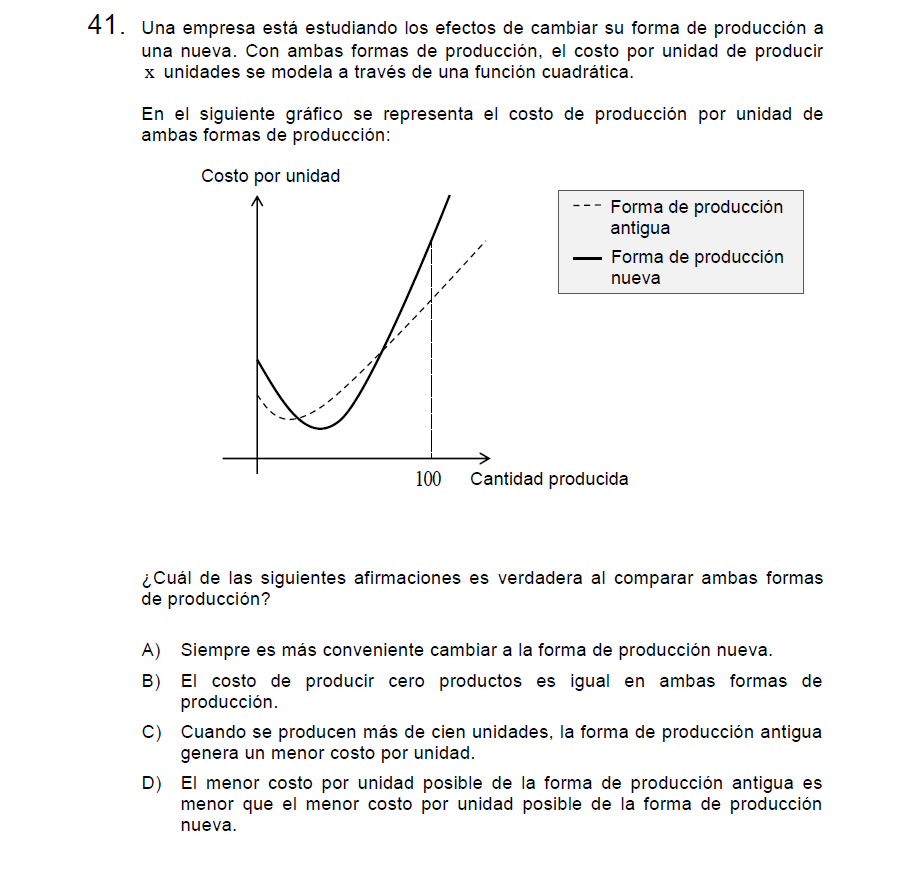
Solución:
Veamos una a una y recuerden que si quieren recordar más acerca de Función Cuadrática pueden ver mi post 🔥.
Letra A: Claramente No es así ya que por ejemplo, para 100 Productos el costo es más elevado, se ve reflejado en que su grafica (línea negra continua) está «más arriba».
Letra B: Falos nuevamente la forma nueva de producción inicia «más arriba», es más costosa.
Letra C: Esto es CORRECTO, lo había comentado en la Letra A.
Letra D: Esto es Falso, la nueva forma de producción tiene un mínimo más económico.
Letra C.
P42

Solución:
Veamos una a una
Letra A: 0,75 está a la mitad de 0,5 y 1 por lo tanto visualmente podemos deducir que la coordenada \(Y\) en este valor de \(X\) no corresponde, sino que es un poco más.
Letra B: Al estar en 1 segundo llegamos al punto más alto de la parábola, su máximo (40 cm). CORRECTO.
Letra C: A los 1,5 la altura es menor de 30 cm.
Letra D: Esto no es posible de verificar, sin embargo, entendemos que el grillo solo aterriza en el suelo ya que estamos en una situación contextualizada a la «normalidad».
Letra B.
P43
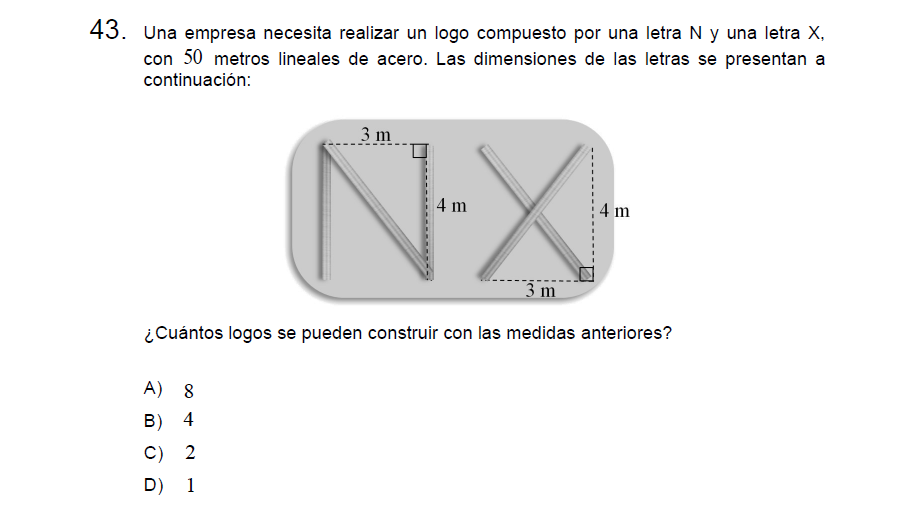
Solución:
Utilizando Pitágoras podemos obtener las medidas de los segmentos diagonales (hipotenusas), es un trío pitagórico por lo cual mide 5, de todas maneras puedo calcularlo para ustedes
\[3^2+4^2=x^2\]
\[9+16=x^2\]
\[25=x^2\]
\[5=x\]
Para hacer la N, necesitamos \(4+4+5=13\) metros.
Para hacer la X, necesitamos \(5+5=10\) metros.
Ambas letras suman \(23\) metros y como solamente disponemos de 50 metros, podemos construir dos logos \(23+23=46\).
Letra C.
P44

Solución:
La condición dada es la clave para resolver, si nos piden mantener perpendicular el asiento, nos están pidiendo un triángulo rectángulo, de este modo, es Pitágoras quién nos ayudará nuevamente. Nos piden determinar la distancia desde A hasta B, en otras palabras, la expresión que permita calcular la hipotenusa.
\[D_{AB}^2=AO^2+BO^2\]
\[D_{AB}=\sqrt{AO^2+BO^2}\]
Letra B.
P45
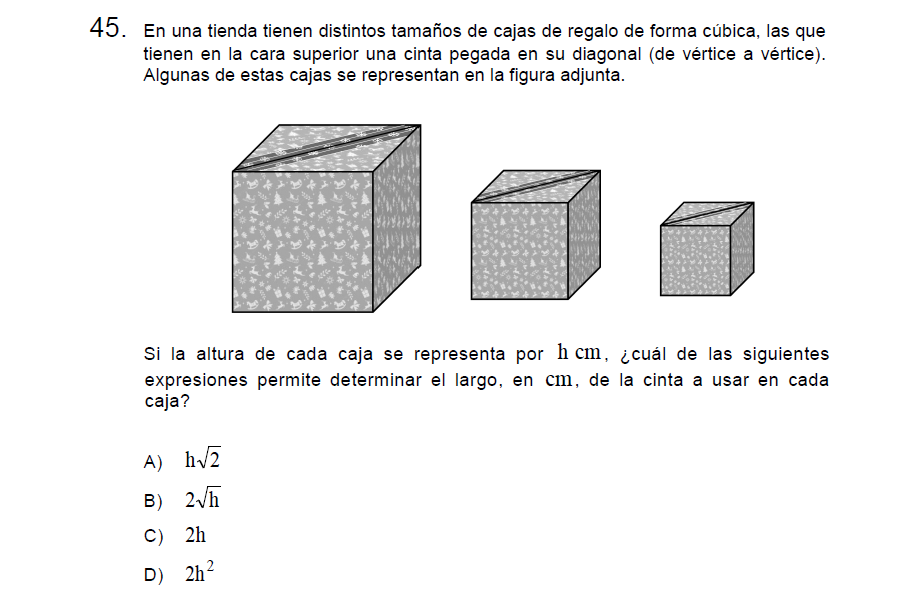
Solución:
Nos están pidiendo determinar la diagonal de un cuadrado, para esto pueden aprender la formula de memoria que es «lado multiplicado por raíz de 2», de todas maneras lo calcularé para ustedes.
Como es un cubo, las aristas miden todas \(h\), utilizando Pitágoras tenemos
\[x^2=h^2+h^2\]
\[x^2=2h^2\]
\[x=\sqrt{2h^2}\]
\[x=h\sqrt{2}\]
Letra A.
P46

Solución:
Calculemos primeramente el área (\(\pi r^2\)) de la circunferencia P
\[A_P=\pi\cdot 3^2=9\pi\]
EL área de Q es un cuarto de esto, es decir,
\[A_Q=\frac{1}{4}\cdot 9\pi\]
Utilizando la fórmula del área lograremos encontrar la medida del radio
\[A_Q=\pi\cdot r^2\]
\[\frac{1}{4}\cdot 9\pi=\pi\cdot r^2\]
se cancelan los \(\pi\)
\[\frac{1}{4}\cdot 9=r^2\]
\[\frac{9}{4}=r^2\]
\[\sqrt{\frac{9}{4}}=r\]
\[\frac{3}{2}=r\]
Letra C.
P47

Solución:
Vamos viendo, la imagen es un distractor, la forma no nos interesa, necesitamos recordar la fórmula del volumen (casi siempre, área de la base por la altura) \(V=\pi \cdot r^2 \cdot h\), nuestra incógnita es la altura (\(h\)), me falta solo clarificar que «la capacidad máxima» es el dato que usamos para reemplazar por el volumen (\(V\))
\[V=\pi \cdot r^2 \cdot h\]
\[600=3 \cdot 4^2 \cdot h\]
\[600=3\cdot 16 \cdot h\]
\[600=48 \cdot h\]
\[\frac{600}{48}= h\]
\[12,5=h\]
Letra B.
P48

Solución:
Veamos esto como una caja, tenemos cuatro caras laterales rectangulares de igual área y una cara cuadrada,
El techo cuadrado es muy sencillo, \((2x)^2=4x^2\)
Ahora vamos con una cara lateral, \(2^3x\cdot 2x=8x\cdot 2x=16x^2\)
No olvidemos que son 4 caras laterales, \(4\cdot 16x^2=64x^2\)
Si sumamos todo nos queda
\[4x^2+64x^2=68x^2\]
Letra C.
P49

Solución:
Vamos a reemplazar los datos, recordando que para sumar vectores, debemos hacerlo componente a componente (x con x e y con y), nos quedaría
\[(2,-1)+(-3,2)+(a,b)+(4,3)=(6,5)\]
separamos en dos ecuaciones
\[2+(-3)+a+4=6\]
\[-1+2+b+3=5\]
Voy a resolver la primera
\[a+3=6\]
\[a=3\]
Voy con la segunda
\[-1+2+b+3=5\]
\[b+4=5\]
\[b=1\]
Letra C.
P50
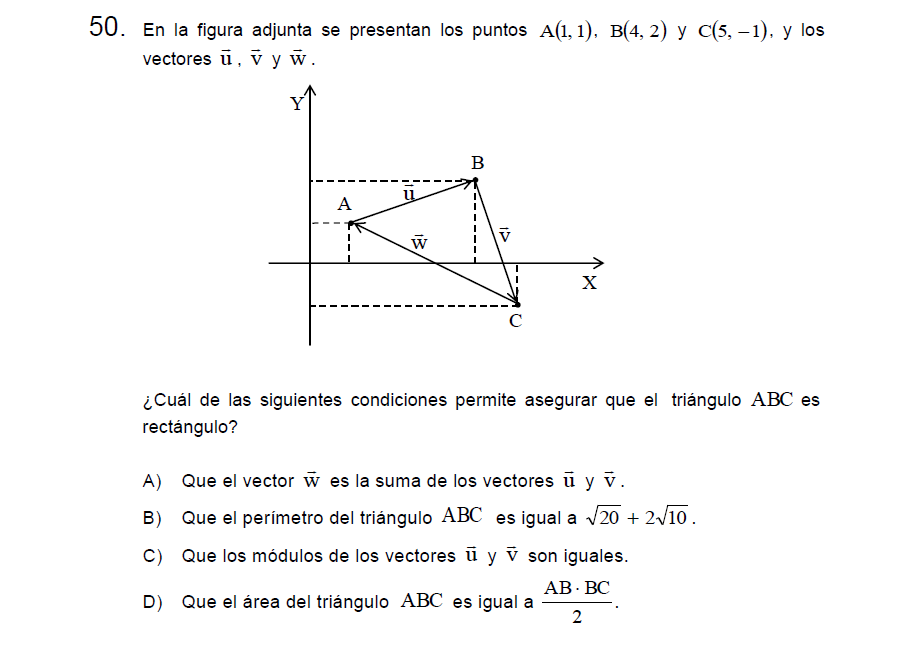
Solución:
Vamos viendo,
Letra A: Si pudiéramos formar una relación como con Pitágoras esto tendría sentido, es decir, si la suma de los cuadrados de los módulos fueran igual al cuadrado de w, sin embargo no es suficiente.
Letra B: En este caso se han calculado los valores de los módulos, sin embargo, no implica que sea rectángulo.
Letra C: Esto nos origina un triángulo isósceles no necesariamente rectángulo.
Letra D: Es la correcta puesto que el área de un triángulo se calcula multiplicando su base por su altura, al ser altura forma un ángulo de 90°, o también recordar que esta fórmula ocurre de manera directa en un triángulo rectángulo.
Letra D.
P51

Solución:
Vamos entendiendo los datos, si está en el primer cuadrante ambas coordenadas son positivas y si está en el tercero, ambas son negativas.
En el primer caso al ser reflejado respecto al eje Y, la coordenada x queda negativa.
En el segundo caso al ser reflejado respecto al eje Y, la coordenada x queda positiva.
La verdad es que en ambos casos no importa donde quede ya que si hablamos de distancia, esta es positiva, luego pensemos en que el punto inicial era (2,3) y al ser reflejado queda en el (-2,3), la distancia entre ambos puntos es de 4 unidades, el doble de la coordenada x.
Letra C.
P52

Solución:
Revisemos Paso a Paso
Paso 1: \((-5+5,5-2)=(0,3)\), UPS! aquí está el error, genial!
Letra A.
P53
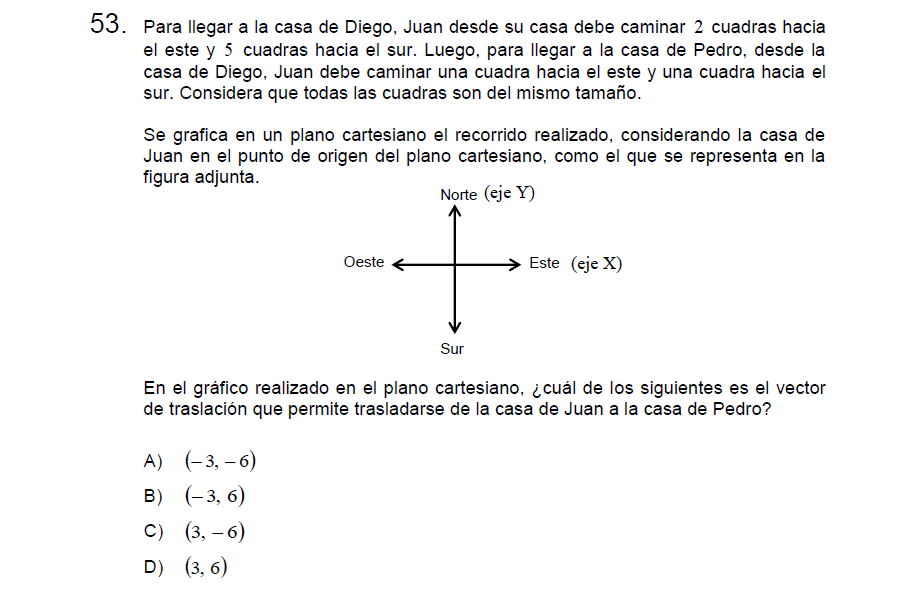
Solución:
Para resolver escribiremos los vectores descritos y luego los uniremos en uno solo
De Juan a Diego:
\[(2,-5)\]
Ahora de Diego a Pedro:
\[(1,-1)\]
Unamos ambos (sumamos ambos vectores, componente a componente 2+1 y -5+-1)
\[(3,-6)\]
Letra C.
P54
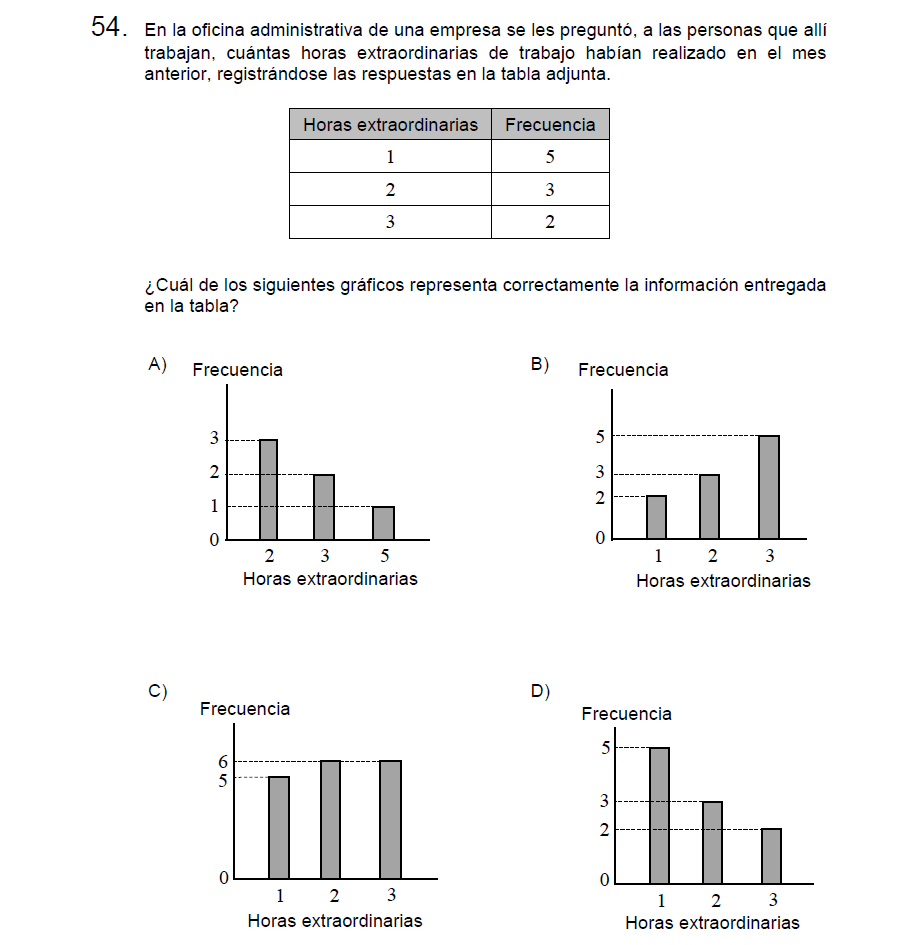
Solución:
Veamos los errores 1 a 1,
Letra A: Están intercambiados los valores de Frecuencia y Horas.
Letra B: Quienes han realizado 1 hora extraordinaria son 5 personas, el gráfico dice 2.
Letra C: Dice que quienes han realizado 2 horas extraordinarias son 6 personas, lo correcta era 3.
Letra D: Correcta!
Letra D.
P55
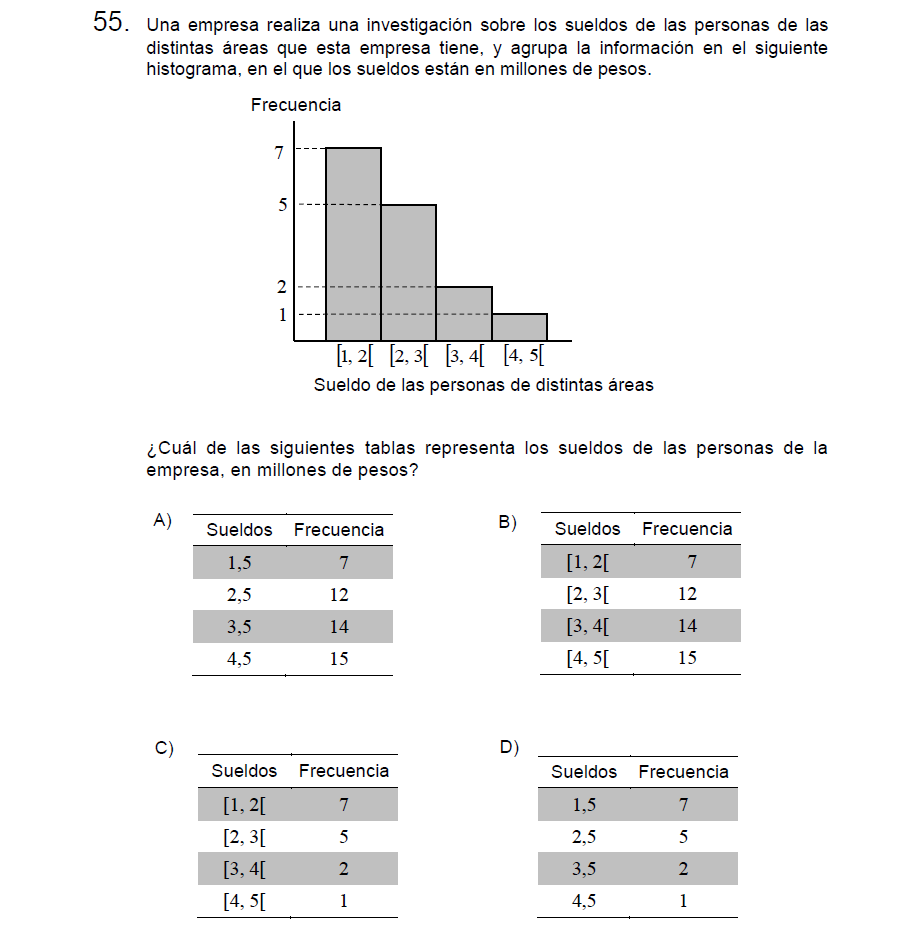
Solución:
Podemos descartar A y B, puesto que en la segunda fila (de 2 a 3 millones) debiera decir.
Descartamos D porque señala las marcas de clase de los intervalos y no los intervalos.
Letra C.
P56

Solución:
Vamos descartando
Letra A: El rango es la diferencia entre el mayor y el menor dato, es decir, \(16-6=10\). FALSA
Letra B: Calculemos el promedio
\[\frac{12+6+14+12+16}{5}=\frac{60}{5}=12\] VERDADERA
Letra C: Ordenamos los datos {6, 12, 12, 14, 16}, la mediana es 12. FALSA
Letra D: La moda es 12.
Letra B.
P57

Solución:
Antes de calcular el promedio, añadimos las nuevas ventas
P1: \(120+80=200\)
P2: \(200+80=280\)
P3: \(200+100=300\)
P4: \(250+40=290\)
Como todos los productos fueron vendidos durante el mismo tiempo, basta con ver cual vendió más para saber la respuesta (tendrá también el mayor promedio).
Letra C.
P58
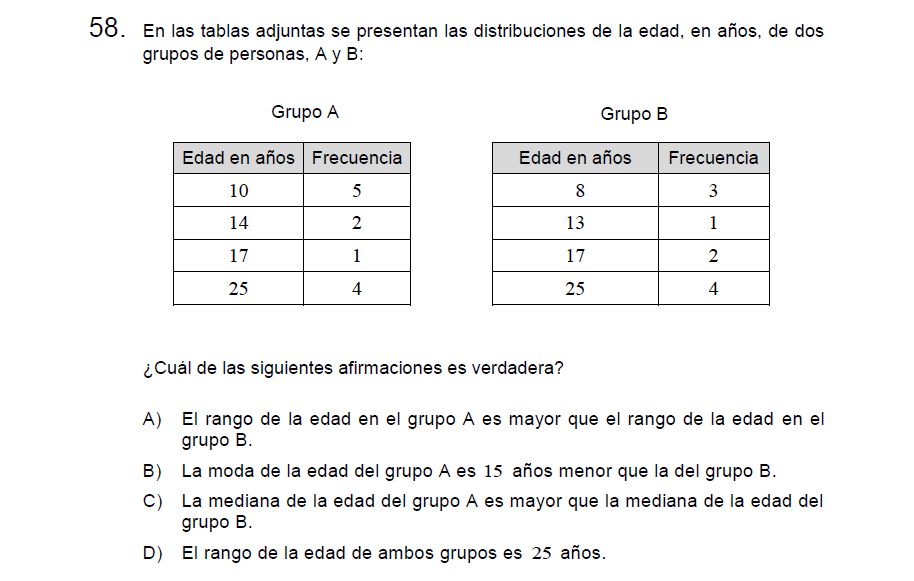
Solución:
Probemos nuevamente una a una
Letra A: Rango grupo A: \(25-10=15\), Rango grupo B: \(25-8=17\). FALSA
Letra B: Moda grupo A: 10, Moda grupo B: 25. VERDADERA
Letra B.
P59

Solución:
Para el promedio, sumamos todos los datos y dividimos entre 12
\[\text{promedio}=\frac{4+1+1+0+3+2+2+3+0+1+1+6}{12}=\frac{24}{12}=2\]
Letra B.
P60

Solución:
Analicemos cada aun
Letra A: Esta persona podría pertenecer al 40% que no entra en la categoría
Letra B: Esto es correcto, ya que el percentil 40 debería ser igual o menor al 60% de menores ingresos.
Letra B.
P61
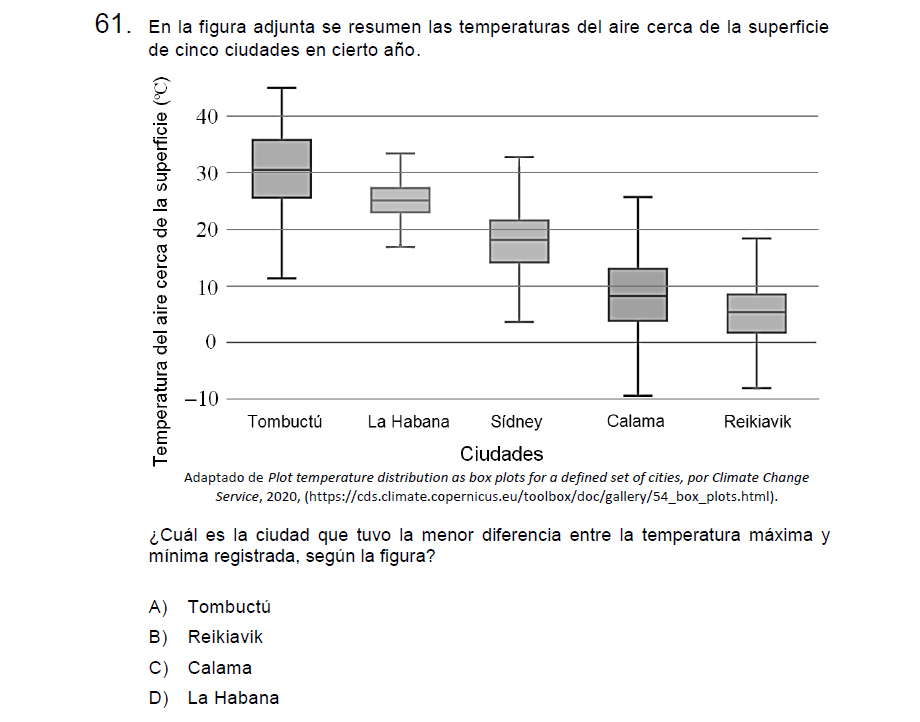
Solución:
Para responder esta pregunta debemos fijarnos en lo largo de los bigotes de nuestra caja y lo ancha que sea la caja, La Habana resulta ser la «más compacta» por lo tanto presenta menor variabilidad entre sus temperaturas.
Letra D.
P62

Solución:
Tenemos 12 datos los cuales ya están ordenados de menor a mayor, procedemos a calcular los percentiles solicitados, recomiendo iniciar con el percentil más alto, debiera ser la respuesta correcta, veamos
\[P_{40}=\frac{40}{100}\cdot 12=4,8\]
El percentil 40 se ubica entre los datos 4 y 5, más próximo al dato 5, es decir al 101.
Comprobemos calculando el percentil 30
\[P_{30}=\frac{30}{100}\cdot 12=3,6\]
Este percentil se ubica entre el dato 3 y 4, por lo tanto no supera los 98 g.
Si no recuerdan como obtener los Percentiles, ya saben donde ir (a mi post obvio :3)
Letra D.
P63

Solución:
Para resolver podemos hacer la combinación de los pares que cumplen la condición dada
Suma Para: \({(1,7),(1,9),(2,6),(2,8),(2,10),(3,7),(3,9),(4,6),(4,8),(4,10),(5,7),(5,9)}\)
Son en total 12 combinaciones favorables, nos falta determinar el total de combinaciones, para ello multiplicamos las opciones de cada caja, es decir, 5×5=25.
La probabilidad quedaría
\[\frac{12}{25}\]
Letra C.
P64

Solución:
Con las condiciones dadas en el problema tenemos que en total asisten \(6+10+3+x=19+x\). Se nos solicita la probabilidad de que la persona hable español (casos favorables), es decir, los 3 que hablan todos los idiomas más los «x», la probabilidad nos quedaría
\[\frac{x+3}{19+x}\]
Letra D.
P65

Solución:
Realizaremos el proceso inverso en este caso, plantearemos la probabilidad otorgada y la amplificaremos para que coincida con los valores dados, es decir, para que el 50 se transforme en 250
\[\frac{1}{50}\cdot \frac{5}{5}=\frac{5}{250}\]
Esto significa que compró 5 números de la rifa
Letra B.
