Sistemas de ecuaciones lineales con 2 incógnitas

Aprender a resolver sistemas de ecuaciones lineales con 2 incógnitas es fundamental en el estudio del álgebra. Estos sistemas, compuestos por dos ecuaciones con dos variables, tienen múltiples aplicaciones en la vida cotidiana y en diversas disciplinas científicas.

¿Qué es un sistema de ecuaciones lineales?

Un sistema de ecuaciones lineales es un conjunto de dos o más ecuaciones lineales con las mismas incógnitas. La solución de un sistema es el conjunto de valores que satisfacen simultáneamente todas las ecuaciones.  

Imagina que tienes dos rompecabezas y cada pieza representa una incógnita. Resolver un sistema de ecuaciones lineales con dos incógnitas es como encontrar las piezas exactas que encajan en ambos rompecabezas al mismo tiempo. Es como descifrar un código secreto con dos claves, donde ambas deben funcionar juntas para revelar la solución.

Los sistemas de ecuaciones lineales son como las balanzas de una tienda de abarrotes. Cada ecuación representa una balanza en equilibrio, donde los pesos de cada lado deben ser iguales. Al resolver el sistema, estamos ajustando los pesos hasta encontrar el punto exacto donde ambas balanzas están perfectamente niveladas.

Desde calcular la cantidad de ingredientes para una receta hasta determinar la velocidad y dirección de un avión, estos sistemas son herramientas poderosas para modelar y resolver problemas. Por ejemplo, un economista podría usar sistemas de ecuaciones para analizar la relación entre la oferta y la demanda de un producto. Un ingeniero civil podría utilizarlos para calcular las fuerzas que actúan sobre una estructura. Nos permiten modelar situaciones reales de forma matemática y encontrar soluciones precisas. Además, son la base para el estudio de temas más avanzados en matemáticas, como el álgebra lineal y el cálculo.

Exploraremos los diferentes métodos para resolver sistemas de ecuaciones lineales con dos incógnitas. Veremos el paso a paso a través de cada método, proporcionándote ejemplos claros y concisos. Al finalizar, serás capaz de resolver cualquier sistema de ecuaciones lineales con confianza.

Paso a paso

Entendamos que significa resolver un sistema de ecuaciones. Como toda ecuación intentamos encontrar el valor de una incógnita, en nuestro caso 2 incógnitas, pero además, podemos entender este tipo de ecuaciones como Rectas!, rectas que queremos determinar si se interceptan (cruzan) o no, en este sentido, el resultado sería el PUNTO donde se interceptan las rectas.

Ejemplo:

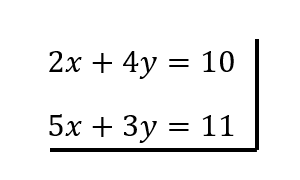
Como pueden ver tenemos dos ecuaciones con dos incógnitas cada una (x e y), además ninguna de ellas está elevada a 2 u otro exponente.

Es importante en cada ejercicio ordenar las ecuaciones, en nuestro buen chileno, pasando de un lado a otro las incógnitas y los números, de tal manera que las incógnitas queden a la izquierda y los números a la derecha.

Método Gráfico

El método gráfico consiste en Graficar!, graficamos ambas rectas y luego vemos en que punto se interceptan.

Para graficar podemos apoyarnos de una tabla como la siguiente

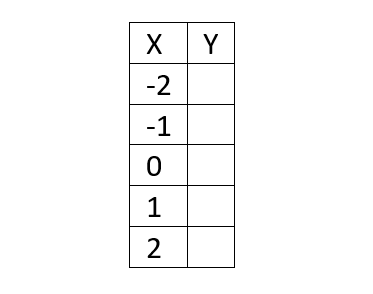
Los valores de X los damos nosotros, yo aconsejo dar valores cercanos al centro del plano cartesiano por eso incorporo el 0 y valores cercanos a él, sin embargo, con solo dos puntos basta para graficar.

Los valores de Y son el resultado de evaluar (reemplazar) el valor de X.

Sigamos con el ejemplo anterior

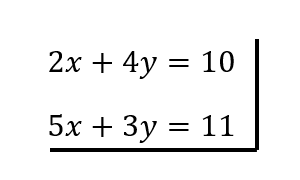
Completaremos la tabla para la primera ecuación, ya que es el mismo proceso para la segunda

Despejamos \(y\) y reemplazamos

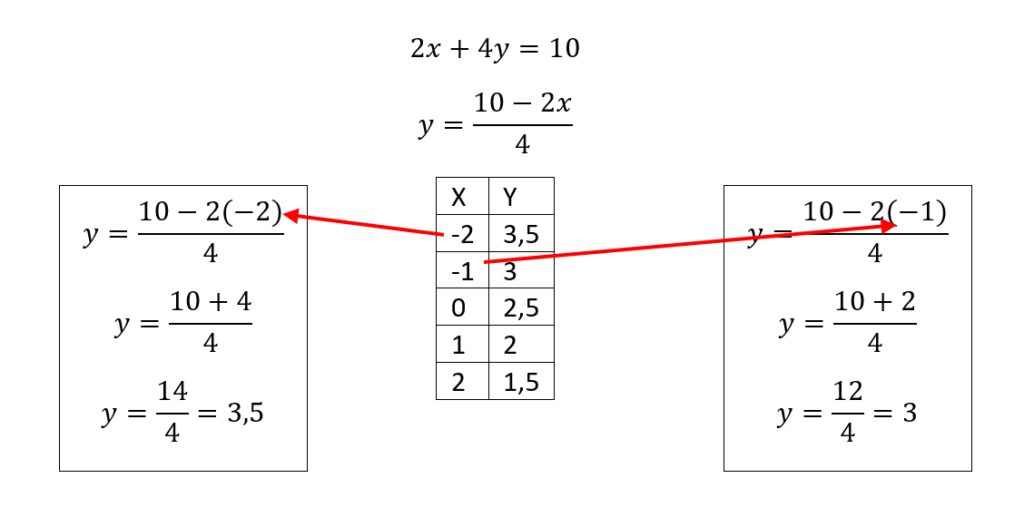
Con todos estos puntos en la tabla podemos graficar, aprovecharé de incluir la otra recta también

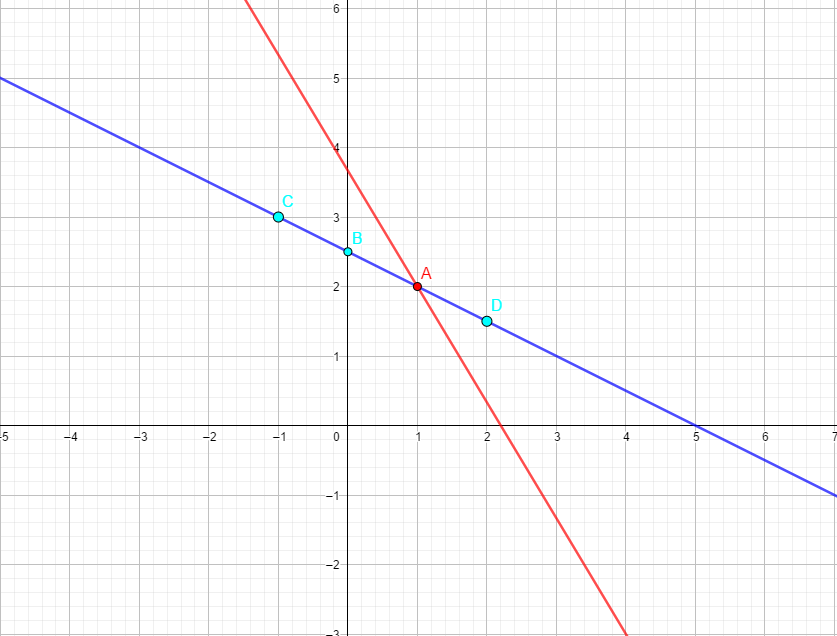
El punto A es donde se interceptan ambas y la solución de este sistema, el punto (1,2).

Claramente este método no es el más rápido, veamos los siguientes.

Método de Reducción

Seguiremos apoyándonos en el sistema anterior,

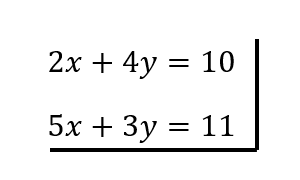
Voy a dejarles los pasos a seguir para resolver el sistema utilizando este método:

1. Elegir una de las dos incógnitas
2. Multiplicar las ecuaciones para que los coeficientes se igualen pero con signos contrarios
3. Sumar ambas ecuaciones
4. Resolver la ecuación resultante
5. Reemplazar el valor encontrado para determinar la otra incógnita

Pongamos en práctica estos pasos

Vamos a elegir la \(x\), por nada en especial, aunque siempre les recomendaré elegir aquella que les parezca más fácil.

Los coeficientes de la \(x\) son 2 y 5

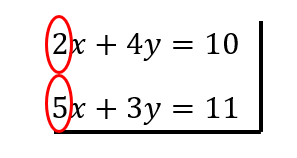
por lo tanto, debemos pensar en «por cuánto multiplico ambas ecuaciones para que se igualen los números», aquí alguien puede decir, aaaa pero pensemos en el MCM (mínimo común múltiplo) y tiene razón, entre 2 y 5, es el número 10, por lo tanto, respondemos la pregunta, ¿por cuánto multiplico el 2 y el 5 para que me de 10?

EXACTO!, multiplicamos por 5 y por 2 respectivamente, lo único importante a recordar, es que uno de los dos sea negativo para que nos queden signos contrarios (-2), nos quedará algo como

Ahora que los coeficientes están «igualados», sumamos hacia abajo

\[0x+14y=28\]

\[14y=28\]

\[y=\frac{28}{14}\]

\[y=2\]

Hemos obtenido el valor de una incógnita, con esto podemos obtener la otra. Para hacerlo vamos a reemplazar en cualquiera de las ecuaciones iniciales, por ejemplo en \(2x+4y=10\)

\[2x+4y=10\]

\[2x+4(2)=10\]

\[2x+8=10\]

\[2x=2\]

\[x=1\]

\[S=(1,2)\]

Este último paso se repite en todos los métodos que siguen.

Método de Igualación

Seguiremos apoyándonos en el sistema anterior,

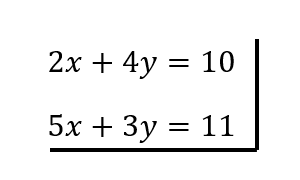
Voy a dejarles los pasos a seguir para resolver el sistema utilizando este método:

1. Elegir una de las dos incógnitas
2. Despejar esa incógnita en ambas ecuaciones
3. Igualar las expresiones
4. Resolver la ecuación resultante
5. Reemplazar el valor encontrado para determinar la otra incógnita

Pongamos en práctica estos pasos

Trabajaremos con \(y\), procedamos a despejar en ambas ecuaciones

\[2x+4y=10\]

\[4y=10-2x\]

\[y=\frac{10-2x}{4}\]

Lista la primera, vamos con la segunda

\[5x+3y=11\]

\[3y=11-5x\]

\[y=\frac{11-5x}{3}\]

Lista la segunda, ahora igualamos ambas expresiones

\[\frac{10-2x}{4}=\frac{11-5x}{3}\]

\[3(10-2x)=4(11-5x)\]

\[30-6x=44-20x\]

\[20x-6x=44-30\]

\[14x=14\]

\[x=1\]

Con esta incógnita lista podemos obtener la otra, reemplazamos en cualquier ecuación inicial, recomiendo hacerlo en aquellas que ya despejamos, por ejemplo:

\[y=\frac{11-5x}{3}\]

\[y=\frac{11-5(1)}{3}\]

\[y=\frac{11-5}{3}\]

\[y=\frac{6}{3}\]

\[y=2\]

\[S=(1,2)\]

Listo, vamos por el último método que estudiaremos en este post!!

Método de sustitución

Seguiremos apoyándonos en el sistema anterior,

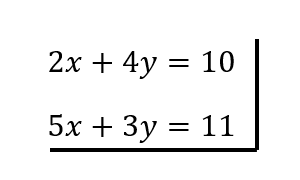
Voy a dejarles los pasos a seguir para resolver el sistema utilizando este método:

1. Elegir una de las dos incógnitas
2. Despejar esa incógnita en una ecuación
3. Reemplazar esta expresión en la otra ecuación
4. Resolver la ecuación resultante
5. Reemplazar el valor encontrado para determinar la otra incógnita

Pongamos en práctica estos pasos

Trabajaremos con \(x\) y vamos a despejar en la primera ecuación, por nada en especial, solo por mantener un orden

\[2x+4y=10\]

\[2x=10-4y\]

\[x=\frac{10-4y}{2}\]

Ahora reemplazamos esta expresión en la segunda ecuación

\[5x+3y=11\]

\[5(\frac{10-4y}{2})+3y=11\]

Resolvemos

\[5(\frac{10-4y}{2})+3y=11\]

\[5(\frac{10-4y}{2})=11-3y\]

\[5(10-4y)=2(11-3y)\]

\[50-20y=22-6y\]

\[50-22=20y-6y\]

\[28=14y\]

\[2=y\]

Con este valor listo obtenemos el otro, reemplazamos en cualquier ecuación, sin embargo, recomiendo hacerlo en la que ya está despejada

\[x=\frac{10-4y}{2}\]

\[x=\frac{10-4(2)}{2}\]

\[x=\frac{10-8}{2}\]

\[x=\frac{2}{2}\]

\[x=1\]

\[S=(1,2)\]

Problemas con enunciados

1. Un cuarto de la suma de dos números es 152 y un tercio de su diferencia es 66. ¿Cuáles son los números?
Solución:

Planteamos la primera ecuación utilizando: «Un cuarto de la suma de dos números es 152»

\[\frac{1}{4}(x+y)=152\]

Planteamos la segunda ecuación utilizando: «un tercio de su diferencia es 66.»

\[\frac{1}{3}(x-y)=66\]

Nos resulta el sistema

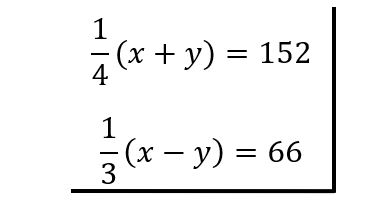
Si amplificamos las ecuaciones podemos obtener

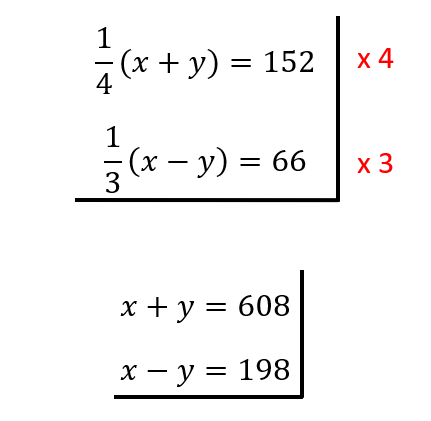
Ahora pueden resolver con cualquier método, les sugiero reducción y que simplemente sumen hacia abajo, se eliminarán las \(y\), quedando solo x, el resultado final será:

\[(403,205)\]

2. Sergio tiene $ 1.950 en monedas de $ 100 y de $ 50. En total tiene 24 monedas. Determine cuántas son de $ 100 y cuántas de $ 50.

Solución:

Al igual que en el anterior les ayudaré a plantear el sistema, pero deberán resolverlo ustedes.

Planteamos la primera ecuación usando: «En total tiene 24 monedas y son de $100 y $50.» Es decir, tiene dos tipos de monedas, la cantidad de monedas de 100 será x y la cantidad de monedas de 50 será y

\[x+y=24\]

Planteamos la segunda ecuación usando: «Sergio tiene $ 1.950 en monedas de $ 100 y de $ 50.»

\[100x+50y=1950\]

Nos queda el sistema

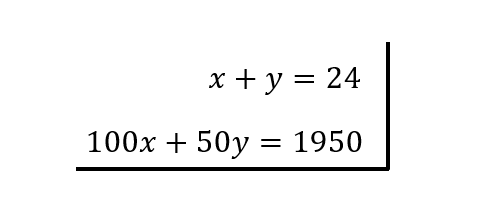
Pueden resolver con el método que prefieran, la respuesta será

\[(15,9)\]

Es decir, 15 monedas de 100 y 9 de 50.

3. Hace 5 años la edad de Manuel era 9 veces la edad de Marcos. En 5 años más la edad de Manuel será 4 veces la edad de Marcos. ¿Cuál es la edad actual de cada uno?

Solución:

Planteamos la primera ecuación usando: «Hace 5 años la edad de Manuel era 9 veces la edad de Marcos». Antes de escribirla definiremos que:

Edad de Manuel actual es: X

Edad de Marcos actual es: Y

Ahora sí

Hace 5 años tendríamos:

Edad de Manuel: \(x-5\)

Edad de Marcos: \(y-5\)

Uniendo todo nos queda

\[x-5=9(y-5)\]

Para la segunda ecuación, utilizamos «En 5 años más la edad de Manuel será 4 veces la edad de Marcos.»

En 5 años más tendríamos:

Edad de Manuel: \(x+5\)

Edad de Marcos: \(y+5\)

Uniendo todo nos queda

\[x+5=4(y+5)\]

Ojo que queremos mantener las igualdades, es por esto que siempre multiplico al menor para alcanzar la edad del mayor. El sistema definitivo es

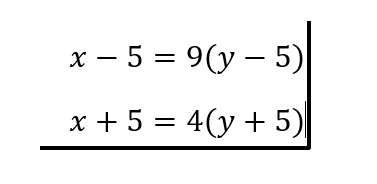
Si lo acomodamos quedaría

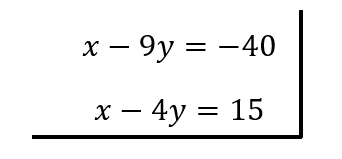
Si lo resuelven obtendrán que

\[(59,11)\]

Es decir, Manuel tiene actualmente 59 años y Marcos tiene actualmente 11 años. Pueden comprobar que se cumplen todas las condiciones en el pasado y futuro.

Espero que les sea de utilidad!, saludos!!

Video Explicativo

Adicionalmente les dejo un video de mi canal de Youtube (Profesteban), si quieren escuchar mi linda voz, se los dejo: