Función Cuadrática

La función cuadrática pudiera ser el  contenido, relacionado con funciones, que más preguntas abarca en la PAES, por lo cuál aprenderlo es de mucha importancia.

Una función cuadrática es una relación matemática entre dos variables donde una de ellas, la variable independiente, está elevada al cuadrado. Este tipo de funciones se representan algebraicamente como:

f(x) = ax² + bx + c

donde:

• a, b y c son números reales, y a es diferente de cero.
• x es la variable independiente.
• f(x) es la variable dependiente, y representa el valor de la función para cada valor de x.

¿Por qué son importantes las funciones cuadráticas? Las funciones cuadráticas tienen una amplia variedad de aplicaciones en diversos campos, como:

• Física: Describen el movimiento de proyectiles, la trayectoria de objetos lanzados al aire y la forma de cables suspendidos entre dos puntos.
• Ingeniería: Se utilizan en el diseño de estructuras, como puentes y edificios, para calcular fuerzas y deformaciones.
• Economía: Modelan fenómenos como la oferta y la demanda, el crecimiento de poblaciones y la optimización de beneficios.

Las funciones cuadráticas están presentes en diversos aspectos de la vida. En el deporte, describen la trayectoria de un penal; en la arquitectura, ayudan a diseñar los arcos del puente Chacao y las cúpulas de edificios emblemáticos en Santiago; en la economía, predicen el crecimiento de pequeñas empresas y en la naturaleza, representan la forma de las cascadas de nuestros hermosos parques nacionales y el vuelo de los cóndores. 

Las preguntas relacionadas con la función cuadrática no suelen ser muy complicadas, sin embargo, requieren que memorices varios conceptos propios de ella. A continuación, revisaremos cada uno de ellos.

1. Forma general

La forma general de la función cuadrática es:
\[f(x)=ax^2+bx+c, a≠0\]

Esta función es muy fácil de reconocer en un gráfico ya que tiene la forma de una U. ya sea hacia arriba o hacia abajo.

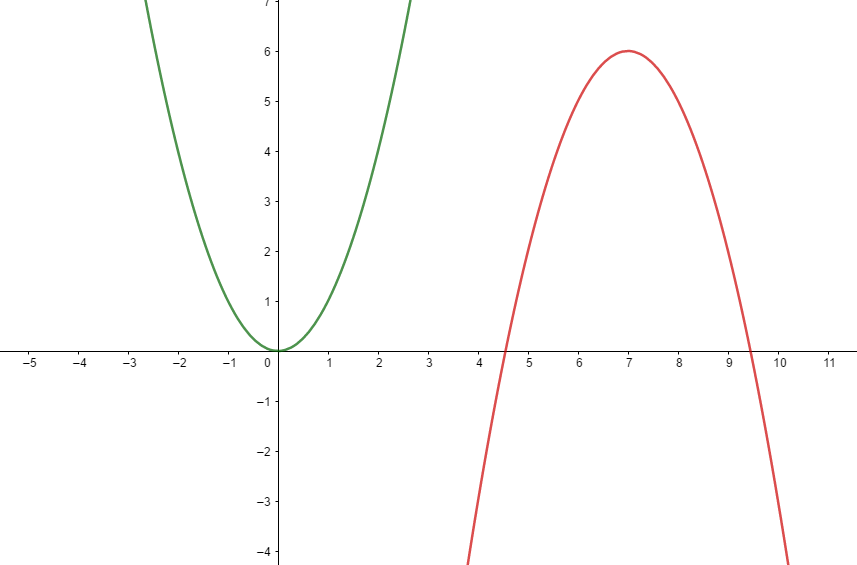
Es importante que seas capaz de reconocer en todo momento los coeficientes \( a, b \) y \(c\) ya que ellos son cruciales al determinar la concavidad, intercepciones, vértice, etc. En este sentido debes recordar que:

• \(a\) siempre acompaña a \( x^2 \)
• \(b\) siempre acompaña a \(x\)
• \(c\) es el término que no tiene \(x\)

Veamos un ejemplo rápido.

Determinar los coeficientes \(a\), \(b\) y \(c\) de la función \(f(x)=-5x+3x^2-7\).

La función está un poco desordenada, por lo cual podemos ordenarla y luego identificar los coeficientes, o bien, si eres cuidadoso(a) y recuerdas lo que acabo de decir (XD), puedes descubrirlo inmediatamente. Entonces:

\[f(x)=-5x+3x^2-7\]

\[f(x)=3x^2-5x-7\]

Por lo tanto,

• \(a=3\)
• \(b=-5\)
• \(c=-7\)

2. Concavidad

Cuando hablamos de concavidad nos referimos a la «forma» que adopta la grafica, su orientación, es decir, si abre hacia arriba o hacia abajo, por lo tanto, tenemos solo dos opciones:

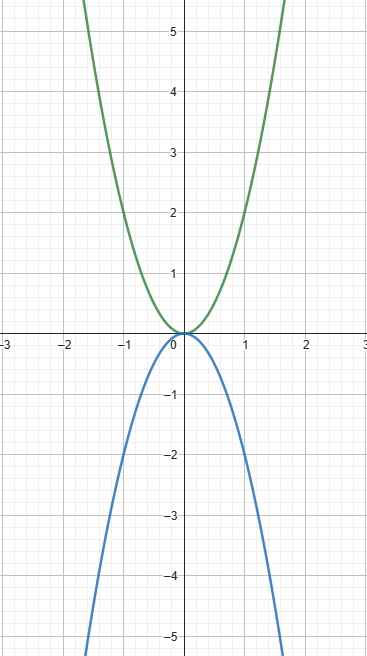
• La parábola verde se obtiene de graficar la función \(f(x)=2x^2\)
• La parábola azul se obtiene de graficar la función \(f(x)=-2x^2\)

Ambas funciones difieren solo en una cosa… el SIGNO del coeficiente \(a\), podemos concluir que:

• Si el coeficiente \(a\) es mayor que 0, es decir \(a>0\) la parábola abre hacia arriba.
• Si el coeficiente \(a\) es menor que 0, es decir \(a<0\) la parábola abre hacia abajo.

Un truco para recordar esto puede ser que, «Si el coeficiente es positivo entonces tendremos una carita feliz (U)», «Si el coeficiente es negativo tendremos una carita triste (∩)».

3. Intercepción con los ejes coordenados

Para determinar las intercepciones (en que punto la gráfica de la función se cruza con el eje) con los ejes tendremos que dividir el trabajo en dos partes. En primer lugar determinar la intercepción con el eje Y (eje de las ordenadas) y en segundo lugar la intercepción con el eje X (eje de las abscisas).

Intercepción con el eje Y

La intercepción con este eje es la más sencilla de encontrar ya que debemos fijarnos en un solo detalle. Entonces si tenemos la función \(f(x)=ax^2+bx+c\), el punto de intercepción de su gráfica con el eje Y será:

\[(0,c)\]

Te lo demuestro de la siguiente manera.

Piensa que tienen en común todos aquellos puntos que pertenecen al eje Y… te ayudo un poco más, los siguientes puntos pertenecen al eje Y, (0,1), (0,2), (0,3), (0,4), (0,5) y bueno descubriste qué es lo que tienen en común?… exacto todos empiezan con un 0, podemos concluir entonces que:

Todos los puntos pertenecientes al eje Y tienen como coordenada X un 0.

Vamos a utilizar esto entonces para determinar el punto de intercepción con el eje Y (que ya te lo dí pero bueno, ahora lo comprobaremos)

Si tenemos \(f(x)=ax^2+bx+c\) y hacemos que \(x=0\) al evaluar (reemplazar la x) obtendremos que:

\[f(0)=a(0)^2+b(0)+c\]

\[f(0)=0+0+c\]

\[f(0)=c\]

Solamente persiste la c, como habíamos dicho inicialmente.

Intercepción con el eje X

En este punto podríamos tener problemas, ya que siguiendo la lógica mostrada anteriormente para determinar los puntos de intercepción con el eje X, debemos hacer que la \(y=0\) obteniendo lo siguiente:

\(f(x)=y=0\), no te olvides que podemos convenientemente cambiar la \(f(x)\) por una \(y\). Esto significa que

\[0=ax^2+bx+c\]

lo anterior es una ecuación cuadrática (puedes ir a revisar mi publicación acerca de este tema). Dentro de esta publicación no ahondaré en los detalles de como se resuelve una ecuación cuadrática, sin embargo, haré un breve resumen.

Para resolver una ecuación cuadrática y poder encontrar estos puntos de intercepción tenemos principalmente dos formas (hay más pero con dos creo que serán suficientes, si la curiosidad te domina, investiga también la completación de cuadrados).

1. Factorizando: este proceso es el que más recomiendo, siempre que se pueda o no sea muy compleja la expresión. (puedes encontrar más de este tema en otra de mis publicaciones)
2. Con la fórmula general: esta fórmula suele ser nuestro salvavidas, pero también, resulta más lenta de trabajar. Te la dejo a continuación.

\[x=\frac{-b±\sqrt{b^2-4ac}}{2a}\]

Con esta fórmula encontrarás dos resultados, un resultado o ninguno, para las primeras dos opciones el resultado de los puntos de intercepción se escribirán:

\[(x_1,0) , (x_2,0)\]

Veamos un ejemplo sencillo (más abajo haremos uno más complicado)

Sea la función \(f(x)=x^2+5x+6\), determinar las intercepciones de su gráfica con los ejes coordenados

• Intercepción con el eje Y: hacemos \(x=0\)

\[f(0)=(0)^2+5(0)+6\]

\[f(0)=6\]

El punto de intercepción sería \((0,6)\)

• Intercepción con el eje X: hacemos \(y=0\)

\[0=x^2+5x+6\]

Factorizando nos queda

\[0=(x+3)(x+2)\]

por lo tanto

\[x+3=0 ∨ x+2=0\]

de esto último se tiene que

\(x_1=-3 \) y \(x_2=-2 \)

finalmente los puntos de intercepción con el eje X serán: \((-3,0)\) y \((-2,0)\)

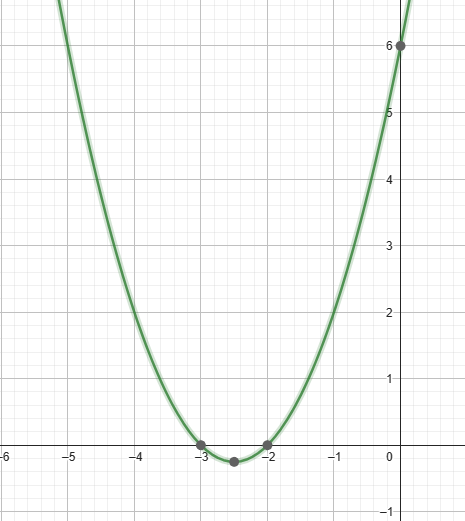
Quizá tienes la siguiente inquietud «pero profe y si la parábola empieza mas arriba o más abajo del eje X, entonces no lo intercepta… y si no lo intercepta, para qué hacemos todo esto? ¿no hay una forma para saber si intercepta antes de hacer todo este proceso?

Muy buena pregunta… sí, la hay, pasemos al siguiente punto.

4. Uso del Discriminante

El discriminante (su símbolo es Δ) aparece en la fórmula general para resolver una ecuación cuadrática (la que acabamos de ver), es la cantidad subradical (que está debajo de la raíz), es decir,

\[Δ=b^2-4ac\]

Este valor puede ser positivo, negativo o cero, en cada uno de esos casos indicará algo distinto.

• Si el \(Δ>0\) entonces la Parábola intercepta al eje X en dos puntos.
• Si el \(Δ=0\) entonces la Parábola intercepta al eje X en un punto.
• Si el \(Δ<0\) entonces la Parábola no intercepta al eje X.

Calculando esto al inicio del problema, podremos evitar en algunas ocasiones (cuando no intercepta) resolver todo el ejercicio.

5. Vértice

El vértice es aquel puntito que identificamos a simple vista, el puntito de más abajo o el de más arriba, dicho con mayor formalidad, el punto mínimo o el punto máximo de nuestra parábola. Que exista un mínimo o un máximo dependerá siempre de la concavidad de la parábola, obviamente, si es hacia arriba tendremos un mínimo y si es hacia abajo tendremos un máximo.

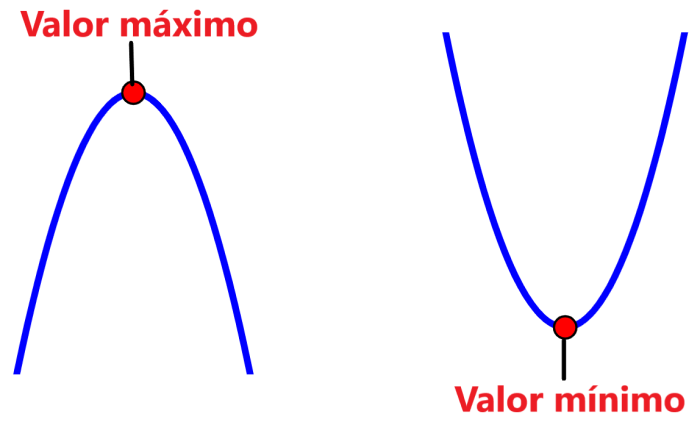
Sin embargo no todo es color de rosas, ya que existe una fórmula más que debemos aprender para determinarlo. Se las compartiré y luego les explicaré (sé que les dará un poco de miedo).

\[V=(\frac{-b}{2a},f(\frac{-b}{2a}))\]

Lo anterior no es la única manera de encontrarlo, sin embargo, es la que más me agrada.

Veamos esto con un ejemplo: «Determinar el vértice o punto mínimo de la función \(f(x)=x^2-6x+8\)»

Paso 1: Identificamos los coeficientes

• \(a=1\)
• \(b=-6\)
• \(c=8\)

Paso 2: Aplicamos la fórmula del vértice

\[V=(\frac{6}{2},f())\]

Explicaciones 😅: cambiamos el signo del -6 pues la fórmula dice \(-b\), dejé en blanco la segunda coordenada pues espero obtener el resultado de la primera y luego reemplazar. Sigamos 🤓.

\[V=(3,f(3))\]

Ahora obtendremos \(f(3)\), para ello reemplazamos el 3 en nuestra función original

\[f(3)=(3)^2-6(3)+8\]

\[f(3)=9-18+8\]

\[f(3)=-9+8\]

\[f(3)=-1\]

Por lo tanto el punto en cuestión (el vértice o el mínimo) es

\[V(3,-1)\]

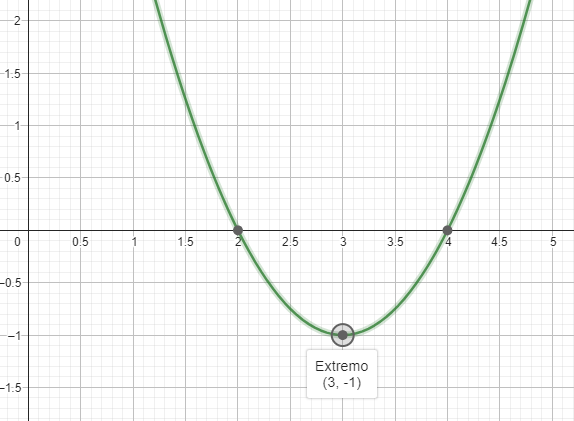
Nota: Si por cosas del destino aún sufres con las sumas de Números Enteros de distintos signos te invito a leer mi publicación acerca del tema.

6. Eje de simetría

Para hablar del eje de simetría, entendamos primeramente que significa que algo sea simétrico, para ello podemos hacernos la idea de un doblez, es decir, si yo puedo doblar algo y las partes resultantes calzan de manera perfecta es porque existe simetría y ese doblez que he realizado sería el eje de simetría. Claramente esto se entenderá mejor con una imagen.

Ahora bien, para la Parábola del ejercicio anterior sería:

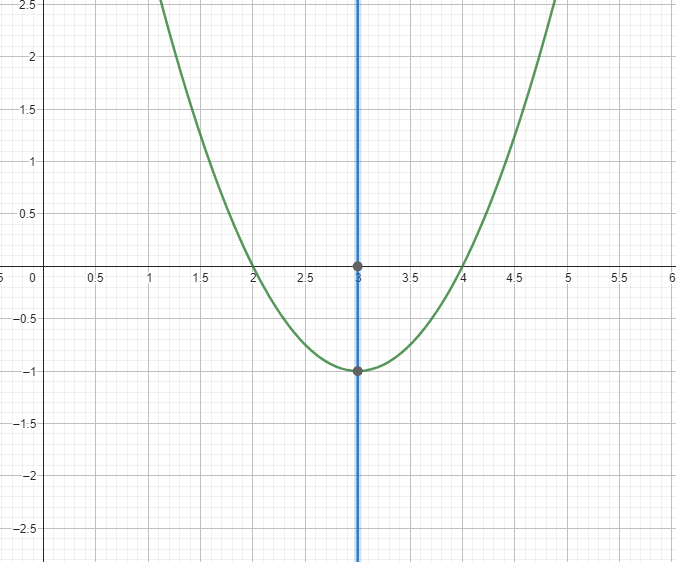
Como ven el eje de simetría es una recta vertical, por lo tanto su ecuación se escribe como \(x=a\).

Como el eje de simetría pasa justo por el vértice, es sencillo determinar su ecuación, ya que coincide con la coordenada x del vértice, por lo tanto, la ecuación del eje de simetría de una parábola es:

\[x=\frac{-b}{2a}\]

Y en el caso de nuestro ejercicio anterior donde \(f(x)=x^2-6x+8\)

• \(x=\frac{-b}{2a}\)
• \(x=\frac{6}{2}\)
• \(x=3\)

Ejemplos resueltos

Ya para ir finalizando este Post, resolveremos algunos ejercicios.

Ejemplo 1: Graficar la función \(f(x)=2x^2+3x-2\)

Solución: Para resolver debemos determinar cada uno de los puntos anteriores.

• Concavidad

El coeficiente \(a=2\), por lo tanto \(a>0\) lo cual indica que la parábola abre hacia arriba.

• Intercepción con los ejes coordenados

Para ver su intercepción con el eje Y, hacemos \(x=0\) y por lo tanto nos queda

\[f(0)=2(0)^2+3(0)-2\]

\[f(0)=-2\]

El punto sería \((0,-2)\)

Si utilizamos el discriminante podremos determinar cuantas intercepciones tiene con el eje X

\[Δ=b^2-4ac\]

\[Δ=(3)^2-4(2)(-2)\]

\[Δ=9+16\]

\[Δ=25>0\]

Como resultó mayor que 0, se concluye que tenemos dos intercepciones.

Para determinar las intercepciones con el eje X, hacemos \(y=0\) y por lo tanto nos queda

\[0=2x^2+3x-2\]

Esta ecuación cuadrática puede ser resuelta factorizando o con la fórmula general, en este caso utilizaremos la fórmula:

\[x=\frac{-b±\sqrt{b^2-4ac}}{2a}\]

Para los coeficientes

• \(a=2\)
• \(b=3\)
• \(c=-2\)

\[x=\frac{-3±\sqrt{(3)^2-4(2)(-2)}}{2(2)}\]

\[x=\frac{-3±\sqrt{9+16}}{4}\]

\[x=\frac{-3±\sqrt{25}}{4}\]

\[x=\frac{-3±5}{4}\]

\(x_1=\frac{-8}{4}\) y \(x_2=\frac{2}{4}\)

\(x_1=-2\) y \(x_2=\frac{1}{2}\)

Por lo que los puntos de intercepción con el eje X son \((-2,0)\) y \((\frac{1}{2},0)\)

• Vértice

Utilizamos la fórmula para obtener este punto.

\[V=(\frac{-3}{2(2)},f(\frac{-3}{2(2)}))\]

\[V=(\frac{-3}{4},f(\frac{-3}{4}))\]

Ahora encontramos \(f(\frac{-3}{4})=2(\frac{-3}{4})^2+3(\frac{-3}{4})-2\)

=\(2(\frac{9}{16})-(\frac{9}{4})-2\)

=\((\frac{9}{8})-(\frac{9}{4})-2\)

=\((\frac{9}{8})-(\frac{18}{8})-\frac{16}{8}\)

=\(\frac{-25}{8}\)

De esta manera el vértice corresponde al punto:

\[V=(\frac{-3}{4},\frac{-25}{8})\]

Equivalentemente sería:

\[V=(-0.75,-3.125)\]

Con estos valores podemos ya esbozar nuestra gráfica:

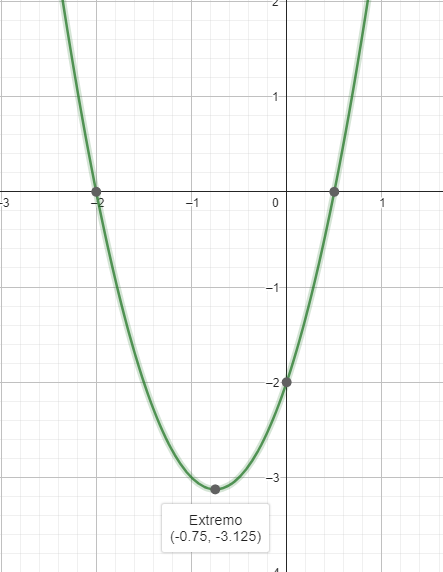
Un detalle importante a considerar es que el eje de simetría nos orienta en el proceso de ubicar los puntos ya que se cumple la simetría, es decir, los puntos de uno de los «brazos» de la parábola se encuentran a la misma distancia respecto del eje que los del otro «brazo»

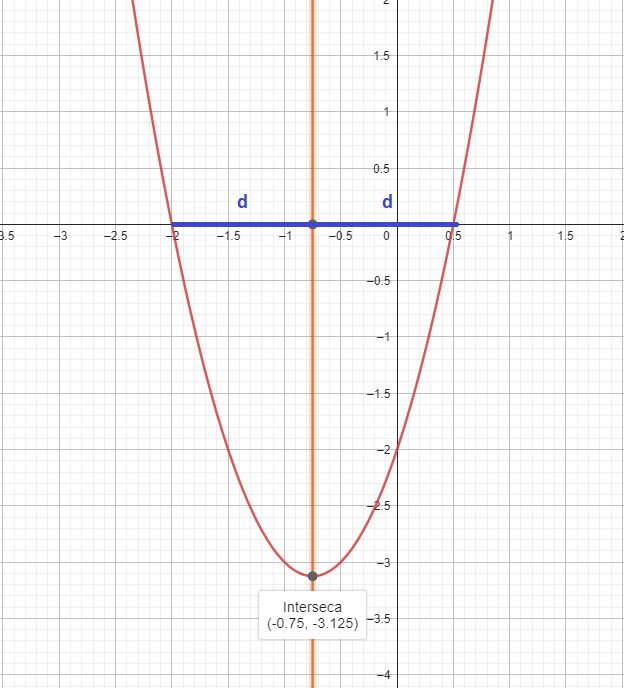
Ejemplo 2: Este ejemplo es tomado directamente de un ensayo PAES

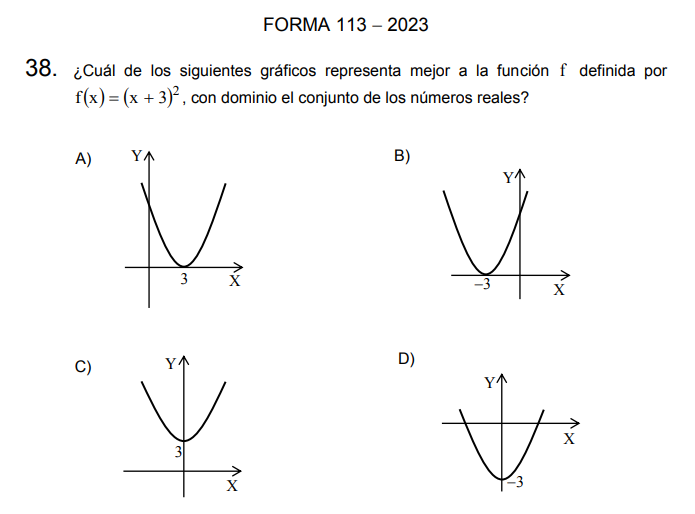
Solución: hasta este punto no hemos hablado acerca de los desplazamientos que sufre la parábola al añadir o quitar coeficientes, sin embargo, procederemos con lo visto anteriormente. Para ello resolveremos el cuadrado de binomio.

\[f(x)=(x+3)^2\]

\[f(x)=x^2+6x+9\]

Sus coeficientes son

• \(a=1\)
• \(b=6\)
• \(c=9\)

Al ver las alternativas se observa que todas tienen un vértice en distintos puntos, por lo cual, si lo calculamos podremos seleccionar inmediatamente la correcta.

\[V=(\frac{-6}{2},f(\frac{-6}{2}))\]

\[V=(-3,f(-3))\]

Calculamos ahora \(f(-3)\)

\[f(-3)=(-3)^2+6(-3)+9\]

\[f(-3)=9-18+9\]

\[f(-3)=0\]

Finalmente el Vértice es \(V=(-3,0)\)

De esta manera la alternativa correcta es la B