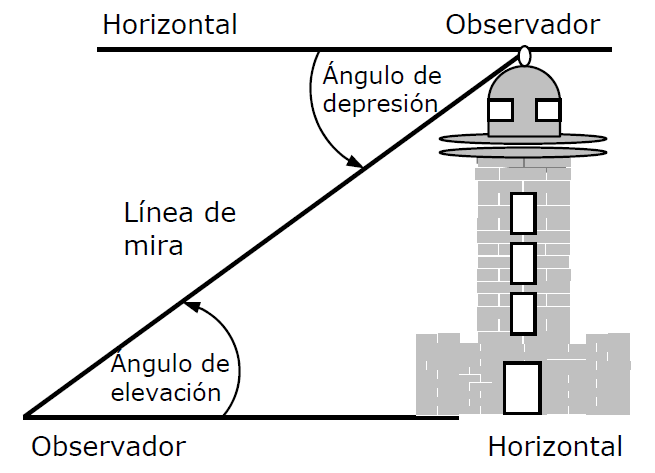
En este espacio hablaremos sobre un tema que relaciona muy fuertemente el Álgebra con la Geometría.
No se confundan las razones trigonométricas, son solo una parte de la Trigonometría.
Trabajaremos con el famoso triángulo rectángulo, pero por si alguien lo olvidó, es el triángulo que tiene un ángulo de 90°.
Las razones trigonométricas relacionan un ángulo con lados específicos del triángulo y por su puesto al hablar de razones, nos referimos a una división o fracción. Empecemos.
Seno
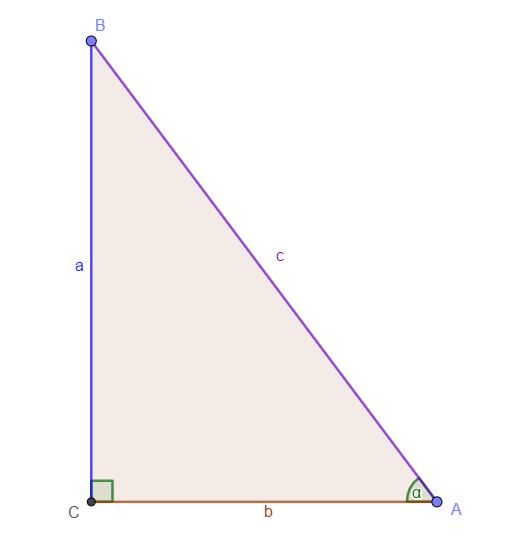
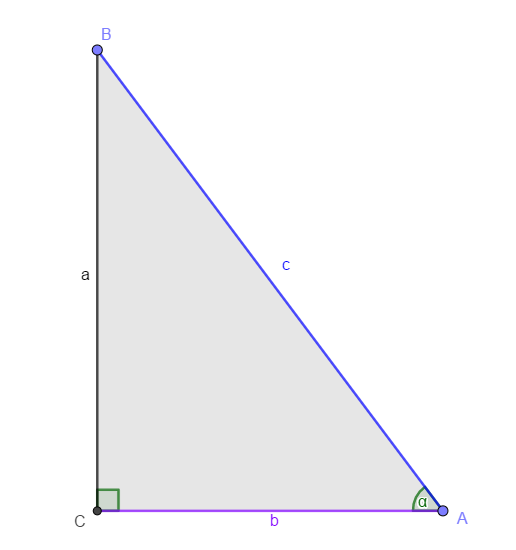
Esta razón relaciona el cateto opuesto al ángulo y la hipotenusa del triángulo, es decir:
\[sen(\alpha)=\frac{Co}{Hip}=\frac{a}{c}\]
Coseno
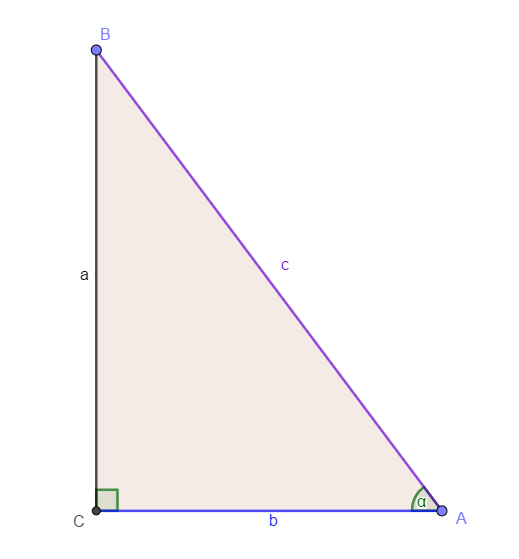
Esta razón relaciona el cateto adyacentes al ángulo y la hipotenusa del triángulo, es decir:
\[cos(\alpha)=\frac{Ca}{Hip}=\frac{b}{c}\]
Tangente
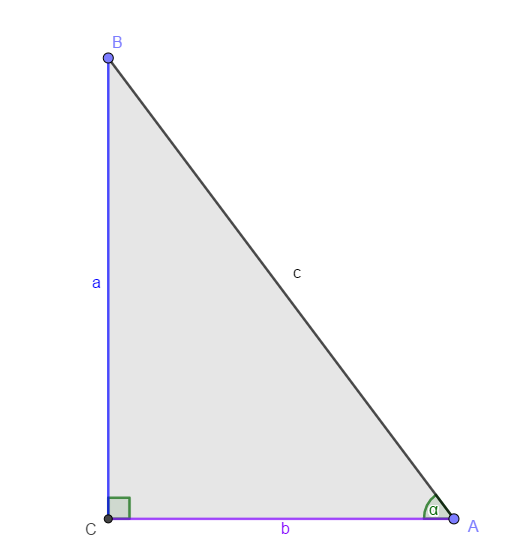
Esta razón relaciona el cateto opuesto al ángulo y su cateto adyacente, es decir:
\[tan(\alpha)=\frac{Co}{Ca}=\frac{a}{b}\]
Cotangente
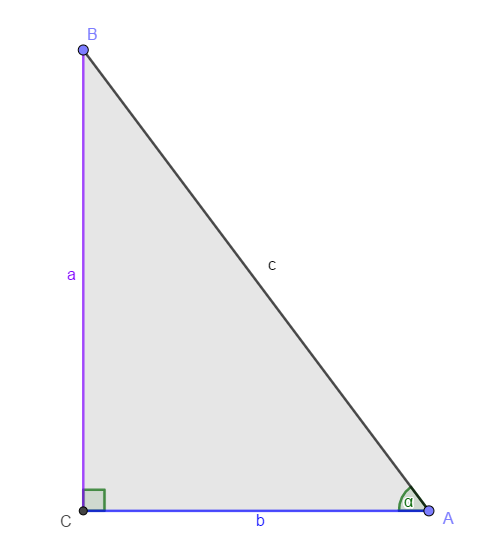
Esta razón relaciona el cateto adyacente al ángulo y su cateto opuesto, es decir:
\[Ctan(\alpha)=\frac{Ca}{Co}=\frac{b}{a}\]
Secante
Esta razón relaciona la hipotenusa del triángulo con su cateto adyacente, es decir:
\[sec(\alpha)=\frac{Hip}{Ca}=\frac{c}{b}\]
Cosecante
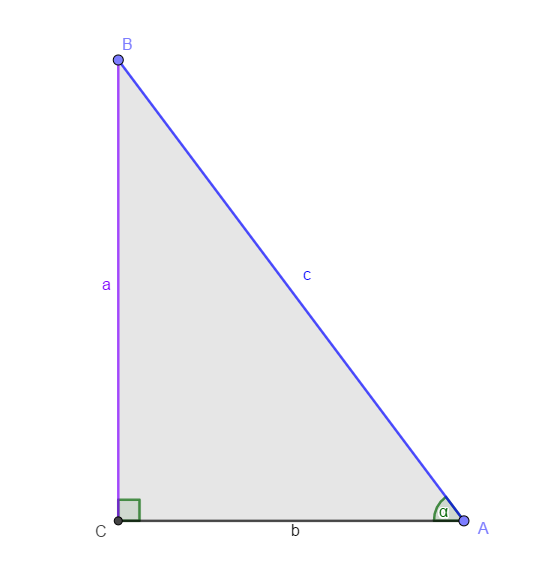
Esta razón relaciona la hipotenusa del triángulo con su cateto opuesto, es decir:
\[Csec(\alpha)=\frac{Hip}{Co}=\frac{c}{a}\]
Método del «borrachito»
El nombre quizá no gusta mucho pero es una forma de recordar todas las fórmulas.
Paso 1: escribimos el nombre de cada una de las razones en una columna:
\(sen(\alpha)=\)
\(cos(\alpha)=\)
\(tan(\alpha)=\)
\(Ctan(\alpha)=\)
\(sec(\alpha)=\)
\(Csec(\alpha)=\)
Paso 2: completamos todos los numeradores de las fracciones con las palabras, co-ca-co-ca-hip-hip
\(sen(\alpha)=\frac{co}{}\)
\(cos(\alpha)=\frac{ca}{}\)
\(tan(\alpha)=\frac{co}{}\)
\(Ctan(\alpha)=\frac{ca}{}\)
\(sec(\alpha)=\frac{hip}{}\)
\(Csec(\alpha)=\frac{hip}{}\)
Paso 3: completamos todos los denominadores con la misma secuencia, pero de abajo hacia arriba
\(sen(\alpha)=\frac{co}{hip}\)
\(cos(\alpha)=\frac{ca}{hip}\)
\(tan(\alpha)=\frac{co}{ca}\)
\(Ctan(\alpha)=\frac{ca}{co}\)
\(sec(\alpha)=\frac{hip}{ca}\)
\(Csec(\alpha)=\frac{hip}{co}\)
Importante: podemos obtener variadas combinaciones adicionales por ejemplo:
\[tan(x)=\frac{sen(x)}{cos(x)}\]
\[tan(x)=\frac{\frac{co}{hip}}{\frac{ca}{hip}}\]
\[tan(x)=\frac{co}{hip}\cdot\frac{hip}{ca}\]
\[tan(x)=\frac{co}{ca}\]
otro ejemplo puede ser:
\[\frac{1}{sen(x)}=\frac{1}{\frac{co}{hip}}\]
\[\frac{1}{sen(x)}=1\cdot\frac{hip}{co}\]
\[\frac{1}{sen(x)}=\frac{hip}{co}\]
\[\frac{1}{sen(x)}=Csec(x)\]
Después de estos truquitos revisaremos el último contenido antes de los ejercicios resueltos. Esto no quiere decir que no se pueda profundizar más en la trigonometría… espero que les llame la atención y puedan seguir investigando.
Razones trigonométricas para «Ángulos Notables»
Bien, reconozco que inventé el nombre, pero quiero referirme a cuando utilizamos razones trigonométricas para algunos ángulos especiales, estos ángulos son 30°, 45° y 60°.
Veamos el de 30°, para esto trabajaremos con un viejo amigo, el triángulo equilátero:
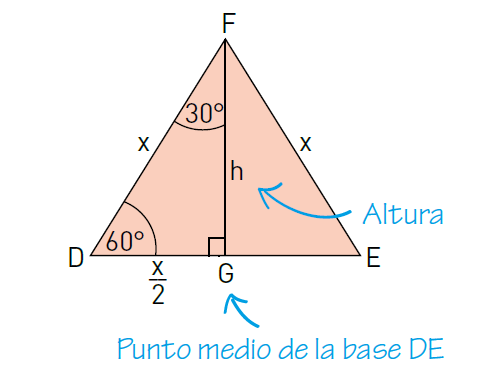
Recordemos algunas cositas, en un triángulo equilátero todos los lados miden lo mismo (x), además, todos los elementos secundarios coinciden (altura, bisectriz y transversal de gravedad), sus ángulos miden 60° y bueno algunas cosas más… esto de los elementos secundarios nos ayudará, en el dibujo aparece la altura (h), la cual coincide con la bisectriz (por eso el ángulo mide 30° ya que la bisectriz divide al ángulo en dos de igual medida) y con la transversal de gravedad (esta divide al lado opuesto al vértice desde donde se origina en dos partes iguales, por esta razón el segmento DG mide \(\frac{x}{2}\) ).
Ahora sin perdernos vamos a utilizar el Teorema de Pitágoras para obtener la medida de la altura (h)
\[h^2+(\frac{x}{2})^2=x^2\]
Claramente de esta expresión debemos despejar la h
\[h^2=x^2-(\frac{x}{2})^2\]
\[h^2=x^2-\frac{x^2}{4}\]
\[h^2=\frac{4x^2}{4}-\frac{x^2}{4}\]
\[h^2=\frac{4x^2-x^2}{4}\]
\[h^2=\frac{3x^2}{4}\]
estamos casi casi, lo que nos falta es eliminar el exponente de h, para ello sacaremos raíz cuadrada en ambos lados.
\[\sqrt{h^2}=\sqrt{\frac{3x^2}{4}}\]
\[h=\frac{\sqrt{3x^2}}{\sqrt{4}}\]
\[h=\frac{\sqrt{3}x}{2}\]
lo conseguimos!
con todos los valores podremos calcular las distintas razones trigonométricas asociadas al ángulo de 30°.
\[sen(30°)=\frac{\frac{x}{2}}{x}\]
\[sen(30°)=\frac{x}{2}\cdot\frac{1}{x}\]
\[sen(30°)=\frac{1}{2}\]
listo el seno, vamos ahora por coseno
\[cos(30°)=\frac{\frac{\sqrt{3}x}{2}}{x}\]
\[cos(30°)=\frac{\sqrt{3}x}{2}\cdot\frac{1}{x}\]
\[cos(30°)=\frac{\sqrt{3}}{2}\]
por último veremos tangente de 30°
\[tan(30°)=\frac{\frac{x}{2}}{\frac{\sqrt{3}x}{2}}\]
\[tan(30°)=\frac{x}{2}\cdot\frac{2}{\sqrt{3}x}\]
\[tan(30°)=\frac{1}{\sqrt{3}}\]
Si racionalizamos nos quedaría
\[tan(30°)=\frac{1\cdot\sqrt{3}}{\sqrt{3}\cdot\sqrt{3}}\]
\[tan(30°)=\frac{\sqrt{3}}{3}\]
LISTO, repitamos el proceso para el ángulo de 60°
\[sen(60°)=\frac{\frac{\sqrt{3}x}{2}}{x}\]
\[sen(60°)=\frac{\sqrt{3}x}{2}\cdot\frac{1}{x}\]
\[sen(60°)=\frac{\sqrt{3}}{2}\]
listo el seno, vamos ahora por coseno
\[cos(60°)=\frac{\frac{x}{2}}{x}\]
\[cos(60°)=\frac{x}{2}\cdot\frac{1}{x}\]
\[cos(60°)=\frac{1}{2}\]
finalmente vamos por tangente
\[tan(60°)=\frac{\frac{\sqrt{3}x}{2}}{\frac{x}{2}}\]
\[tan(60°)=\frac{\sqrt{3}x}{2}\cdot\frac{2}{x}\]
\[tan(60°)=\sqrt{3}\]
si se pudo… nos falta el ángulo de 45°, para plantear las razones debemos cambiar de triángulo ya que en el querido equilátero no tenemos ángulos de esta medida.
usaremos un triángulo rectángulo isósceles (tiene un ángulo de 90° y sus catetos de igual medida, esto último implica que los dos ángulos restantes miden lo mismo, 45°)
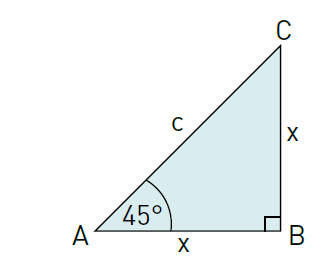
Lo primero es determinar la medida de la hipotenusa c, para esto usaremos nuevamente el Teorema de Pitágoras
\[c^2=x^2+x^2\]
\[c^2=2x^2\]
\[c=\sqrt{2x^2}\]
\[c=\sqrt{2}x\]
con esta medida lista podemos encontrar las razones trigonométricas, sigamos el mismo orden anterior
\[sen(45°)=\frac{x}{\sqrt{2}x}\]
\[sen(45°)=\frac{1}{\sqrt{2}}\]
si racionalizamos nos queda
\[sen(45°)=\frac{1\cdot\sqrt{2}}{\sqrt{2}\cdot\sqrt{2}}\]
\[sen(45°)=\frac{\sqrt{2}}{2}\]
listo el seno vamos con coseno
\[cos(45°)=\frac{\sqrt{2}}{2}\]
ups! Fue muy rápido ya que las medidas son las mismas (isósceles).
finalmente tendremos la tangente
\[tan(45°)=\frac{x}{x}\]
\[tan(45°)=1\]
Ahora sí que sí, vamos por los ejercicios resueltos y terminamos este post.
Ejercicios resueltos
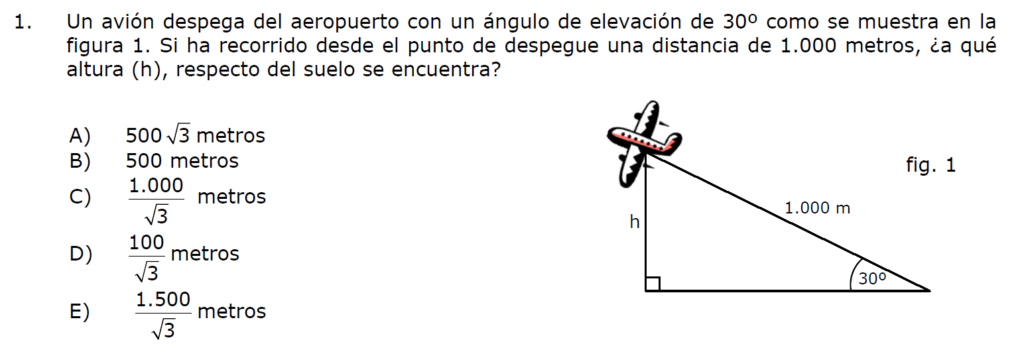
Desarrollo:
Se nos pide encontrar la altura (h), se nos da el ángulo de elevación (en la siguiente imagen pueden verlo en detalle) y la medida de la hipotenusa.
ahora debemos pensar en lo que tenemos y lo que nos falta, la altura es el cateto opuesto al ángulo por lo que la razón trigonométrica a utilizar debe ser Seno, es decir,
\[sen(30°)=\frac{h}{1000}\]
Recuerden que \(sen(30°) = \frac{1}{2}\), por lo que
\[\frac{1}{2}=\frac{h}{1000}\]
Terminemos de despejar la altura (h)
\[\frac{1}{2}=\frac{h}{1000}\]
\[\frac{1\cdot1000}{2}=h\]
\[\frac{1000}{2}=h\]
\[500=h\]
por lo tanto el avión ✈️ se encuentra a 500 metros de altura.
Con esto claro veamos otro ejemplo.

Desarrollo:
en esta ocasión nos dan el ángulo (40°), el cateto opuesto (altura del edificio) y nos piden hallar el cateto adyacente (sombra), por lo tanto, debemos usar la razón trigonométrica Tangente.
\[tan(40°)=\frac{50}{sombra}\]
en este caso no sabemos exactamente cuánto es el tan(40°), sin embargo, no lo necesitamos puesto que las alternativas piden dejarlo expresado. Despejemos la sombra.
\[tan(40°)=\frac{50}{sombra}\]
\[tan(40°)\cdot sombra=50\]
\[sombra=\frac{50}{tan(40°)}\]
la alternativa correcta es la C.

Desarrollo:
nos cambian un poco la figura, sin embargo, debemos enfocarnos en el triángulo superior. A la altura total (21,5) le restamos la altura de la persona (1,5) este resultado es la medida del cateto opuesto al ángulo de 45°.
La medida del hilo es la hipotenusa del triángulo por lo que la razón trigonométrica a utilizar es Seno.
\[sen(45°)=\frac{21,5-1,5}{hilo}\]
\[sen(45°)=\frac{20}{hilo}\]
\[sen(45°)\cdot hilo=20\]
\[hilo=\frac{20}{sen(45°)}\]
Más arriba vimos que \(sen(45°)=\frac{\sqrt{2}}{2}\), por lo que
\[hilo=\frac{20}{\frac{\sqrt{2}}{2}}\]
\[hilo=20\cdot\frac{2}{\sqrt{2}}\]
\[hilo=\frac{40}{\sqrt{2}}\]
si racionalizamos queda
\[hilo=\frac{40\sqrt{2}}{\sqrt{2}\cdot{\sqrt{2}}}\]
\[hilo=\frac{40\sqrt{2}}{2}\]
\[hilo=20\sqrt{2}\]
la alternativa correcta es la A.
