Traigo para ustedes otro contenido clásico del eje Datos y Azar, las famosas Medidas de tendencia central (MTC), como su nombre lo indica, medidas que tienden a estar ubicadas en el centro de una distribución.
Las MTC son la Media (promedio), la Moda y la Mediana, voy a darles una pequeña explicación de cada una antes de abordar las fórmulas y los ejemplos.
La media (\(\bar{x}\)): creo que de todas, esta puede ser la más conocida con su «sinónimo» promedio, todos nos hemos preguntado alguna vez: «Si tengo un 2, un 3 y un 4 ¿Qué nota necesito para tener promedio 6?».
La mediana: la mediana es el hermano del medio, el dato que se encuentra justo en la mitad de todos, pudiera darse que se tiene una cantidad par de datos, en esta situación, la mediana se encontraría entre los dos datos centrales (el promedio de los datos centrales).
La moda: la moda es aquel dato que más se repite, aquel tiene mayor frecuencia absoluta.
Vamos ahora con un poco más de rigor 😎.
Debemos hacer una diferencia entre datos agrupados (aquellos que aparecen en intervalos) y no agrupados, iniciaremos con los no agrupados ya que son mucho más fáciles de obtener.
Medidas de tendencia central para datos no agrupados
Supongamos que un estudiante tiene las siguientes notas
\[3, 4, 5, 7, 2, 1, 4, 3\]
La media: sumamos todos los datos y los dividimos en la cantidad total de datos (\(n\))
\[\frac{3+4+5+7+2+1+4+3}{8}\]
\[\frac{29}{8}=3,6\]
La mediana: ordenamos los datos de menor a mayor
\[1, 2, 3, 3, 4, 4, 5, 7\]
tenemos 8 datos, una cantidad par, por lo tanto la mediana se encuentra entre los dos datos centrales (el dato en la posición 4 y el dato en la posición 5).
\[1, 2, 3, |3, 4|, 4, 5, 7\]
por lo tanto debemos obtener el promedio entre el 3 y el 4 (la mitad entre ellos).
\[\frac{3+4}{2}=\frac{7}{2}=3.5\]
La mediana es 3.5
La moda: La moda es el dato que más se repite, podemos tener una moda, ninguna moda o más de una moda.
En nuestro caso tendremos dos modas: 3 y 4.
Ya que ambos comparten las frecuencias absolutas más altas (ambos salen repetidos 2 veces).
Medidas de tendencia central para datos no agrupados en una tabla de frecuencia
Veremos ahora como obtener las MTC a partir de una tabla de frecuencias.
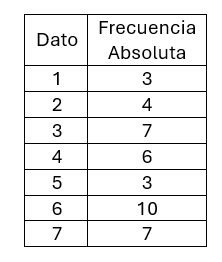
Dada la tabla anterior, debemos obtener la Media, la mediana y la Moda.
La media: Podemos entender la tabla como «3 personas obtuvieron un 1», «4 personas obtuvieron un 2», «7 personas obtuvieron un 3» y así. La media sigue siendo la suma de todos los valores, divididos en el total de datos, solo que en este caso, toda la información está resumida en una tabla.
El total de datos se obtiene sumando todas las frecuencias absolutas:
\[n=3+4+7+6+3+10+7=40\]
Son 40 en total.
La suma de todos los datos, la obtendremos al ir multiplicando «dato por frecuencia» y sumando estos resultados:
\[1\cdot 3 + 2\cdot 4 + 3\cdot 7 + 4\cdot 6 + 5\cdot 3 + 6\cdot 10 + 7\cdot 7 =\]
\[3+8+21+24+15+60+49=\]
\[180\]
La media será:
\[\bar{x}=\frac{180}{40}\]
\[\bar{x}=4.5\]
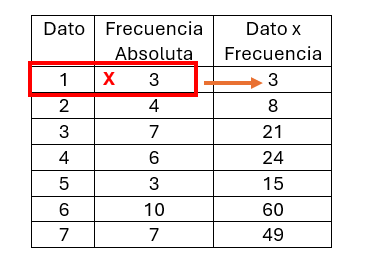
También se puede añadir una columna extra a la tabla con los resultados de las multiplicaciones para luego sumarlas:
La moda: En este caso basta mirar la frecuencia absoluta mayor, con esto determinamos la moda.
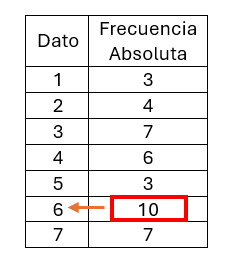
La moda sería 6.
La mediana: Para hallarla, debemos determinar en que posición se encuentra. Tenemos 40 datos, una cantidad par, por lo tanto, la mediana se encuentra entre los datos 20 y 21.
Para encontrarla más fácilmente, podemos añadir la columna de frecuencia absoluta acumulada y a partir de ella encontrar los datos solicitados.

El dato 20 se encuentra en la cuarta fila y el dato 21 en la quinta, estos son los casos mas complejos, nos tocará obtener el promedio entre 4 y 5. En otras ocasiones los datos buscados (20 y 21) estarán en una misma fila y solo nos remitiremos a mirar el valor del dato. (veremos más ejemplos)
Mediana: \(\frac{4+5}{2}=4.5\)
Medidas de tendencia central para datos agrupados
Vamos a calcular nuevamente las tres medidas de tendencia central pero esta vez con una tabla de datos agrupados.
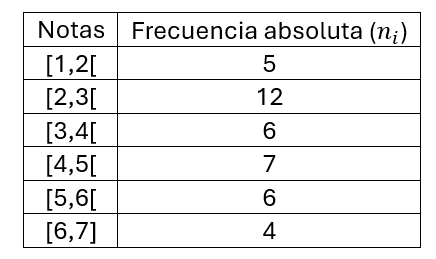
En la tabla de frecuencias anterior aparecen las notas agrupadas por intervalos, de 1 a 2, 2 a 3 y así, los paréntesis indican por ejemplo que en [1,2[ tenemos todas las notas mayores o iguales a 1 pero menores que 2, las notas 2 se ubican en la segunda fila.
Tenemos en total 40 notas, es decir, \(n=40\).
Media: Vamos a dejar la fórmula de la media a modo de referencia, sin embargo, planeo enseñarles a calcularla a través de la tabla.
\[\bar{x}=\frac{1}{n}\cdot \sum_{i=1}^{k} x_{mci}\cdot n_i\]
En palabras sencillas, la fórmula indica que debemos sumar todos los resultados de multiplicar la marca de clase de cada intervalo (\(x_{mci}\)) por su respectiva frecuencia absoluta (\(n_i\)) y luego dividir este resultado en la cantidad total de datos (\(n\)).
Yo realizaré lo equivalente por medio de la tabla, pero antes les explicaré qué es la «marca de clase».
Marca de clase \(x_{mci}\): Es el promedio entre el limite inferior y superior de cada intervalo. Si miramos el intervalo de la primera fila dice: [1,2[ el límite inferior sería 1 y el superior 2 (de izquierda a derecha), en otras palabras «la mitad del intervalo». Si añadimos una columna con todos estos valores tendremos:

Ahora, añadimos una nueva columna con los resultados de multiplicar las frecuencias absolutas por sus marcas de clase:
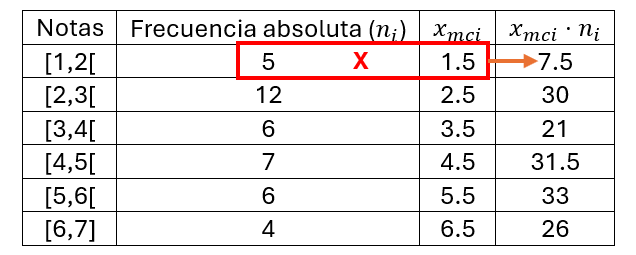
El siguiente paso es sumar todos estos resultados
\[7.5+30+21+31.5+33+26=149\]
Finalmente dividimos este resultado en la cantidad total de datos (40)
\[\bar{x}=\frac{149}{40}=3.7\]
Mediana: Antes de escribir la fórmula para obtener la mediana, debemos determinar en que intervalo se encuentra, para ello añadiremos la frecuencia absoluta acumulada y teniendo en consideración que son 40 datos en total, la mediana debe estar entre el dato 20 y 21.

El intervalo destacado es el que contiene a la mediana.
\[\text{mediana}=L_i + \frac{\frac{n}{2}-N_{i-1}}{n_i}\cdot a\]
- \(n\): cantidad total de datos
- \(L_i\): límite inferior.
- \(N_i\): frecuencia absoluta acumulada del intervalo anterior.
- \(n_i\): frecuencia absoluta del intervalo.
- \(a\): amplitud del intervalo (Límite superior menos Límite inferior).
Reemplazamos nuestros datos y calculamos
\[\text{mediana}=3 + \frac{\frac{40}{2}-17}{6}\cdot 1\]
\[\text{mediana}=3 + \frac{3}{6}\cdot 1\]
\[\text{mediana}=3 + 0.5\]
\[\text{mediana}=3.5\]
La mediana nos dio 3.5 lo cual además tiene lógica ya que el valor se ubica en el intervalo que seleccionamos.
Moda: La moda, al igual que la mediana, cuenta con su fórmula, y a su vez debemos determinar el intervalo que la contiene (aquel que tiene mayor frecuencia absoluta).
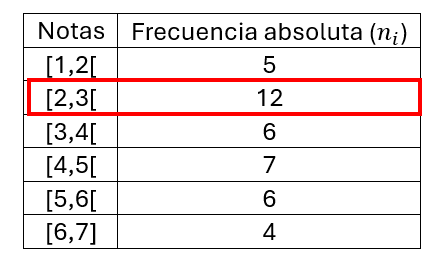
\[\text{moda}=L_i + \frac{D_1}{D_1+D_2}\cdot a\]
- \(D_1\): frecuencia absoluta del intervalo modal menos la del intervalo anterior
- \(D_2\): frecuencia absoluta del intervalo modal menos la del intervalo siguiente
- \(a\): amplitud del intervalo (Límite superior menos Límite inferior).
Reemplazamos nuestros datos y calculamos
\[\text{moda}=2 + \frac{7}{7+6}\cdot 1\]
\[\text{moda}=2 + \frac{7}{13}\cdot 1\]
\[\text{moda}=2 + 0.54\cdot 1\]
\[\text{moda}=2.54\]
Solo nos resta ver algunos ejercicios resueltos tipo PAES.
Ejercicios resueltos
Intentaré subir las resoluciones en estos días.
Dejo un saludo para Danna que me animó bastante a subir este post!
